指示器随机变量

算法导论课程中，老师在介绍随机算法的时候提到指示器随机变量（indicator random variable），感觉很有用的一个东东。

先介绍一下指示器随机变量。

给定一个样本空间S和 事件A，那么事件A对应的指示器随机变量I{A}=1（如果A发生），0（如果A不发生）；

显而易见，事件A对应的指示器随机变量的期望等于事件A发生的概率。

举一个简单的例子：连续抛硬币n次，计算正面朝上的期望次数。

对此,有种显而易见的解法就是依次计算n次抛硬币中有1……n个硬币朝上的概率，然后根据离散型随机变量期望的定义（要求级数收敛）

求出期望，但是，显而易见，这样做工作量是个问题。

下面用指示器随机变量的思路解决这个问题：

可知:

 

可见指示器随机变量极大地简化了操作。

个人感觉，指示器随机变量的功用在于将一个大的问题拆分为n个比较简单的随机变量之和，然后通过计算这些简单的随机变量的数学期望，进而求和得出原问题的数学期望。有点类似分治法的意思。

为了熟练使用指示器随机变量，下面给出几个题目。

有n位顾客，他们每个人给餐厅负责保管帽子的服务生一顶帽子。服务生以随机的顺序将帽子归还给顾客。请问拿到自己帽子的顾客的期望数量是多少？

 

可以先想想怎么使用再看答案：

提示：

 

对于每个顾客而言，拿到自己的帽子的概率为

，

　　2. 假设A[n]为由n个不同的数随机组成的数组，计算A[n]中逆序对个数的数学期望？

提示：

 

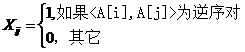
　　3. R个人在楼的底层进入电梯，楼上有n层，每个乘客在任一楼层下电梯的概率相同。如果到某一层无乘客下电梯则电梯不停，求直到乘客都下完时电梯停车次数的数学期望。

提示：

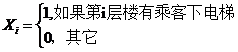
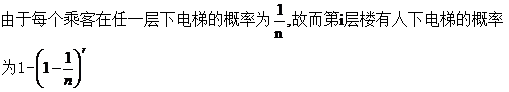
总结：上面给出的三个典型例子，如果直接用期望定义去做，运算复杂度很高甚至于难以解决，但是，指示器随机变量的引入使得我们很方便的做出了这些个问题。

 

转自: 苯苯吹雪  http://www.cnblogs.com/xubenben/archive/2012/12/18/2823098.html