空洞卷积

参考：https://www.cnblogs.com/houjun/p/10275215.html

https://www.jianshu.com/p/f743bd9041b3

一、含义

空洞卷积是在标准的卷积核里注入空洞，以此来增加感受野/接受域。相比原来的正常卷积运算，空洞卷积 多了一个 超参数称之为 dilation rate 指的是kernel的间隔数量(e.g. 正常的 convolution 是 dilatation rate 1)。

 

空洞卷积

 

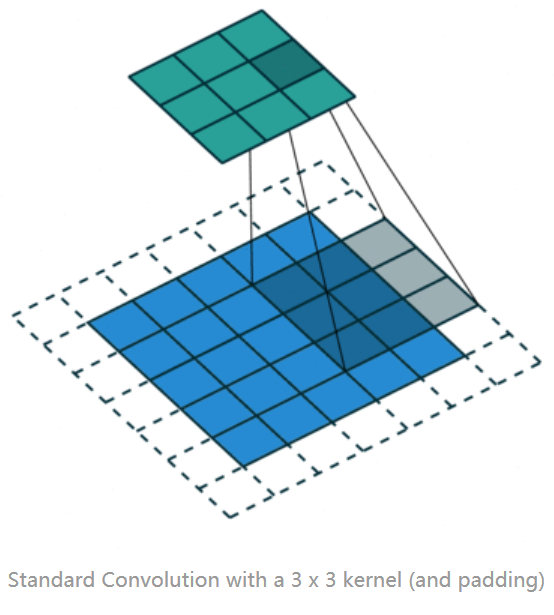
正常卷积运算

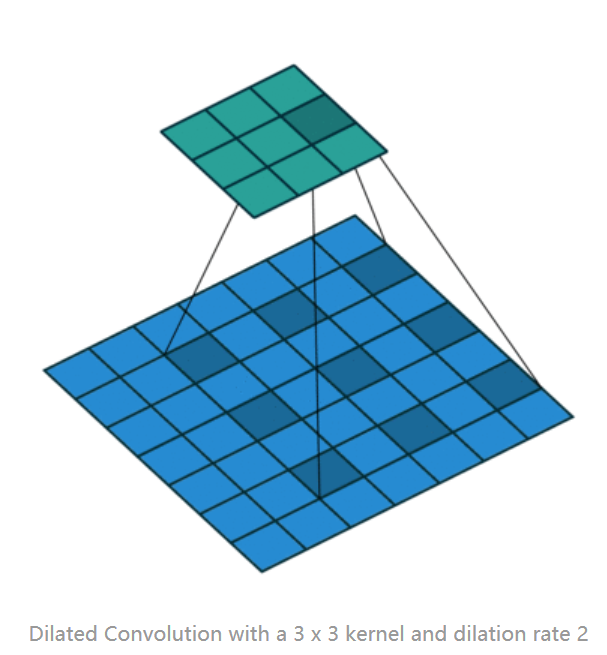
 二、提出的原因

Deep CNN 对于其他任务还有一些致命性的缺陷。较为著名的是 up-sampling 和 pooling layer 的设计。
主要问题有：

1、Up-sampling / pooling layer (e.g. bilinear interpolation) is deterministic. (参数不可学习)

2、内部数据结构丢失；空间层级化信息丢失。

3、小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)
在这样问题的存在下，语义分割问题一直处在瓶颈期无法再明显提高精度， 而 dilated convolution 的设计就良好的避免了这些问题。

 

三、膨胀卷积的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。在图像需要全局信息或者自然语言处理中需要较长的sequence信息依赖的问题中，都能很好的应用。

tf.nn.atrous_conv2d(value,filters,rate,padding,name=None）

　　value：输入的卷积图像，[batch, height, width, channels]。

   　 filters：卷积核，[filter_height, filter_width, channels, out_channels]，通常NLP相关height设为1。

　　rate：正常的卷积通常会有stride，即卷积核滑动的步长，而膨胀卷积通过定义卷积和当中穿插的rate-1个0的个数，实现对原始数据采样间隔变大。

　　padding：”SAME”：补零   ； ”VALID”：丢弃多余的

膨胀后的卷积核尺寸：

膨胀的卷积核尺寸 = 膨胀系数 * (原始卷积核尺寸 - 1) + 1

kd = k +（k-1）·（r-1），其中kd是膨胀后的卷积核大小，k是原卷积核大小，r是膨胀系数

膨胀卷积感受野：

[(n-1)*(ksize+1)+ksize]×[(n-1)*(ksize+1)+ksize]，n = 膨胀系数

空洞卷积的叠加感受野计算方法，下面来介绍一下空洞卷积的感受野变化（卷积核大小为 ，stride=1，下面的卷积过程后面的以前面的为基础）：

1-dilated conv：rate=1的卷积其实就是普通 因此 （ ）卷积因此感受野为

2-dilated conv：rate=2可以理解为将卷积核变成了 ，因此 （ ）感受野大小为 。

4-dilated conv：rate=4可以理解为将卷积核变成了 因此 （ ）感受野大小为 15×15

可以看到将卷积以上面的过程叠加感受野变化会指数增长，感受野公式为 2ⁱ⁺²−1，for i = 0,1,2,3,4

 

四、空洞卷积工作原理

二维

(a)图对应3x3的1-dilated conv，和普通的卷积操作一样，(b)图对应3x3的2-dilated conv，实际的卷积kernel size还是3x3，但是空洞为1，也就是对于一个7x7的图像patch，

只有9个红色的点和3x3的kernel发生卷积操作，其余的点略过。也可以理解为kernel的size为7x7，但是只有图中的9个点的权重不为0，其余都为0。 可以看到虽然kernel size只有3x3，

但是这个卷积的感受野已经增大到了7x7（如果考虑到这个2-dilated conv的前一层是一个1-dilated conv的话，那么每个红点就是1-dilated的卷积输出，所以感受野为3x3，

所以1-dilated和2-dilated合起来就能达到7x7的conv）,(c)图是4-dilated conv操作，同理跟在两个1-dilated和2-dilated conv的后面，能达到15x15的感受野。

对比传统的conv操作，3层3x3的卷积加起来，stride为1的话，只能达到(kernel-1)*layer+1=7的感受野，也就是和层数layer成线性关系，而dilated conv的感受野是指数级的增长。

a,b,c三张图都是以前面结果为基础，a的感受野是3x3，b以a图进行卷积，b本身感受野为5x5（以原图进行卷积，图b示黑色正方形区域）加上以a的3x3感受野变成7x7，即，b图的红点对应a图的卷积结果，对应原图9x9像素。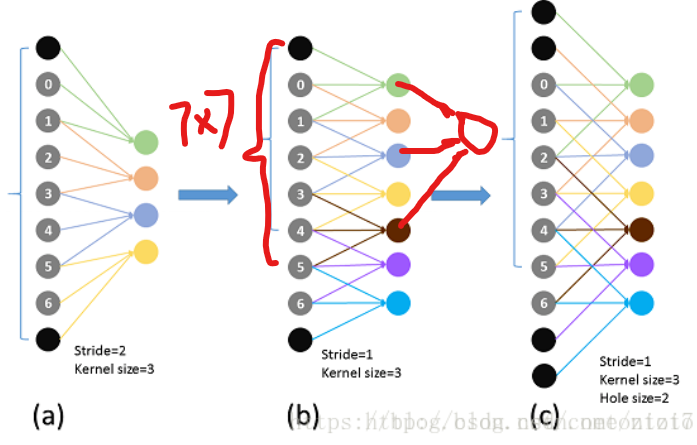

一维

(a)为k=3，stride=2 的普通卷积；(b)为k=3，stride=1的卷积；(c)为k=3，stride=1，dilation=2的空洞卷积，这里虽然卷积核长度仍为3，但每隔2个点采样一次（也可以理解为长度为5但其中两个位置权重为0）

以一维图b红色笔所示k=3，stride=1，dilation=1的卷积 + k=3，stride=1，dilation=2的空洞卷积之后每个feature maps像素对应叠加感受野是7x7。同理二维也一样。
五、问题

1、格网问题

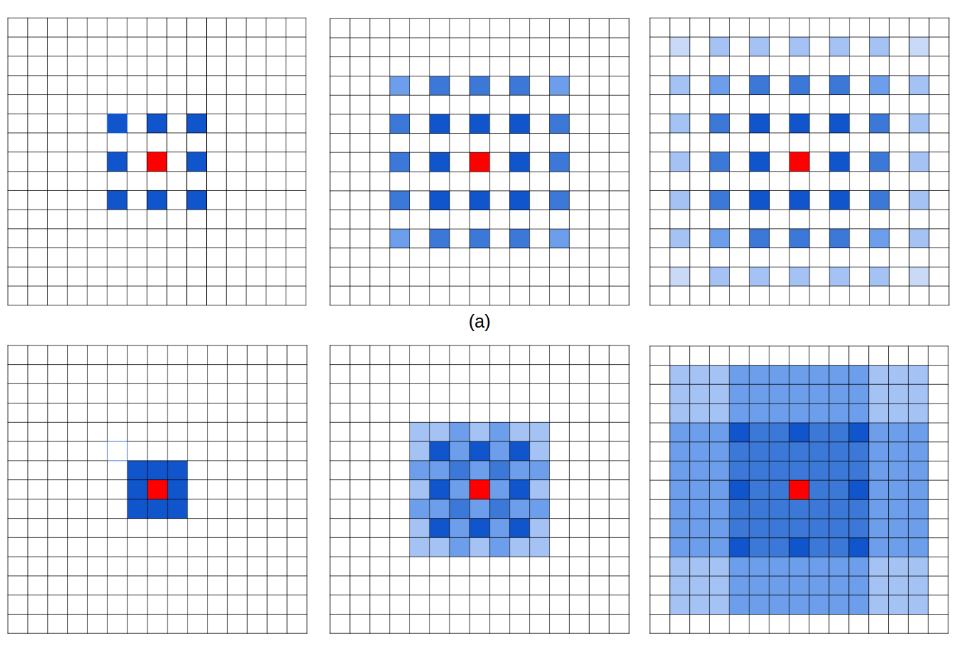
图2.网格问题的图示。 从左到右：像素（用蓝色标记）有助于通过三个内核大小为3×3的卷积层计算中心像素（用红色标记）。 （a）所有卷积层都具有膨胀率= 2.（b）随后的卷积层的膨胀率分别为r = 1,2,3。

我们发现我们的 kernel 并不连续，也就是并不是所有的 pixel 都用来计算了，因此这里将信息看做 checker-board 的方式会损失信息的连续性。这对 pixel-level dense prediction 的任务来说是致命的。

我们将其称为“网格化”（图2）：对于空洞卷积层L中的像素p，对像素p有贡献的信息来自来自以p为中心的层L-1中的附近kd×kd区域。。由于扩张卷积在卷积核中引入零，因此从kd×kd区域参与计算的实际像素仅为k×k，

它们之间的间隙为r-1。如果k = 3，r = 2，则该区域中仅25个像素中的9个用于计算（图2（a））。由于所有层具有相等的膨胀率r，那么对于顶部扩张卷积层L中的像素p，有助于计算p值的最大可能位置数是（w'×h'）/ r²

其中w' ，h'分别是底部扩张卷积层的宽度和高度。结果，像素p只能以棋盘方式查看信息，并且在信息中丢失大部分（当r = 2时至少75％）。当由于额外的下采样操作而在较高层中变大时，来自输入可能非常稀疏，

这可能不利于学习，因为1）本地信息完全丢失; 2）信息可能在很远的距离上无关紧要。网格效应的另一个结果是第L层的r×r区域附近的像素从完全不同的“网格”集接收信息，这可能损害本地信息的一致性。

2、Long-ranged information might be not relevant.

我们从 dilated convolution 的设计背景来看就能推测出这样的设计是用来获取 long-ranged information。然而光采用大 dilation rate 的信息或许只对一些大物体分割有效果，而对小物体来说可能则有弊无利了。

如何同时处理不同大小的物体的关系，则是设计好 dilated convolution 网络的关键。

六、解决办法-通向标准化设计：Hybrid Dilated Convolution (HDC)
在这里，我们提出一个简单的解决方案 - 混合扩张卷积（HDC），以解决这个理论问题。 假设我们有N个卷积层，内核大小为K×K，扩展率为[r1，...，ri，...，rn]，HDC的目标是让一系列卷积运算的感受野的最终大小完全覆盖一个正方形 区域没有任何孔或缺少边缘。

第一个特性是，叠加卷积的 dilation rate 不能有大于1的公约数。比如 [2, 4, 6] 则不是一个好的三层卷积，依然会出现 gridding effect。

第二个特性是，我们将 dilation rate 设计成 锯齿状结构，例如 [1, 2, 5, 1, 2, 5] 循环结构。

第三个特性是，我们需要满足一下这个式子：

其中 是 i 层的 dilation rate 而 是指在 i 层的最大dilation rate，那么假设总共有n层的话，默认 。假设我们应用于 kernel 为 k x k 的话，我们的目标则是 ，这样我们至少可以用 dilation rate 1 即 standard convolution 的方式来覆盖掉所有洞。

实际上，在下采样发生后，不是对所有层使用相同的扩张速率，我们对每一层使用不同的扩张速率。在我们的网络中，膨胀率的分配遵循锯齿波式启发式：将多个层组合在一起以形成具有增加的膨胀率的波的“上升沿”，并且下一组重复相同的模式。例如，对于具有膨胀率= 2的所有层，

我们将3个后续层组成一组，并将它们的膨胀率分别改变为1,2和3。通过这样做，顶层可以从与原始配置相同的区域中的更宽范围的像素访问信息（图2（b））。这个过程在所有层中重复，从而使得感知域在顶层不变。

HDC的另一个好处是它可以在整个过程中使用任意的扩张速率，从而自然地扩大了网络的接收区域，而无需添加额外的模块，这对于识别相对较大的对象非常重要。 然而，需要注意的一件重要事情是，组内的膨胀率不应该具有共同的因子关系（如2,4,8等），否则网格问题仍将适用于顶层。

这是我们的HDC方法与atrous空间金字塔池（ASPP）模块或上下文聚合模块之间的关键差异，其中使用了具有通用因子关系的扩张因子。 此外，HDC自然地与网络的原始层集成，而不需要像ASPP或上下文聚合模块那样添加额外的模块。

七、多尺度分割的另类解：Atrous Spatial Pyramid Pooling（ASPP）

在处理多尺度物体分割时，我们通常会有以下几种方式来操作：

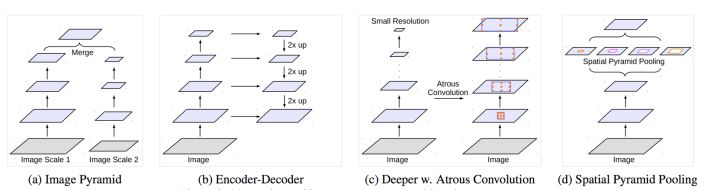
仅仅在一个卷积分支网络下使用 dilated convolution 去抓取多尺度物体是一个不正统的方法。比方说，我们用一个 HDC 的方法来获取一个大（近）车辆的信息，然而对于一个小（远）车辆的信息都不再受用。假设我们再去用小 dilated convolution 的方法重新获取小车辆的信息，则这么做非常的冗余。基于港中文和商汤组的 PSPNet 里的 Pooling module （其网络同样获得当年的SOTA结果），ASPP 则在网络 decoder 上对于不同尺度上用不同大小的 dilation rate 来抓去多尺度信息，每个尺度则为一个独立的分支，在网络最后把他合并起来再接一个卷积层输出预测 label。这样的设计则有效避免了在 encoder 上冗余的信息的获取，直接关注与物体之间之内的相关性。

对于在DeepLabv2中提出的ASPP模块，其在特征顶部映射图并行使用了四种不同采样率的空洞卷积。这表明以不同尺度采样是有效的，我们在DeepLabv3中向ASPP中添加了BN层。

不同采样率的空洞卷积可以有效的捕获多尺度信息，但是，我们发现随着采样率的增加，滤波器的有效权重(权重有效的应用在特征区域，而不是填充0)逐渐变小。当采用具有不同atrous rates的3×3 filter应用到65×65 feature map时，在rate值接近于feature map 大小的极端情况，该3×3 filter不能捕获整个图像内容嘻嘻，而退化成了一个简单的1×1 filter， 因为只有中心 filter 权重才是有效的。

针对上面的问题，并将全局内容信息整合进模型中，则采用图像级特征。采用全局平均池化(global average pooling)对模型的feature map进行处理，将得到的图像级特征输入到一个1×1 convolution with 256 filters(加入 batch normalization)中，然后将特征进行双线性上采样(bilinearly upsample)到特定的空间维度。
改进了ASPP包含：

即，当output_stride=16时，包括一个1×1 convolution和3×3 convolutions，其中3×3 convolutions的rates=(6,12,18)，(所有的filter个数为256，并加入batch normalization)。需要注意的是，当output_stride=8时，rates将加倍；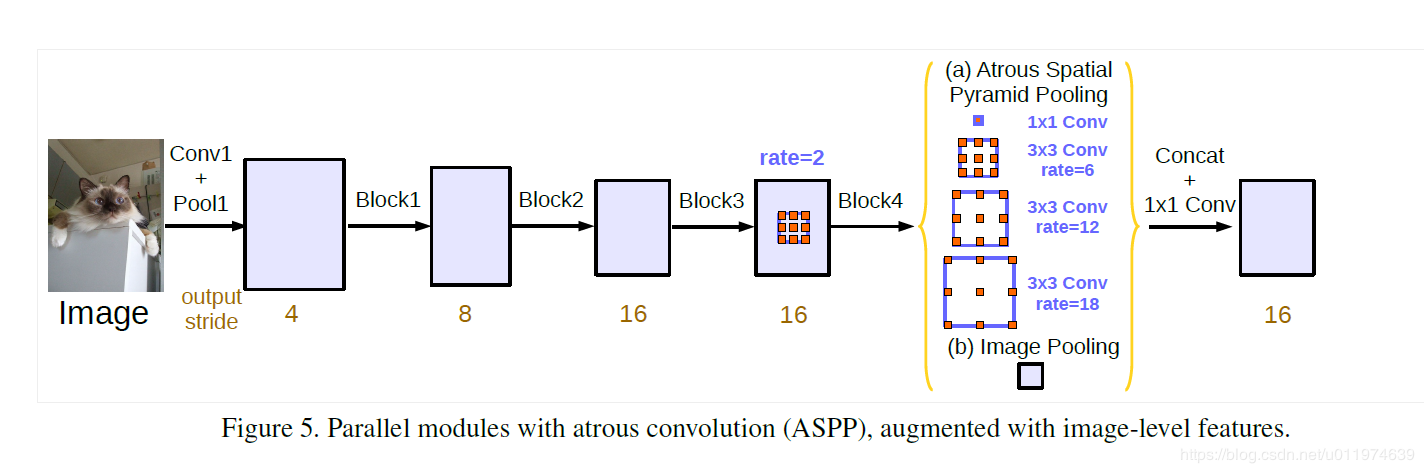

 

参考：https://blog.csdn.net/u011974639/article/details/79144773
https://blog.csdn.net/gzq0723/article/details/80153848