分布式入门之5:paxos
paxos是去中心化协议。目的是在没有中心节点统筹的情况下,通过约定的算法推进流程,使所有节点达到一个一致的状态(批准某个值)
proposer, accepter是其中的主要角色。前者发起投票,后者批准投票。
核心思想是,一旦超过半数的accepter同意某个投票,整个流程结束,批准的那个结果则是最终结果。
learner是另一个角色,从各accepter获取到最终的值。实际中,这些角色可能是同一个节点。
不同的proposer去争抢一半以上的accepter,直观上会遇到的问题就是死锁。为了解决这个问题,paxos引入轮次的概念来避免死锁。
引入轮次后,需要确保的隐含条件就是:如果其中一轮已经选举出了一个结果,则后续所有轮次不能再推翻此结果,而必须接受此结果。
协议流程如下:
paxos过程与两阶段提交类似,也分两个阶段。
第一阶段是proposer告诉acceptor,准备提交第n轮,需要保证不接受小于n轮的其他proposer的提案。
第二阶段,则是根据第一阶段acceptor的返回结果,通知acceptor提交某个值。
理解算法需要重点关注下面的思想:
- 各个proposer之间是一种“互助”角色,而不是“互斥”。一个轮次的prepared消息,会“帮助”整个系统把当前最有希望成为最终值的value提交上去。只有在别人都没有提交过的情况下,才会提交自己的值 。是一个害羞性算法。
- 各个acceptor上,存储了两个信息,即(已知轮次、已批准值)这一对数据。对应与下图的n与V。下图V_N的意思,则是在第N轮已经批准过一个V值。
流程如下:
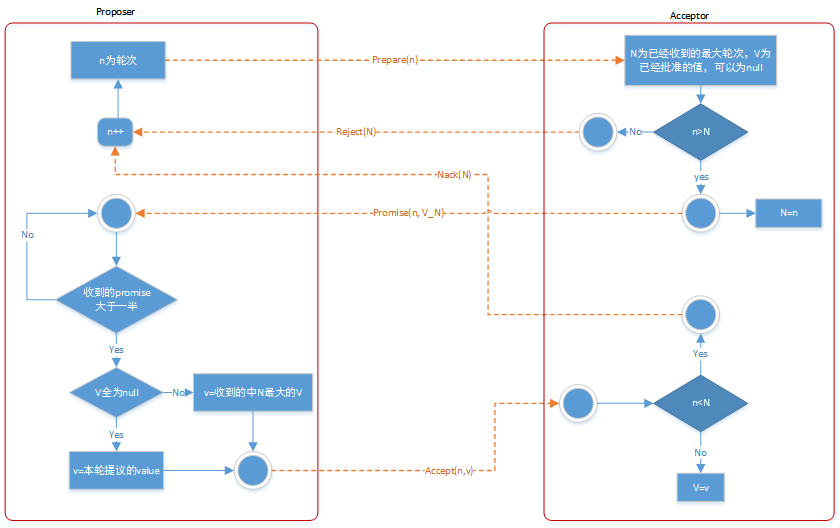
要点为:
只有prepare后收到的“大多数”全为空时,才能进行提案新的v;否则,只能在收到的大多数中,选择一个轮次最高被批准的。
如果试图在第二阶段提案某个低轮次的值,会被直接Nack打回。注意,只要有reject与nack,不论是否多数,提交者本轮立即失败。
如何保证已经在X轮批准了V1后,后续的轮次不再批准其他值?
符合以上问题的场景有两种:
- 第一种是新提一个值推翻旧值,这是不可能的:
X轮批准了V1后,说明X轮中已经有“大多数”acceptor已经记下了V1。而要想再批准其他值,需要在prepare后收到的“大多数”中全为空,这是不可能的,至少会有一个V1。这论证了是不可能提出新值的。
- 第二种场景是,X轮批准了V1后,只是代表其中有“大多数”中的轮次最高为V1。会不会存在着已被少数派批准的另一个值V2在后续轮次中翻盘,后续轮次将多数派的V1覆盖掉(即V2轮次高于已批准的v1)?
可惜也是不可能的。高轮次少数派V2如果存在,有两种可能:
a. 是在V1得到批准前批准的。那么当V1在第二阶段的提交accept的过程中,会发现有高轮次的值V2已经批准,从而再也不可能取到多数派的通过。(accept中,轮次比较旧的提交直接会被acceptor以Nack打回)。被打回后,老实使用新的轮次来prepare,这时会取到多数派的V2并在后续的accept消息中代为提交。
b. 少数派的V2值是在V1被选举出来后才出现的。这显然不可能,第一种想像场景中已经讨论过了,不可能有新值被提交上来了。
轮次n:
可见,轮次是个全局的概念,如何保证轮次在整个过程中不同节点轮次不重叠。
只需要定一个保证递增性与唯一性的规则。如:
时间戳 + 提出提案的次数 + 机器 IP/机器ID。活锁:
虽然paxos以轮次概念的引入解决了死锁,但因为存在着prepare、accept两阶段,有可能出现活锁问题:
如proposer A以prepare 1发起一轮paxos过程,所有acceptor返回null,A准备发送accept(1, Va);
此时proposer B以prepare 2发起又一轮paxos,所有acceptor依然返回null,B准备发送accept(2, Vb);
这时,proposer A以prepare 3继续发起新一轮prepare。。。,循环往复。这就是活锁。
活锁可使用随机改变轮次n的增长幅度来解决;或者是指定一个主的proposer,让其来提案。



