学习js 优先级

以前很少关注js优先级 主要哦是技术菜鸟老加班没时间技术菜鸟

最重要的是记不住特点。。。。。。。。。。

1级

. [] ()

字段访问、数组索引、函数调用和表达式分组

通过观察可以发现

. 字段访问--》读取数据

[] 数组索引--》读取数据                ps [] 这个也可以创建空数组 不知道为啥没有算进去

() 括号 分为函数调用--》读取作用域

               表达式分组

二级

++ -- - ~ ! delete new typeof void

一元运算符、返回数据类型、对象创建、未定义的值

 

 

所有一元运算符，如 ~ 运算符，以如下规则来求表达式的值：

• 如果将它用于 undefined 或 null 表达式，则产生一个运行时错误。
• 对象被转换成字符串。
• 如果可能，字符串被转换为数字。如果不能，则产生一个运行时错误。
• Boolean 值被当作数字（如果是 false 则为 0，如果是 true 则为 1）。

用该运算符来生成数字。

~ 运算符查看表达式的二进制表示法的值，并执行按位非操作。该操作的结果如下所示：

0101   (expression)
----
1010   (result)

表达式中的任何一位为 1，则在结果中相应位变为 0。表达式中的任何一位为 0，则在结果中相应位变为 1。

二级优先级里面 大部分是一元操作符 和后缀表达式外加一个new

第三极

* / %

相乘、相除、求余数

第三级 就简单了 乘除求余 元算

第四级别

+ - +

相加、相减、字符串串联

这里加法和减法 我理解 不知道为啥把字符串串联也单独拉出来。。。。。

加法作用于数字

+运算符作用于两个数字类型的操作数时表示加法，产生两个操作数之和。-运算符表示剑法，产生两个数字之差。

加法是满足交换律的运算，但是不总满足结合律。

加法遵循IEEE 754二进制双精度幅度浮点算法规则：

• 两个正负号相反的无穷之和为NaN。
• 两个正负号相同的无穷大之和是具有相同正负的无穷大。
• 无穷大和有穷值之和等于操作数中的无穷大。
• 两个负零之和为-0。
• 两个正零，或者两个正负号相反的零之和为+0。
• 零与非零有穷值之和等于非零的那个操作数。
• 两个大小相等，符号相反的非零有穷值之和为+0。
• 其它情况下，既没有无穷大也没有NaN或者零参与运算，并且操作数要么大小不等，要么符号相同，结果计算出来后会按照IEEE 754 round-to-nearest模式取到最接近的能表示的数。如果值过大不能表示，则结果为相应的正负无穷大。如果值过小不能表示，则结果为相应的正负零。ECMAScript要求支持IEEE 754规定的渐进下溢。

-运算符作用于两个数字类型时表示减法，产生两个操作数之差。左边操作数是被减数右边是减数。给定操作数a和b，总是有a–b产生与a + ( -b )产生相同结果。

第五级别

<< >> >>>

移位

左移一位相当于该数乘以2，左移2位相当于该数乘以2^2=4。上面举的例子15<< 2=60，即乘了4。但此结论只适用于该数左移时被溢出舍弃的高位中不包含1的情况。

15<< 2=60，即乘了4

8 << 1的值为8*2=16；

8 << 2的值为8*(2^2)=32；

8 << n的值为8*（2^n）。

>>(带符号右移)

右移一位相当于除2，右移n位相当于除以2的n次方。这里是取商哈，余数就不要了。

>>>(无符号右移)

第六级别

< <= > >= instanceof

小于、小于或等于、大于、大于或等于、是否为特定类的实例

第七级别

== != === !==

相等、不相等、全等，不全等

严格等于比较算法

比较 x===y，x 和 y 为值，需要产出 true 或 false。比较过程如下：

1. 如果 Type(x) 与 Type(y) 的结果不一致，返回 false，否则
2. 如果 Type(x) 结果为 Undefined，返回 true
3. 如果 Type(x) 结果为 Null，返回 true
4. 如果 Type(x) 结果为 Number，则
   1. 如果 x 为 NaN，返回 false
   2. 如果 y 为 NaN，返回 false
   3. 如果 x 与 y 为同一个数字，返回 true
   4. 如果 x 为 +0，y 为 -0，返回 true
   5. 如果 x 为 -0，y 为 +0，返回 true
   6. 返回 false
5. 如果 Type(x) 结果为 String，如果 x 与 y 为完全相同的字符序列（相同的长度和相同的字符对应相同的位置），返回 true，否则，返回 false
6. 如果 Type(x) 结果为 Boolean，如果 x 与 y 都为 true 或 false，则返回 true，否则，返回 false
7. 如果 x 和 y 引用到同一个 Object 对象，返回 true，否则，返回 false

此算法与 SameValue 算法在对待有符号的零和 NaN 上表现不同。

还有 几个级别

C++用 ^ 运算符实现按位异或运算   
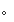
expression1^expression2   
参与运算两值两相应bit位相同则结0否则1   即：   
0^0 = 0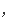   
1^0 = 1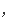   
0^1 = 1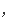   
1^1 = 0