拉格朗日乘子法
对于含有等式约束的优化问题: \( \underset{x}{\operatorname{\mathop{\min}}} f(x)\ \ {\operatorname{s.t.}}\ h_i(x)=0, i = 1,2,...,m \),在等式 \( h_i(x) = 0 \) 非常复杂而难以带入目标函数 \( f(x) \) 的时候,拉格朗日乘子法可以免去这个变量替换过程。
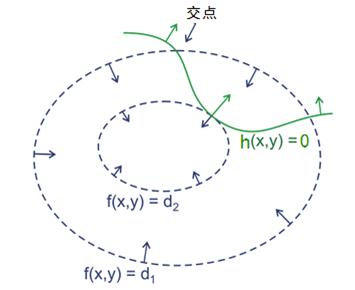
1. 如果目标函数在不含约束条件下的极值点满足约束条件,则约束条件形同虚设;否则,其最优点位于目标函数 \( f(x) \) 的等高线和条件方程 \( h_i(x)=0 \) 的切点处。因为,目标函数 \( f(x) \) 的等高线与条件方程 \( h_i(x)=0 \),只能相切或者相交。在交点上,目标函数可以沿着条件方程变大,也可以沿着条件方程变小;但是,在切点处,目标函数沿着条件方程,只能有一个变化方向。所以,最优点必定在目标函数 \( f(x) \) 的等高线和条件方程 \( h_i(x)=0 \) 的切点处。
2. 目标函数 \( f(x) \) 的等高线与条件方程 \( h_i(x)=0 \) 相切,又等价于目标函数 \( f(x) \) 与条件方程 \( h_i(x)=0 \) 所构成的函数 \( h_i(x) \) 梯度平行,等价于拉格朗日算子 \( L(x, \alpha) = f(x) + \sum_{i=1}^{m} \alpha_i h_i(x) \) 对 $ x $ 的导数等于零:\( \nabla_x L(x, \alpha) = \nabla_x f(x) + \sum_{i=1}^{m} \alpha_i \nabla_x h_i(x) = 0 \),这就是取到最优点需要的条件;而 $ L(x, \alpha) $ 对拉格朗日乘子 $ \alpha $ 的导数等于零:\( \nabla_\alpha L(x, \alpha) = 0 \),等价于等式约束条件。
KKT 条件
对于含有不等式约束的优化问题 \( \underset{x}{\operatorname{\mathop{\min}}} f(x)\ \ {\operatorname{s.t.}}\ h_i(x)=0,\ g_j(x) \le 0,\ i = 1,2,...,m,\ j=1,2,...,n \),其拉格朗日算子在形式上同含有等式约束的优化问题类似:\( L(x, \alpha, \beta) = f(x) + \sum_{i=1}^{m} \alpha_i h_i(x) + \sum_{i=j}^{n} \beta_j g_j(x) \) 。因为等式约束 $ h_i(x)=0 $ 等价于 \( h_i(x) \le 0\ and -h_i(x) \le 0 \),因此,可以只考虑不等式约束 $ g_j(x) \le 0 $。
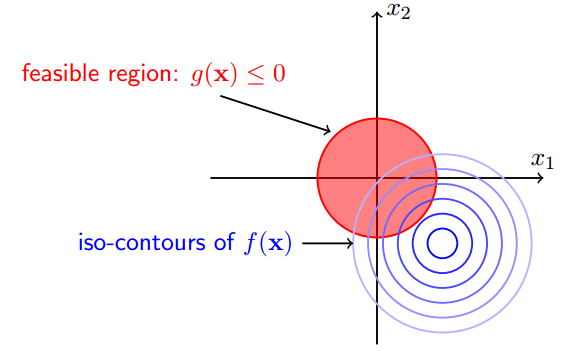
A. 不等式约束 \( g_j(x) \le 0 \) 是一个空间区域,同样地,目标函数 \( f(x) \) 在没有约束条件下的极值点,要么在该空间区域内,要么不在。1. 当在这个空间里的时候,令其拉格朗日乘子 $ \beta_j $ 为零,使得拉格朗日算子等同于目标函数 \( f(x) \) 即可。2. 当目标函数 \( f(x) \) 在无约束条件下的极值点,不在这个不等式约束空间 \( g_j(x) \le 0 \) 里的时候,含有不等式约束条件 \( g_j(x) \le 0 \) 的优化问题的极值点,就只能尽最大可能靠近无约束条件的优化问题的极值点。在限制了求的是目标函数 \( f(x) \) 的极小值,即要到达最靠近目标函数 “谷底” 的地方,以及不等式约束 \( g_j(x) \le 0 \) 是某个函数值 \( g_j(x) \) 小于等于零之后,可以设想不等式约束 \( g_j(x) \le 0 \) 所构成的函数 \( g_j(x) \) 的等高线,它和目标函数 \( f(x) \) 的等高线交叠,两个 “山谷” 的边界就是不等式约束 \( g_j(x) \le 0 \) 取等号的方程,即 \( g_j(x) = 0 \) 的位置。当沿着不等式约束 \( g_j(x) \le 0 \) 所构成的函数 \( g_j(x) \) 的负梯度方向 “走” 的时候,即靠近不等式约束所围成的空间区域的中心,而远离不等式取等号所在的边界时,目标函数 \( f(x) \) 却是在 “上坡”,因此,含不等式约束 \( g_j(x) \le 0 \) 的目标函数 \( f(x) \) 的极小值点就在不等式取等号的地方,即 \( g_j(x) = 0 \),这是最靠近目标函数 “谷底” 的位置。因此,不管目标函数 \( f(x) \) 在无约束条件下的极值点是否满足 \( g_j(x) \le 0 \),都有 \( \beta_j g_j(x) = 0 \)。
B. 以及,因为限制了求的是目标函数 \( f(x) \) 的极小值,以及不等式约束是某个函数值 \( g_j(x) \) 小于等于零,所以,目标函数 \( f(x) \) 和不等式约束 \( g_j(x) \le 0 \) 所构成的函数 \( g_j(x) \)是两个 ”山谷“,因此,在不等式条件去等号的位置上,两个 “山谷” 的梯度方向不只是平行,更是反向的,这又对应于使拉格朗日算子 \( L(x, \alpha, \beta) \) 对变量 $ x $ 的导数取零,即 \( \nabla_x L(x, \beta) = \nabla_x f(x) + \sum_{i=1}^{m} \beta_j\nabla_x g_j(x) = 0 \) 需要满足的条件:\( \beta_j \ge 0 \)。因而,在 \( \beta_j g_j(x) = 0 \) 中有 $ \beta_j \ge 0 $ 以及 $ g_i(x) \le 0 $,称为松弛互补条件。综上所述,拉格朗日乘子法推广到不等式约束,需要满足 KKT 条件,一共有 5 个:
\( \nabla_x L(x, \alpha, \beta) = 0 \quad h_i(x)= 0 \quad g_j(x) \le 0 \quad \beta_j g_j(x) = 0 \quad \beta_j \ge 0,\ i=1,2,...,m\ j=1,2,...,n \)
对偶问题
前面,通过几何的视角,分析和证明了拉格朗日乘子法在 KKT 条件下,等价于原始优化问题。接下来,将通过解析的方法,分析拉格朗日乘子法所构成的原问题及其对偶问题的关系。对于原来的优化问题 \( \underset{x}{\operatorname{\mathop{\min}}} f(x)\ {\operatorname{s.t.}}\ h_i(x)=0,\ g_j(x) \le 0,\ i = 1,2,...,m,\ j=1,2,...,n \),其拉格朗日乘子法形式为:\( L(x, \alpha, \beta) = f(x) + \sum_{i=1}^{m} \alpha_i h_i(x) + \sum_{i=j}^{n} \beta_j g_j(x),\ i = 1,2,...,m,\ j=1,2,...,n \)。
A. \( \theta_P(x) \overset{let}{=} \underset{\alpha, \beta: \beta \ge 0}{\mathop{\max}} L(x, \alpha, \beta)\ \Rightarrow\ \underset{x}{\mathop{\min}} \theta_P(x) = \underset{x}{\mathop{\min}} \underset{\alpha, \beta: \beta \ge 0}{\mathop{\max}}\ L(x, \alpha, \beta)\ = \underset{x: h(x)=0,\ g(x) \le 0}{\operatorname{\mathop{\min}}} f(x) \)
\( \because\ \begin{equation} \begin{cases} \underset{\alpha, \beta: \beta \ge 0}{\mathop{\max}} L(x, \alpha, \beta) = \infty,\ if\ \exists\ g_j(x)>0\ or\ h_i(x) \ne 0; \\ \underset{\alpha, \beta: \beta \ge 0}{\mathop{\max}} L(x, \alpha, \beta) = f(x),\ else.\\ \end{cases} \end{equation} \)
\( \therefore\ \underset{x}{\mathop{\min}} \underset{\alpha, \beta: \beta \ge 0}{\mathop{\max}} L(x, \alpha, \beta) = \underset{x}{\mathop{\min}} \{ \infty, f(x) \} = \underset{x: h(x)=0,\ g(x) \le 0}{\operatorname{\mathop{\min}}} f(x) \)
可见,该形式可以将关于 $ x $ 的约束条件 \( h(x)=0,\ g(x) \le 0 \) “吸收” 到 $ \theta_P(x) $ 中;以上,称为原问题的无约束形式,其最优值为 \( p^* = \min_x \theta_P(x) = \theta_P(x^*) \)。
B. 对偶问题为:\( \underset{\alpha, \beta: \beta_j \ge 0}{\mathop{\max}} \underset{x}{\mathop{\min}} L(x, \alpha, \beta) \)。\( \theta_D(\alpha, \beta) \overset{let}{=} \min_x L(x, \alpha, \beta) \),其最优值为 \( d^* = \underset{\alpha, \beta: \beta_j \ge 0}{\mathop{\max}} \theta_D(\alpha, \beta) = \theta_D(\alpha^*, \beta^*) \)。因为 \( \max_x \min_y f(x, y) \le \min_y \max_x f(x) \),所以,\( d^* \le p^* \),称为 “弱对偶关系”,玩笑话来说就是,鸡头再好也比不过凤尾。但是,当问题是凸优化问题,等式约束 $ h(x) $ 为放射变换,不等式约束满足 Slater 条件,即 \( \exists\ g_i(x) = 0 \) 时,有 \( d^* = p^* \),称为 “强对偶关系”,证明略。并且,由 “弱对偶” 变成 “强对偶”,也就是 $ \le $ 变成 $ = $ 以后,同样可以推出松弛互补等 KKT 条件;但是,反之不成立,也就是说 Slater 条件等是强对偶条件的充分条件,KKT 条件为强对偶条件的必要条件。
参考:
含等式约束:拉格朗日乘子法
含不等式约束:KKT 条件
拉格朗日乘子法:对偶问题
shuhuai007-机器学习-白板推导系列-支持向量机


 浙公网安备 33010602011771号
浙公网安备 33010602011771号