dp:最大子矩阵面积
在一个平面内随机出现一些连续的区域,以这些区域构成一个矩形,求最大的矩形面积。
解决这一类问题的思路是:枚举所有高度,通过记忆化记录左右侧最远能到达的区域。
以下以一个类似柱状图的模型来说明:
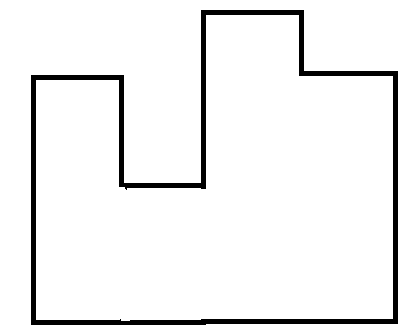
要求求出图中最大的矩形面积。
图中存在四个不同的高度。
高度1左右都没有更高的,记l1=1,r1=1
高度2是最低的,记l2=1,r2=4
高度3左右都没有更高的,记l3=1,r3=4
高度4左侧有一个更高的,记l4=3,r4=4
由于更高有继承性(如已知a比b高,当b比c高时,c可以直接跳到a处)
该记忆化可以用以下代码实现:
a[0]=-1;//高度 a[n+1]=-1; FOR(j,1,n) l[j]=j,r[j]=j;//左右能到达 l[0]=1; r[n+1]=n; FOR(j,1,n) while(a[l[j]-1]>=a[j]) l[j]=l[l[j]-1]; ROF(j,n,1) while(a[r[j]+1]>=a[j]) r[j]=r[r[j]+1];
要注意l和r的遍历方向是不同的。
复杂度为O(n)。



