ACM-ICPC 2018 南京赛区网络预赛 B，J

B. The writing on the wall

 

观察数据范围，n*m的矩阵(n<=1e5,m<=1e2）

m的范围这么小，我们显然可以构造一个复杂度为O(n*m*m)的算法，那么这是否可行呢？

显然我们可以用n*m的时间遍历每一个矩阵，再用m的时间找出以这个矩阵为右下角顶点（假设我们遍历顺序为从左到右，从上到下）的任意规格矩阵。

那么难点便在于如何找出以其为右下角顶点的矩阵：

 

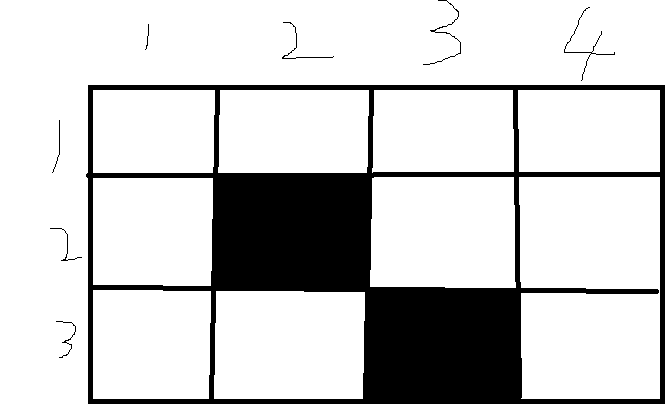
令当前情况如图，我们现在处于第四列第一行

此刻，（4，1）左侧包括自己一共有4个矩阵，而我们能数出来的矩阵数目为四：1*1，2*1，3*1，4*1 ，它们的共同特点是：宽度都为1

在(4，2)左侧包括自己一共有2个矩阵，而我们能数出来的矩阵数目为二：1*2，2*2，它们的共同特点是：宽度都为2

在（4，3）左侧包括自己一共有1个矩阵，而我们能数出来的矩阵数目为一：1*3，它们的共同特点是：宽度都为3

为了防止误解，再加一份示例：

 

在（4，1）左侧包括自己一共有1个矩阵，而我们能数出来的矩阵数目为一：1*1，它们的共同特点是：宽度都为1

在（4，2）左侧包括自己一共有1个矩阵，而我们能数出来的矩阵数目为一：2*2，它们的共同特点是：宽度都为2

在（4，3）左侧包括自己一共有1个矩阵，而我们能数出来的矩阵数目为一：1*3，它们的共同特点是：宽度都为3

 

也就是说主要思路是三个for循环，前两个遍历矩阵，最后一个遍历为：以该矩阵为右下角，能构造的矩阵的宽度。

 

 

 

J. Sum

 

用素数筛打表构造题目要求的函数，然后求前缀和

打表函数如下：

ll prim[MAXN],ans[MAXN],cnt,k,l;
bool vis[MAXN];
void init()
{
	mst(vis);
	cnt=0;
	ans[1]=1;
	for(int i=2;i<=2e7;i++)
	{
		if(vis[i]==0) prim[++cnt]=i,ans[i]=2;
		for(int j=1;j<=cnt;j++)
		{
			k=prim[j]*i;
			vis[k]=1;
			if(i%prim[j]) ans[k]=ans[i]*ans[prim[j]];/*不含平方因子 */
			else
			{
				l=prim[j]*prim[j];
				if(i%l==0) ans[k]=0;/*含立方因子 */
				else ans[k]=ans[k/l];/*含平方因子 */
			} 
		}
	}
}