特殊数及其用法

卡特兰数：

有两个维度，限制一个维度（长度为n）不得超过另一个维度（长度为m），所存在的合法方案数为卡特兰数：( C(m+n,n) - C(m+n,m+1) ) * m! * n!或( C(m+n,n) - C(m+n,n-1) ) * m! * n!

n==m时表示为（2n)!/(n!*n!)*(1/(n+1))

扩展：有k个维度，每个维度长度为n，且维度之间依次存在限制

方案数为

2！*3!....*(k-1)!*(k*n)!/(n!*(n+1)!*......(n+k-1)!)

 

斯特林数：

第一类：将n个元素分为m个圆排列的方案数

s(n,m)的递推公式： s(n,m)=(n-1)*s(n-1,m)+s(n-1,m-1) ,1<=k<=p-1

边界条件：s(p,0)=0 ,p>=1  s(p,p)=1  ,p>=0

第二类：将n个元素分为m个集合的方案数

构造方法见贝尔数

 

贝尔数：

 集合中有n个元素，将该集合进行划分，划分的方案数为贝尔数。没有一般表达式

构造方法：

1.每行第一个元素等于上一行最后一个元素

2.此外每个元素等于其左侧和左上元素之和

一个三角形阵：

1

1 2

2 3 5

5 7 10 15

每行第一个为贝尔数，每行之和为第二类斯特林数。

此外贝尔数存在以下性质：

1.(Bp+n)=(Bn)+(Bn+1)%p(p为素数)

2.(Bp^m+n)=m(Bn)+(Bn+1)%p(p为素数)

由2可以求出模p时，贝尔数的周期为(p^p-1)/(p-1)

 

斯特灵公式：

求n!，值为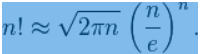

可以通过ln（）求出n！的位数