数论:从辗转相除法到逆元
辗转相除法:
int gcd(int x,int y)
{
return y>0?gcd(y,x%y):x;
}
相信大部分人都比较熟悉了,简单又快速的求最大公约数的利器,甚至不需要知道原理也不影响使用。
现在讲解一下原理及其证明:
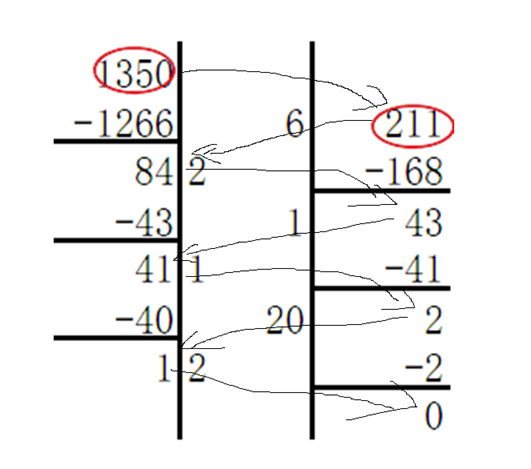
这张图的运算流程如下:
1350%211=84
211%84=43
84%43=41
43%41=2
43%2=1
2%1=0
故1为1350,211的最大公约数
然后,如何证明gcd是对的呢?
首先有两个正整数x,y,我们令x>y;
令z=gcd(x,y);
在这个条件下,x%z==0,y%z==0;
所以对于任何合法的n,m
都存在(mx+ny)%z==0(合法指使mx+ny>0) 等式1:(mx+ny)%z==0
我们再令x=ky+b (k=x/y,b=x%y)
变形成x-ky=b (将ky移到左边) 等式2:x-ky=b(k=x/y,b=x%y)
我们可以发现在等式1中
如果令m=1,n=-k,则会变成等式2,且这个值是合法的。
因此(x-ky)%z==b%z==0;(k=x/y,b=x%y)
现在整理一下结论:
1. z是x,y的gcd
2. b=x%y
3. b%z=0
所以z同时是x,y,x%y的约数(但未证明是最大的)
距离结论我们还需要证明:z是y,x%y的最大公约数
反证法:
令x=Xz,y=Yz,带入等式2:x-ky==b (b=x%y)
以下我们假设存在g(g>1),使y与x%y的最大公约数为zg。
x%y==(X-kY)z;
令X-kY=cg,Y=dg (g>1),则X==kY+cg==kdg+cg==(kd+c)g,则x==Xz==(kY+c)zg,y==Yz==dzg,故x与y最大公约数成为zg,而非z,矛盾
得证。
顺带一提,辗转相除法的复杂度是log2(max(x,y))
贝祖等式:
c=gcd(a,b)
当d为c的倍数时
ax+by=d恒有整数解
所有解中,有且仅有一个解(x,y)满足且-b<=x<=b,-a<=y<=a
扩展欧几里得算法:
在求c=gcd(a,b)时,同时求出贝祖等式:ax+by=c的一个整数解(所以扩欧有五个参数)
原理演示:
求18x+5y=1的解
18%5=3,18=5*3+3,3=18+5*(-3)
5%3=2,5=3*1+2,2=5+3*(-1)
3%2=1,3=2*1+1,1=3+2*(-1)
然后从下向上进行处理
1=3+2*(-1)
1=3+(5+3*(-1))*(-1) (第二个式子代入)
=3*2+5*(-1)
0=(18+5*(-3))*2+5*(-1)(第一个式子代入)
=18*2+5*(-7)
则(2,-7)为一个解
建议自己选几个数据算一算
ll exgcd(ll a,ll b,ll& d,ll& x,ll& y)
{
if(!b){d=a,x=1,y=0;}
else
{
exgcd(b,a%b,d,y,x);
y-=x*(a/b);
}
}
再看代码就很好理解了
取模,逆元与扩欧:
个人觉得求逆元的最好算法就是扩欧,效率极高。
介绍一下逆元是什么
在取模的条件下(如:所有数字都对mod取模)
有c=(a*b)%mod
令inv(b,mod)为b的逆元
则(c*inv(b,mod))%mod=a
也就是乘一个数的逆元相当于“除这个数”
那我们为什么不能直接除呢?因为在取模中使用除法是非常麻烦的.
给出一个简单的例子:
a=3,b=?
c=2=(a*b)%4
如果我们试图用除法求b的值会怎样?
事实上b=2,这是用除法难以算出来的。
取模计算对于加减乘都有结合律,分配律,唯独除法是不成立的。
取模运算的证明:
令a=ki+x,b=kj+y,模为k
(a+b)%k=((i+j)*k+x+y)%k=(x+y)%k
(a%k+b%k)%k=(x+y)%k
(a*b)%k=(k*k*i*j+k*(jx+iy)+xy)%k=xy%k
((a%k)*(b%k))%K=(x%k*y%k)%k=xy%k
(a/k)%k=x%k
(a%k)/k=x/k不相等
总结规律如下:
(a+b)%p=(a%p+b%p)%p(1)
(a-b)%p=(a%p-b%p)%p(2)
(a*b)%p=(a%p*b%p)%p(3)
a^b%p=((a%p)^b)%p(4)
结合律:
((a+b)%p+c)%p=(a+(b+c)%p)%p(5)
((a*b)%p*c)%p=(a*(b*c)%p)%p(6)
交换律:
(a+b)%p=(b+a)%p(7)
(a*b)%p=(b*a)%p(8)
分配律:
(a+b)%p=(a%p+b%p)%p(9)
((a+b)%p*c)%p=((a*c)%p+(b*c)%p)%p(10)
然后,让我们思考,扩欧与逆元是如何结合在一起的。
假如模为b,求a的逆元
用扩欧有:
ax+by=gcd(a,b)
这里补充一个知识,大部分题目取模的模数都是素数,如998244353,1e9+7
所以几乎所有情况下都保证a,b互质
所以gcd(a,b)=1
对式子两边求模b
ax%b+by%b=1%b
ax%b=1%b
假如我们要对一个数“除a”,不妨设这个数为ak,对于任意的k
都存在((ak)%b*x)%mod=((ax)%b*k)%b=1*k%b
所以x就是a的逆元
void exgcd(ll a,ll b,ll& d,ll& x,ll& y)
{
if(!b){d=a;x=1;y=0;}
else
{
exgcd(b,a%b,d,y,x);
y-=x*(a/b);
}
}
ll inv(ll a,ll n)
{
ll d,x,y;
exgcd(a,n,d,x,y);
return (x+n)%n;
}
另外,我们可以看到返回的数字并不是x,而是(x+n)%n,这个涉及到取模的定义
首先,取模意味着,返回结果必须是正数
而通过exgcd得出的x是正负不明的
所以在任何涉及取模的运算中,要将可能为负的数变成正数



