树形dp粗解
树的性质:n个点,n-1条边,任意两个点之间只存在一条路径,可以人为设置根节点,对于任意一个节点只存在至多一个父节点,其余为子节点。
记忆化树形dp模型较为抽象难以理解,以下通过由浅到深的方式解析树形dp以及树的性质。
树形dp求树的直径:(在一颗树里找到点X,Y,使得|XY|最大)
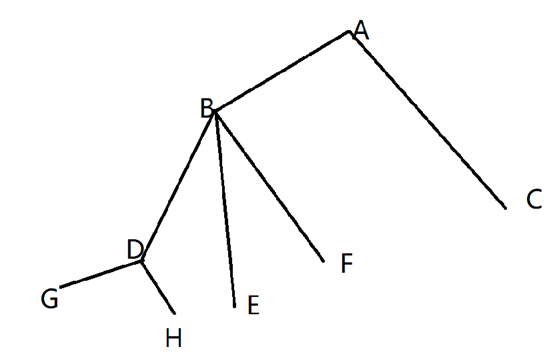
如图,我们令A为根节点,令dfs遍历顺序为ABDGHEFC。
在我们的dfs计算中,我们从下往上对每一个节点,找到其最长的两个子树路径(两个没有重复路径的子树,例如节点B为BDG+BF,而不会出现BDG+BDH),并更新答案(ans=BDG+BF),然后将其中最长的子树路径上传给父节点(对于点A,B上传的只有最长的BDG),在A节点,得知最长的两个子树路径(ABDG+AC),并更新答案(ans=ABDG+AC)
处理方式如下:
根据思路,代码分为两个处理部分:更新答案和更新当前节点最长子树路径,其中更新答案是读取当前访问的子树中最长的子树路径(记为dp【子】),将其与现在该节点记录的最长子树(记为dp【当前】)相连来查看答案是否能更新,然后,如果dp【子】比dp【当前】大,则更新dp【当前】为dp【子】。
代码如下:
struct num
{
int nex,val;
};
void dfs(int u,int fa)
{
for(int i=0;i<q[u].size();i++)
{
int v=q[u][i].nex;//子节点
if(v!=fa)
{
dfs(v,u);//先遍历
ans=max(ans,dp[u]+dp[v]+q[u][i].val);//更新答案
dp[u]=max(dp[u],dp[v]+q[u][i].val);//更新节点
}
}
}
留下思考点:(底部有解析)
1.为何更新答案要早于更新节点
2.dp【节点】的值是什么意思
3.替换根节点会产生影响吗
理解了树形dp的基本结构后,来看一道稍微复杂的题目
Hdu4616:http://acm.hdu.edu.cn/showproblem.php?pid=4616
题意简述:
在一颗有n(n<5e4)个节点的树中,每个节点有权值和是否有陷阱,你可以最多踏进c(c<=3)个陷阱,当你进入第c个陷阱时,你就无法继续移动了,你可以在任意节点出发,获取经过节点的权值(无法重复获取同一个节点),求能得到的最大权值和。
题目和树的直径很相似,实际上获取点的权值和获取边的权值是没有本质区别的。
不过题目中的陷阱是一个比较有意思的元素,我们可以给dp数组增加一个维度(如dp[a][b],表示与节点a相连的子树中,经过b个陷阱时能获得的最大权值和)
但是,这会衍生出一个问题,如下:

假设图中BC点有陷阱,AD点无陷阱,我们最多经过2个陷阱,令A为根节点,那么在C节点时,dp[c][1]=CD,dp[c][0]=0 x在B节点时,dp[b][2]=BCD,dp[b][1]=B,注意dp[b][2]是不会再往A节点衍生的,因为达到了最大陷阱数,所以在A节点时,dp[a][2]=0,dp[a][1]=AB(对于dp表示的值有疑惑的回到上面再思考),此刻我们漏掉了一种情况,即ABC的值。
这个问题可以总结为:当我们访问了最大数量的陷阱时,路径至少要有一个起/终点在陷阱上,而我们的状态不足以得知是否有一个起/终点在陷阱上.
因此,我们需要再增加一维状态表示起点(子树中深度最深的节点)是否在陷阱上
代码如下:
void dfs(int u,int fa)
{
dp[u][go[u]][go[u]]=val[u];//go为1表示有陷阱,val表示权值
for(int i=0;i<q[u].size();i++)
{
int v=q[u][i];
if(v!=fa)
{
dfs(v,u);
FOR(j,0,c)//更新答案
{
FOR(k,0,c-j)
{
ans=max(ans,dp[u][j][1]+dp[v][k][1]);
if(j<c) ans=max(ans,dp[u][j][0]+dp[v][k][1]);
if(k<c) ans=max(ans,dp[u][j][1]+dp[v][k][0]);
if(k+j<c) ans=max(ans,dp[u][j][0]+dp[v][k][0]);
}
}
FOR(j,0,c)//更新节点
{
if(j<c) dp[u][j+go[u]][0]=max(dp[u][j+go[u]][0],dp[v][j][0]+val[u]);
dp[u][j+go[u]][1]=max(dp[u][j+go[u]][1],dp[v][j][1]+val[u]);
}
}
}
}
值得一提的是初始化,dp数组初始化为不够小的值会导致答案错误,数组需要初始为极小值,关于这个情况,discuss中有hack样例。
Bzoj1509:https://www.lydsy.com/JudgeOnline/problem.php?id=1509
逃课的小孩(思路来源于陈瑜希论文)
题意简述:
在一个有n(n<=2e5)个节点的树中,找到三个点XYZ,使得XY<=XZ,求出XY+YZ的最大值。
如果把Y当作确定的点,那么这个命题等价于找出离Y最远的两个点(树的直径为找出最远的两个点),这就类似于求树的直径,复杂度为O(n),然而我们无法直接得知Y点,所以复杂度为O(n*n),在复杂度上无法满足。
或许这里有一个疑问,为什么一定要知道Y点才可以得出答案,难道不能像求树的直径一样吗?看如下情况

令A为根节点,图中直线距离均为1,那么离A最远的点为C和D,距离为2和3,然而2+3不是答案,行动轨迹并不是想当然的C->A->D,因为D更近,所以是C->D->A,答案为1+3,很显然,共享部分路径的最远点的情况较为复杂,并不能通过简单的最远距离存储答案,最开始的简单模型无法应对这么复杂的情况。
枚举分叉点:对于任意的XYZ,必然存在一个分叉点A(可以与Y重合),使得XA,YA,ZA不包含除A以外的交点(树的性质,Y到X和Y到 Z的路径唯一,所以存在唯一的交点A)。枚举分叉点是可以规避上述的复杂情况(因为每条路径不存在重复点),但这又引入了一个问题,即“父节点响应”,接下来解释为什么需要“父节点响应”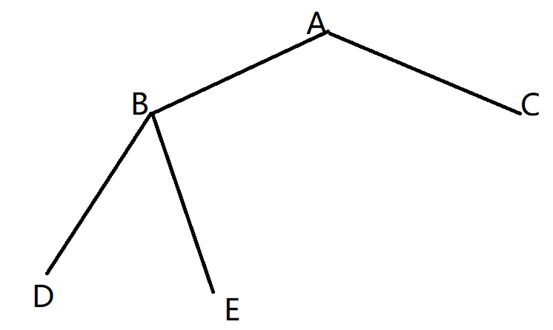
令A为根节点,dfs序为ABDEC,令BD<BE=AB=AC,很显然答案为DB+BE*2+BAC(D->B->E->B->A->C),那么在B节点时,B的信息只有DB和EB(从下往上),上传到A节点的信息只有EBA(枚举分叉点自然不能出现重复边,所以只能上传最大边),A的信息只有EBA和CA,仅靠这些信息时无法得出答案的。除非我们在B节点时能读取到父节点A的信息CA,并与AB相连,不过很显然,我们得到A节点的信息是晚于B节点的,所以我们需要再次dfs。
代码如下:
struct num
{
int ne;
ll l;
}k,ans[MAXN][4];
bool cmp(num a,num b)
{
return a.l>b.l;
}
void dfs1(int u)
{
int v;
FOR(i,0,3)
ans[u][i].l=0;
for(int i=0;i<q[u].size();i++)
{
v=q[u][i].ne;
if(!vis[v])
{
vis[v]=1;
dfs1(v);
ans[u][3].l=ans[v][0].l+(ll)q[u][i].l;
ans[u][3].ne=v;
sort(ans[u],ans[u]+4,cmp);
}
}
sum=max((ll)sum,ans[u][0].l+ans[u][1].l*2+ans[u][2].l);
}
void dfs2(int u)
{
int v,l;
for(int i=0;i<q[u].size();i++)
{
v=q[u][i].ne;
if(vis[v])
{
if(ans[v][0].ne!=u)
ans[u][3].l=ans[v][0].l+(ll)q[u][i].l;
else
ans[u][3].l=ans[v][1].l+(ll)q[u][i].l;
ans[u][3].ne=v;
sort(ans[u],ans[u]+4,cmp);
sum=max((ll)sum,ans[u][0].l+ans[u][1].l*2+ans[u][2].l);
break;
}
}
for(int i=0;i<q[u].size();i++)
{
v=q[u][i].ne;
l=q[u][i].l;
if(!vis[v])
{
vis[v]=1;
dfs2(v);
}
}
}
解答:
1.更新答案我们用到的是dp【当前节点】和dp【子】之和,因此dp【子】不能先改变dp【当前节点】。
2.dp【节点】的值的含义为:以该节点为根节点,得到的最长子树路径(即包含该节点及其对应子树的节点)。
3.无影响,这个是树的性质之一。



