使用java实现快速排序(挖坑填数法和指针交换法)
快速排序:通过一趟排序,将数据分为两部分,其中一部分中的所有数据比另外一部分的所有数据要小,然后按照此方法,分别对这两部分进行排序,达到最终的排序结果。
每趟排序选取基准元素,比该基准元素大的数据放在一边,比该基准元素小的数据放在另一边,这种处理方式称为分治法。
数据的移动是基准元素中比较重要的点,有两种方式实现,挖坑填数法和指针交换法。
挖坑填数法
(下图中单词有两处拼写错误,pviot和pvoit应该为pivot)
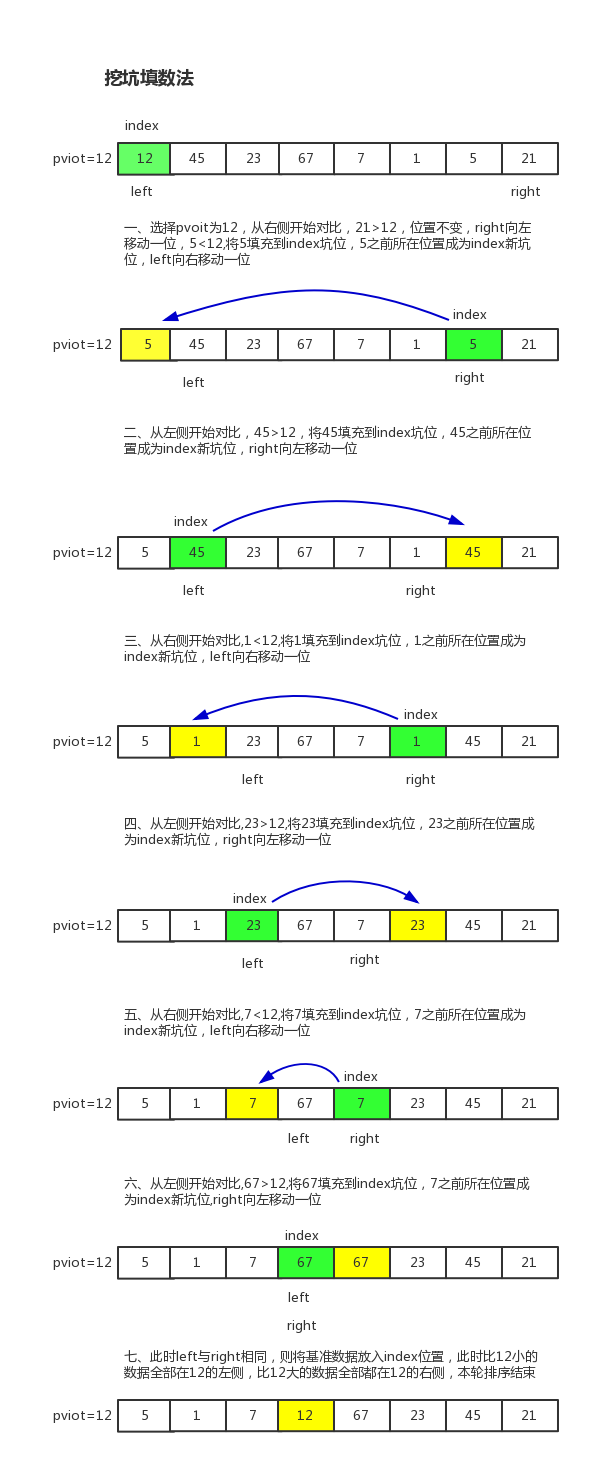
如下为代码实现
import java.util.Arrays; public class QuickSort { public static void main(String[] args) { int[] arr = { 12, 45, 23, 67, 7, 1, 5, 21 }; quickSort(arr, 0, arr.length - 1); System.out.println(Arrays.toString(arr)); } public static void quickSort(int[] arr, int startIndex, int endIndex) { if (startIndex >= endIndex) { return; } int partitionIndex = getPartitionIndex(arr, startIndex, endIndex); quickSort(arr, startIndex, partitionIndex - 1); quickSort(arr, partitionIndex + 1, endIndex); } public static int getPartitionIndex(int[] arr, int startIndex, int endIndex) { int index = startIndex; int left = startIndex; int right = endIndex; int pivot = arr[startIndex]; while (left < right) { while (left < right) { if (arr[right] < pivot) { arr[index] = arr[right]; // 找到所需值,将值填充到坑位 index = right; // 此时right位置为index新坑位 left++; // 右侧找到了数据,则left右移一位,准备进行比对 break; // 找到数据之后,跳出内循环,准备从左侧开始对比 } // 没有匹配的数据,则right左移一位,继续对比 right--; } while (left < right) { if (arr[left] > pivot) { arr[index] = arr[left]; // 找到所需的值,将值填充到坑位 index = left; // 此时left位置为index新坑位 right--; // 左侧找到了数据之后,right向左移动一位,准备进行比较 break; // 找到数据之后,跳出内循环,准备从左侧开始对比 } // 没有匹配的数据,则left右移一位,继续对比 left++; } } // 最后将pivot放入index位置 arr[index] = pivot; return index; } }
指针交换法
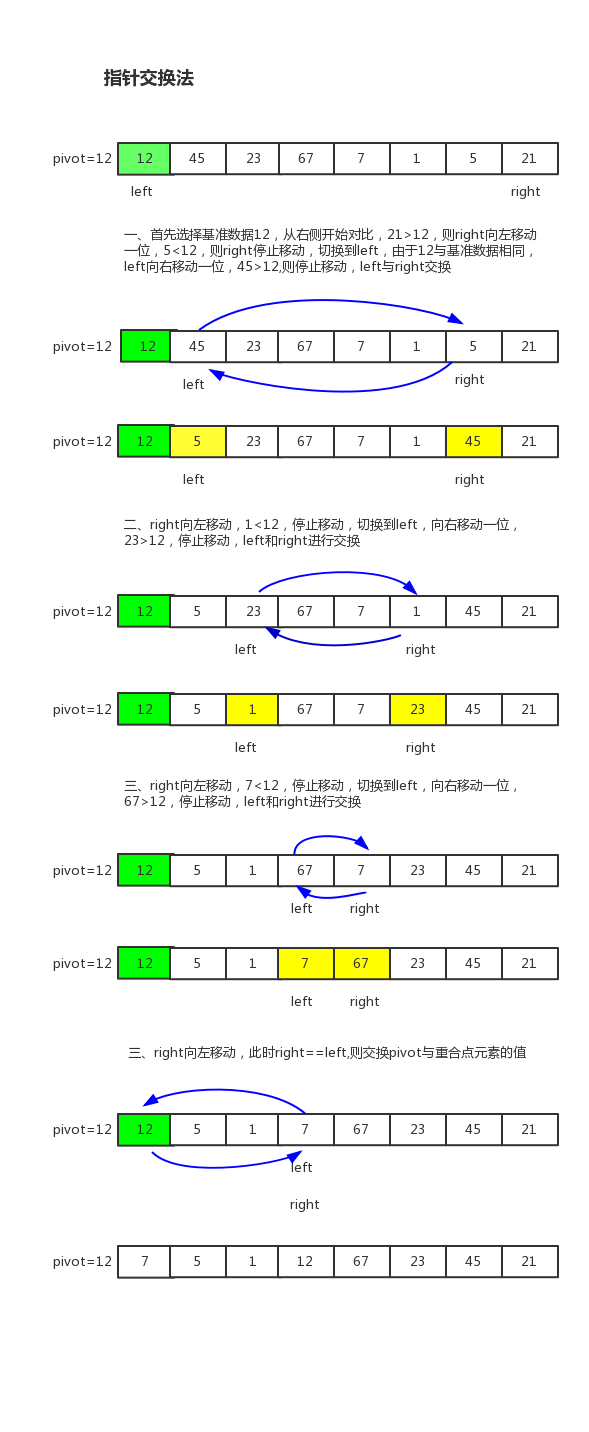
代码实现如下
import java.util.Arrays; public class QuickSort { public static void main(String[] args) { int[] arr = { 12, 45, 23, 67, 7, 1, 5, 21 }; quickSort(arr, 0, arr.length - 1); System.out.println(Arrays.toString(arr)); } public static void quickSort(int[] arr, int startIndex, int endIndex) { if (startIndex >= endIndex) { return; } int partitionIndex = getPartitionIndex(arr, startIndex, endIndex); quickSort(arr, startIndex, partitionIndex - 1); quickSort(arr, partitionIndex + 1, endIndex); } public static int getPartitionIndex(int[] arr, int startIndex, int endIndex) { int left = startIndex; int right = endIndex; int pivot = arr[startIndex]; while (left != right) { // 左侧索引必须小于右侧索引,当右侧数据大于基准元素,则将右侧元素向左移动一位,继续判断,直到找到比基准元素小的数据 while (left < right && arr[right] > pivot) { right--; } // 左侧索引必须小于右侧索引,当左侧数据小于等于基准元素,则将左侧元素右移一位,继续判断,直到找到比基准元素大的数据位置 while (left < right && arr[left] <= pivot) { // 此处必须是左侧元素“小于等于”基准元素 left++; } if (left < right) { // 通过以上两轮while循环,已经找到左侧大于基准元素的数据和右侧小于基准元素的数据,交换它们 int tmp = arr[left]; arr[left] = arr[right]; arr[right] = tmp; } } // 此时right和left值是相同的,将基准元素与重合位置元素交换 arr[startIndex] = arr[left]; arr[left] = pivot; return left; } }
讨论
1、以上两种方式只有在获取分区索引的代码不一样,其他都一样
2、指针交换法中,第二个内层while循环为什么必须要小于等于基准元素才行?
假设去掉等于,那么我们从左侧取的第一个值是12,pivot为12,则arr[left]<pivot条件不成立,那么则left的值就不会变化,此时在下面的交换中,arr[left]的值始终不变,最终的排序结果也将是错误的,所以需要是小于等于基准元素
3、以上两种方式是否有优化空间
在两种处理方式的getPartitionIndex方法返回值前添加打印数组语句,输出结果分别为
挖坑填数法输出
[5, 1, 7, 12, 67, 23, 45, 21] [1, 5, 7, 12, 67, 23, 45, 21] [1, 5, 7, 12, 21, 23, 45, 67] [1, 5, 7, 12, 21, 23, 45, 67] [1, 5, 7, 12, 21, 23, 45, 67] [1, 5, 7, 12, 21, 23, 45, 67]
指针交换法输出
[7, 5, 1, 12, 67, 23, 45, 21] [1, 5, 7, 12, 67, 23, 45, 21] [1, 5, 7, 12, 67, 23, 45, 21] [1, 5, 7, 12, 21, 23, 45, 67] [1, 5, 7, 12, 21, 23, 45, 67] [1, 5, 7, 12, 21, 23, 45, 67] [1, 5, 7, 12, 21, 23, 45, 67]
可以发现,挖坑填数法,在第三次输出时已经是一个有序集合了,指针交换法在第四次输出后也是一个有序集合,所以上述两种代码可以进行优化处理
优化,待添加。。。。。。



