详解POW工作量证明原理
原文地址 来自 微信公众号 区块链大师
POW工作量证明(英文全称为Proof of Work)早在比特币出现之前就已经有人探索,常见的是利用HASH运算的复杂度进行CPU运算实现工作量确定,当然你也可以利用卷积求导、大质数分解这些复杂的运算来达到工作量证明的目的(HASH只是pow采用一种算法而已,你可以使用大部分需要迭代运算的算法实现POW,其实稍微改一下pow算法就有可能诞生一种山寨币,然后大肆宣传欺骗小白,了解原理后就知道这并没有什么卵用),随着比特币成功后,POW为人们熟知,基于HASH的pow算法常被人误解为是pow的代名词,为了便于解释pow原理本文还是采用HASH算法作为举例。
定义
(Proof-of-work,工作量证明)最早是一个经济学名词,它是指系统为达到某一目标而设置的度量方法。简单理解就是一份证明,用来确认你做过一定量的工作。监测工作的整个过程通常是极为低效的,而通过对工作的结果进行认证来证明完成了相应的工作量,则是一种非常高效的方式
在1999年,Markus Jakobsson and Ari Juels两人将pow概念引入计算机体系,设计系统用以抵挡拒绝服务攻击和网络爬虫,后来在反垃圾邮件中被广泛使用。其设计理念是一个正常用户写一封邮件是需要一定的时间,而发送垃圾邮件者是无法接受这个等待的时间,如果pow系统能够使垃圾邮件发送者需要更多的时间来发送邮件,就可以增大他们的成本,起到抵挡攻击的作用。
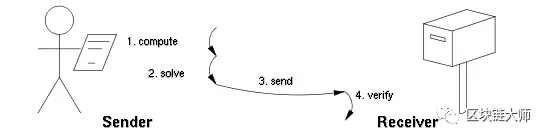
pow系统中一定有两个角色,工作者和验证者,他们需要具有以下特点:
工作者需要完成的工作必须有一定的量,这个量由工作验证者给出。
验证者可以迅速的检验工作量是否达标。
工作者无法自己"创造工作",必须由验证者发布工作。
工作者无法找到很快完成工作的办法。
pow历史
工作量证明,是一种应对拒绝服务攻击和其他服务滥用的经济对策。它要求发起者进行一定量的运算,也就意味着需要消耗计算机一定的时间。这个概念由Cynthia Dwork 和Moni Naor 1993年在学术论文中首次提出。而工作量证明(POW)这个名词,则是在1999年 Markus Jakobsson 和Ari Juels的文章中才被真正提出。
哈希运算是一种最常见的工作量证明机制,它是亚当·贝克(Adam Back)在1997年发明的,用于抵抗邮件的拒绝服务攻击及垃圾邮件网关滥用。在比特币之前,哈希现金被用于垃圾邮件的过滤,也被微软用于hotmail/exchange/outlook等产品中(微软使用一种与哈希现金不兼容的格式并将之命名为电子邮戳)。
该机制主要利用HASH运算的复杂度,通过给定的初始值,通过简单的值递增规律,利用HASH碰撞原理,直到找到特定的碰值,可以通过调节碰撞值得长度,实现对于工作量的调节(碰撞值越长,所需要的运算量越大)
哈希现金也被哈尔·芬尼以可重复使用的工作量证明(RPOW)的形式用于一种比特币之前的加密货币实验中。另外,戴伟的B-money、尼克·萨博的比特金(Bit-Gold)这些比特币的先行者,都是在哈希现金的框架下进行挖矿的。
哈希现金扫盲
哈希现金HashCash是最典型的Solution-verification实现,HashCash也是目前应用最为广泛的反垃圾邮件的pow系统。
在HashCash系统中,发件方向邮箱服务器发送的邮件信息中必须包含一段邮件签名,邮件签名中包含有收件人地址、发件时间和一个数字counter,counter需要使邮件签名满足条件:
利用SHA-1散列算法对邮件签名生成一个160-bit长度的哈希值,该哈希值前20位全为0 。此算法利用了散列算法的不可预测性,SHA-1的碰撞概率决定了算法的安全性。
在目前的认知中,发件方除了穷举尝试,无法很快的找到满足条件的签名串。于是发件方在发送邮件之前的工作就是不断地counter++生成新的邮件签名,然后获取SHA-1哈希值,判断前20位是否全为0,如果不是的话重新生成。而对于邮件服务器而言,只需要做一次SHA-1判断生成的签名是否满足条件即可,完全符合POW易于验证的定义。
算法简介
发送方签名:
counter = 0;
while(1) {
result = SHA1(mailAdress + time + counter);
if (result.substring(0, 20) == "00000000000000000000") {
break;
}
counter++;
}
sig = mailAdress + time + counter;
服务端验签:
if (SHA1(sig).substring(0, 20) == "00000000000000000000") {
return true;
}
散列函数如SHA-1是基本均匀分布的,对于我们生成的每一个邮件签名来说,对应的的哈希值在每一位上出现0和1的概率应该是相同的,SHA-1生成的160-bit哈希结果,其所有的可能是 2^160 种,而前20位固定为0的情况有 2^140 种,所以每次生成的邮件签名符合条件的概率为: 2^140 / 2^160 = 1/2^20
问题一,解空间必然存在,解空间的大小为2^140。
问题二,每一次生成邮件签名命中的概率为 1/2^20 ,客户端平均需要运算 2^20 次就能找到正确答案,运算时间为: PerSHA1Time*2^20 。
问题三,服务器端需要丢弃掉已经出现过的答案,同时需要对收件人地址和时间戳做合法性校验即可。
工作量证明系统主要特征是客户端需要做一定难度的工作得出一个结果,验证方却很容易通过结果来检查出客户端是不是做了相应的工作。这种方案的一个核心特征是不对称性:工作对于请求方是适中的,对于验证方则是易于验证的。它与验证码不同,验证码的设计出发点是易于被人类解决而不易被计算机解决。
下图表示的是工作量证明的流程:
举个例子,给定的一个基本的字符串"Hello, world!",我们给出的工作量要求是,可以在这个字符串后面添加一个叫做nonce的整数值,对变更后(添加nonce)的字符串进行SHA256哈希运算,如果得到的哈希结果(以16进制的形式表示)是以"0000"开头的,则验证通过。为了达到这个工作量证明的目标。我们需要不停的递增nonce值,对得到的新字符串进行SHA256哈希运算。按照这个规则,我们需要经过4251次计算才能找到恰好前4位为0的哈希散列。
"Hello, world!0" => 1312af178c253f84028d480a6adc1e25e81caa44c749ec81976192e2ec934c64
"Hello, world!1" => e9afc424b79e4f6ab42d99c81156d3a17228d6e1eef4139be78e948a9332a7d8
"Hello, world!2" => ae37343a357a8297591625e7134cbea22f5928be8ca2a32aa475cf05fd4266b7
...
"Hello, world!4248" => 6e110d98b388e77e9c6f042ac6b497cec46660deef75a55ebc7cfdf65cc0b965
"Hello, world!4249" => c004190b822f1669cac8dc37e761cb73652e7832fb814565702245cf26ebb9e6
"Hello, world!4250" => 0000c3af42fc31103f1fdc0151fa747ff87349a4714df7cc52ea464e12dcd4e9
通过这个示例我们对工作量证明机制有了一个初步的理解。有的人会认为如果工作量证明只是这样的一个过程,那是不是只需要记住nonce为4521计算能通过验证就行了?当然不是的,这只是一个个例。
下面,我们将输入简单的变更为"Hello, world+整数值",整数值取1到1000,也就是说,将输入变成一个由1000个值组成的数组:“Hello, world!1、Hello, world!2……Hello, world!1000”。然后对数组中的每一个输入依次进行上面例子中要求的工作量证明——找到前导为4个0的哈希散列。
容易算出,预期大概要进行216次尝试(哈希值的伪随机特性使得我们可以做概率估算),才能得到4个前导0的哈希散列。而统计一下刚才进行的1000次计算的实际计算结果,我们会发现,进行计算的平均次数为66958次,十分接近216(65536)。在这个例子中,数学期望的计算次数,就是我们要求的“工作量”,重复多次进行的工作量证明会是一个符合统计学规律的概率事件。
统计输入的字符串与对应得到目标结果实际使用的计算次数列表如下:
Hello, world!1 => 42153
Hello, world!2 => 2643
Hello, world!3 => 32825
Hello, world!4 => 250
Hello, world!5 => 7300
...
Hello, world!995 => 164819
Hello, world!996 => 178486
Hello, world!997 => 22798
Hello, world!998 => 68868
Hello, world!999 => 46821
比特币体系里的工作量证明机制与上述示例类似,但要比它更复杂一些,以后会另起文章说明