字符串算法

HASH

个人理解：将字符串(...)通过自定义的运算方式转换为数字(...)。这样处理起来更加快捷，也节省内存空间。

怎样$HASH$？我个人是按数字的进制方法处理的。

例子：一串由小写字母组成的字符串，我们可将其视作一个二十六(或更大)进制的数字，各位上的字母$['a'...'z']$分别对应数字$[0...25]$。

如$abcdc=0\times 26^{4}+1\times 26^{3}+2\times 26^{2}+3\times 26^{1}+2\times 26^{0}$

 

KMP

在文本串($s$)中寻找给定的模式串($s1$)。

设当前$s1[1...j]$已经与$s[i-j+1...i]$完全匹配。

这时$s1[j+1]$不等于$s[i+1]$，无法继续匹配。我们要调整模式串$s1$的位置，但我们不暴力地一位位移动。

我们要预处理一个$nxt$数组。设$nxt[j]=k$,使$s1[1...k]$与$s1[j-k+1...j]$按位相等。如果在$j+1$位失配了，就将$j$指向$nxt[j]$。(显然$nxt[j]$越大越有利）

//因为 $s1[j-k+1...j]$与 $s[i-k+1...i]$匹配，而 $s1[1...k]$又与 $s1[j-k+1...j]$按位相等，所以易得 $s1[1...k]$与 $s[i-k+1...i]$匹配。

例子：$s1=$'$ababab$'，$nxt[1...6]=[0,0,1,2,3,2]$。

代码实现 (a为文本串，b为模式串)

void KMP() {
    int j=0;
    for(int i=1;i<=n;i++) { //n=strlen(a+1)
        while(j&&a[i]!=b[j+1]) j=nxt[j];
        if(a[i]==b[j+1]) j++;
        if(j==m) ans++,j=nxt[j];
    }
}

预处理$nxt$数组，就是模式串“自我匹配”的过程啦！（代码和上面很像）

void GetNXT() {
    nxt[1]=0; 
    int j=0;
    for(int i=2;i<=m;i++) { //m=strlen(b+1)
        while(j&&b[i]!=b[j+1]) j=nxt[j];
        if(b[i]==b[j+1]) j++;
        nxt[i]=j;
    }
}

 

Trie字典树

我们有六个字符串：'$inn$','$a$','$to$','$tea$','$ted$','$ten$'。将它们建成一棵Trie字典树是这样的：

 

 

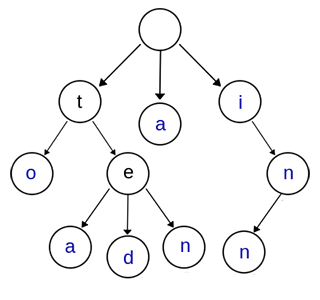
 这个很好理解的，直接放代码了(有详细注释～)

struct TrieTree {
    int tot,c[N][Z]; //Z为字符集大小 
    //tot:字典树的节点总数，c[i][j]:i号节点下j字符的节点编号
    bool bo[N]; //bo[i]:i号节点是否为一个字符串的结尾
    void clear() { //字典树的初始化
       tot=0;
       memset(c,0,sizeof(c));
       memset(bo,false,sizeof(bo));
    }
    void insert(char *s) { //在字典树中插入字符串s
       int len=strlen(s),u=0; //u:当前所在的节点编号(现为根节点0)
       for(int i=0;i<len;i++) {
            int v=s[i]-'0'; 
            if(!c[u][v]) c[u][v]=++tot; //没有此节点则新建一个
            u=c[u][v]; //顺着字典树向下走
       } 
       bo[u]=1; //记录u号节点为一个字符串的结尾
    }
    bool search(char *s) { //查询字符串s是否为给定字符串集合中某个串的前缀
        int len=strlen(s),u=0;
        for(int i=0;i<len;i++) {
            int v=s[i]-'0';
            if(!c[u][v]) return 0; //没有此节点，返回false
            u=c[u][v]; //顺着字典树向下走
        }
        return 1; //找到了，返回true
    }
};

 

AC自动机

前置技能：KMP、Trie字典树 (就在上面

AC自动机的功能还是在给定的文本串中寻找模式串。不同于KMP的是，这次的模式串不止一个。

看着代码，画图理解吧。

struct Aho_Corasick_Automaton {
    int tot,c[N][26],val[N],fail[N];
    void clear() {
        tot=0;
        memset(c,0,sizeof(c));
        memset(val,0,sizeof(val));
    }
    void insert(char *s) {
        int len=strlen(s),u=0;
        for(int i=0;i<len;i++) {
            int v=s[i]-'a';
            if(!c[u][v]) c[u][v]=++tot;
            u=c[u][v];
        }
        val[u]++;
    }
    void find() {
        for(int i=0;i<26;i++) 
         if(c[0][i]) fail[c[0][i]]=0,q.push(c[0][i]);
        while(!q.empty()) {
            int u=q.front(); q.pop();
            for(int i=0;i<26;i++) 
             if(c[u][i]) 
              fail[c[u][i]]=c[fail[u]][i],q.push(c[u][i]);
             else c[u][i]=c[fail[u]][i];
        }
    }
    int query(char *s) {
        int len=strlen(s),u=0,ans=0;
        for(int i=0;i<len;i++) {
            u=c[u][s[i]-'a'];
            for(int v=u;v&&~val[v];v=fail[v]) 
             ans+=val[v],val[v]=-1;
        }
        return ans;
    }
};

 

完结撒花 //虽然烂尾了