『一本通』二分与三分

传送门：《信息学奥赛一本通》提高版题解索引

---

 

愤怒的牛

#include<bits/stdc++.h>
using namespace std;
int n,m,ans,a[100005];

int check(int x) {
    int cnt=1,lst=a[1];
    for(int i=2;i<=n;i++)
     if(a[i]-lst>=x) cnt++,lst=a[i];
    return cnt;
}

int main() {
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    sort(a+1,a+n+1);
    int l=1,r=a[n]-a[1];
    while(l<=r) {
        int Mid=l+r>>1;
        if(check(Mid)>=m) l=Mid+1,ans=Mid;
        else r=Mid-1;
    }
    printf("%d",ans);
}

 

Best Cow Fences

#include<bits/stdc++.h>
#define N 100005
using namespace std;
int n,L,ans,a[N];
long long s[N];

bool check(int x) {
    for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i]-x;
    long long Min=0;
    for(int i=L;i<=n;i++) {
        Min=min(Min,s[i-L]);
        if(s[i]>=Min) return 1;
    }
    return 0;
}

int main() {
    scanf("%d%d",&n,&L);
    int l=0,r=0;
    for(int i=1;i<=n;i++) {
        scanf("%d",&a[i]);
        a[i]*=1000,r=max(r,a[i]);
    } 
    while(l<=r) {
        int Mid=l+r>>1;
        if(check(Mid)) l=Mid+1,ans=Mid;
        else r=Mid-1;
    }
    printf("%d",ans);
}
/*
二分枚举平均值ave。
将每个数减去ave，看是否有长度不小于L的连续区间，使得这段区间的和大于等于0。
*/

 

数列分段II

#include<bits/stdc++.h>
using namespace std;
int n,m,a[100005];

bool check(int x) {
    int cnt=1,sum=a[1];
    for(int i=2;i<=n;i++) {
        sum+=a[i];
        if(sum>x) cnt++,sum=a[i];
        if(cnt>m) return 0;
    } return 1;
}

int main() {
    scanf("%d%d",&n,&m);
    int l=0,r=0;
    for(int i=1;i<=n;i++) {
        scanf("%d",&a[i]);
        l=max(l,a[i]),r+=a[i];
    }
    while(l<=r) {
        int Mid=l+r>>1;
        if(check(Mid)) r=Mid-1; 
        else l=Mid+1;
    }
    printf("%d",l);
}
//二分答案

 

曲线

#include<bits/stdc++.h>
#define eps 1e-10
using namespace std;
int T,n;
struct node{double a,b,c;}s[100005];

double F(double x) {
    double f=-1e10;
    for(int i=1;i<=n;i++)
     f=max(f,s[i].a*x*x+s[i].b*x+s[i].c);
    return f;
}

int main() {
    T=read();
    while(T--) {
        n=read();
        for(int i=1;i<=n;i++)
         s[i]=(node){read(),read(),read()};
        double l=0,r=1000;
        while(l+eps<=r) {
            double Mid=(l+r)/2;
            if(F(Mid)>=F(Mid+eps)) l=Mid;
            else r=Mid;
        }
        printf("%.4lf\n",F(l));
    }
}
//二分枚举x

 

 扩散

#include<bits/stdc++.h>
#define N 55
using namespace std;
int T,n,ans,x[N],y[N],fa[N];
int find(int x) {return fa[x]==x?x:fa[x]=find(fa[x]);}

bool check(int t) {
    for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=1;i<n;i++)
     for(int j=i+1;j<=n;j++) {
        int d=abs(x[i]-x[j])+abs(y[i]-y[j]); //曼哈顿距离
        if(d<=2*t) { //不超过时间的2倍（两个点都能扩散） 
            int fi=find(i),fj=find(j);
            if(fi!=fj) fa[fi]=fj;
        }
     }
    int tot=0;
    for(int i=1;i<=n;i++) if(fa[i]==i) tot++;
    if(tot==1) return 1; //如果只有一个联通块 
    return 0;
}

int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d%d",&x[i],&y[i]);
    int l=0,r=1e9;
    while(l<=r) { //二分答案 
        int Mid=l+r>>1;
        if(check(Mid)) r=Mid-1,ans=Mid;
        else l=Mid+1;
    }
    printf("%d",ans);
}

 

灯泡

 

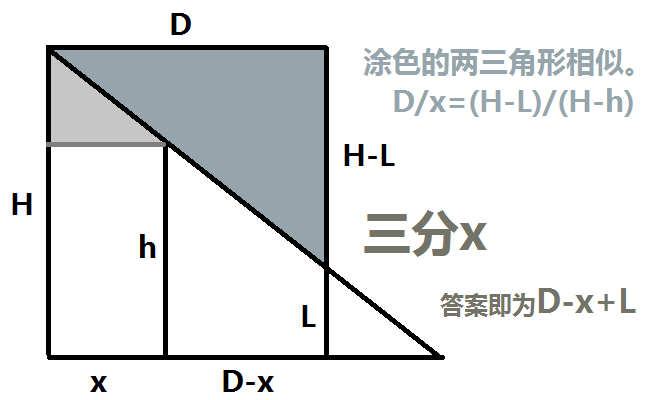
#include<bits/stdc++.h>
#define eps 1e-8 
using namespace std;
int T;
double D,H,h;
double F(double x) {return D-x+H-(H-h)*D/x;} 

int main() {
    scanf("%d",&T);
    while(T--){
        scanf("%lf%lf%lf",&H,&h,&D);
        double l=D*(H-h)/H,r=D; //或 l=D-D*h/H
        while(r-l>eps) {
            double M1=(l+r)/2.0;
            double M2=(M1+r)/2.0;
            if(F(M1)<F(M2)) l=M1; else r=M2;
        }
        printf("%.3lf\n",F(l));
    }
}

 

传送带

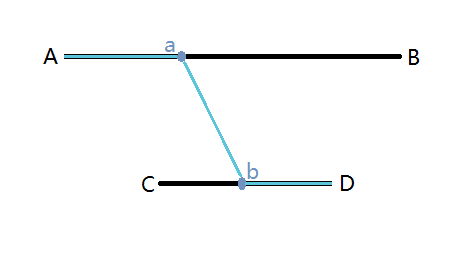
#include<bits/stdc++.h>
#define eps 1e-6
using namespace std;
int P,Q,R;
struct node{double x,y;}A,B,C,D,a,b;
double dis(node a,node b) {
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

double cal(double p1,double p2) {
    a.x=A.x+(B.x-A.x)*p1;
    a.y=A.y+(B.y-A.y)*p1;
    b.x=C.x+(D.x-C.x)*p2;
    b.y=C.y+(D.y-C.y)*p2;
    return dis(A,a)/P+dis(a,b)/R+dis(b,D)/Q;
}

double get(double x) {
    double l=0,r=1;
    while(r-l>eps) {
        double M1=l+(r-l)/3.0,M2=r-(r-l)/3.0;
        if(cal(x,M1)>cal(x,M2)) l=M1; else r=M2;
    }
    return cal(x,l);
}

int main() {
    cin>>A.x>>A.y>>B.x>>B.y;
    cin>>C.x>>C.y>>D.x>>D.y;
    cin>>P>>Q>>R;
    double l=0,r=1;
    while(r-l>eps) {
        double M1=l+(r-l)/3.0,M2=r-(r-l)/3.0;
        if(get(M1)>get(M2)) l=M1; else r=M2;
    }
    printf("%.2lf",get(l));
}
//三分(a点)套三分(b点) 

 

完结 (2019.1.29)