DS博客作业05--查找
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
| 姓名 | 付峻霖 |
0.PTA得分截图

1.本周学习总结(0-5分)
1.1 查找的性能指标
ASL(Average Search Length)
在查找运算中,由于所费时间在关键字的比较上,所以把平均需要和待查找值比较的关键字次数称为平均查找长度。
- 公式:ASL=∑ni=1pici
- ASL是平均查找次数,在期末考中就考了一题哈希表,可以计算查找成功和查找不成功的平均查找长度,ASL可以很直观的计算出查找的效率
1.2 静态查找
1.2.1 顺序查找
- 顺序查找定义
就从头遍历到尾部一个一个找,找到待查找元素即查找成功,若到尾部没有找到,说明查找失败
- 顺序表的结构体定义
typedef int ElemType; /* ElemType类型根据实际情况而定,这里假设为int */
typedef struct
{
ElemType data[MAXSIZE]; /* 数组,存储数据元素 */
int length; /* 线性表当前长度 */
}SqList;
- 代码实现
/* 初始条件:顺序线性表L已存在 */
/* 操作结果:返回L中第1个与e满足关系的数据元素的位序。 */
/* 若这样的数据元素不存在,则返回值为0 */
int LocateElem(SqList L,ElemType e)
{
int i;
if (L.length==0)
return 0;
for(i=0;i<L.length;i++) /* 遍历顺序表 */
{
if (L.data[i]==e) /* 找到了 */
break;
}
if(i>=L.length)
return 0;
return i+1;
}
- ASL分析
成功:从头查找到尾,因此平均查找次数为(1+2+3..+n)/n=(n+1)/2
不成功:从头找到尾都没有找到,因此查找次数就为表的长度n
1.2.2 二分查找
- 要求是顺序表,根据顺序表构建二叉树,中间数为根,左小右大,也就是判定树
- 例如
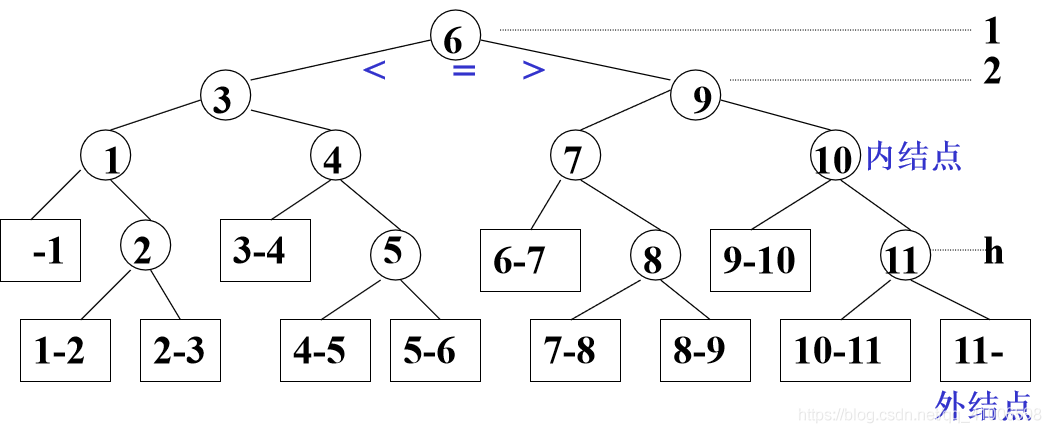
如图,根据判定树求解,假设每个元素的查找概率相等,则查找成功时的ASL=(11+22+43+44)/11。第一层的一个数比较成功时所需比较次数一次,第二层的两个数需要两次,依此类推。即查找成功时比较次数:为该结点在判定树上的层次数,不超过树的深度d=log2n+1, 查找不成功的过程就是走了一条从根结点到外部结点的路径d或d-1。 - 时间复杂度
每次查找后,范围缩小一半,因此时间复杂度为O(logn) - ASL分析
成功=每一层节点数层次数的总和/总结点数
不成功=其他不存在于树中的每一层节点数(层次数-1)/总结点数
1.3 二叉搜索树
二叉排序树的定义:
1.或者是空树
2.或者是满足以下性质的二叉树
★若它的左子树不空,则左子树上的所有关键字的值均小于根关键字的值
★若它的右子树不空,则右子树上的所有关键字的值均大于根关键字的值
1.3.1 如何构建二叉搜索树(操作)
- 结合一组数据介绍构建过程
设有一个输入数据的序列是 { 46, 25, 78, 62, 12, 80 }, 试画出从空树起,逐个输入各个数据而生成的二叉搜索树。

- 二叉搜索树的ASL成功和不成功的计算方法。
★ASL成功=每个结点的高度相加/结点总数
例如:
☆ 5,4,3,2,1 五个关键字
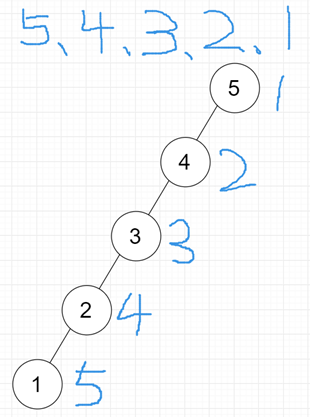
ASL=(1+2+3+4+5)/5=3
☆ 3,4,5,2,1关键字
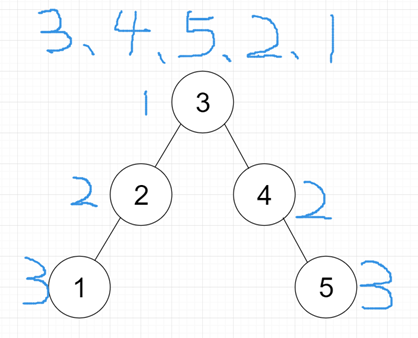
ASL=(1+2+2+3+3)/5=2.2
★ASL不成功=其他不存在于树中的每一层节点数(层次数-1)/总结点数
例如:

1.3.2 如何构建二叉搜索树(代码)
- 结构体定义
/* 二叉树的二叉链表结点结构定义 */
typedef struct BiTNode /* 结点结构 */
{
int data; /* 结点数据 */
struct BiTNode *lchild, *rchild; /* 左右孩子指针 */
} BiTNode, *BiTree;
- 二叉搜索树的构建操作
void CreateBST(BiTree *T, int n)/*建树函数*/
{
int x;
BiTree T=NULL;//树初始化为空
for (int i = 0; i < n; i++)
{
cin >> x;
InsertBST(&T, x);
}
}
- 二叉搜索树的插入操作
/* 当二叉排序树T中不存在关键字等于key的数据元素时, */
/* 插入key并返回TRUE,否则返回FALSE */
int InsertBST(BiTree *T, int key)
{
BiTree p,s;
if (!SearchBST(*T, key, NULL, &p)) /* 查找不成功 */
{
s = (BiTree)malloc(sizeof(BiTNode));
s->data = key;
s->lchild = s->rchild = NULL;
if (!p)
*T = s; /* 插入s为新的根结点 */
else if (key<p->data)
p->lchild = s; /* 插入s为左孩子 */
else
p->rchild = s; /* 插入s为右孩子 */
return TRUE;
}
else
return FALSE; /* 树中已有关键字相同的结点,不再插入 */
}
- 二叉搜索树的删除操作
/* 从二叉排序树中删除结点p,并重接它的左或右子树。 */
int Delete(BiTree *p)
{
BiTree q,s;
if((*p)->rchild==NULL) /* 右子树空则只需重接它的左子树(待删结点是叶子也走此分支) */
{
q=*p; *p=(*p)->lchild; free(q);
}
else if((*p)->lchild==NULL) /* 只需重接它的右子树 */
{
q=*p; *p=(*p)->rchild; free(q);
}
else /* 左右子树均不空 */
{
q=*p; s=(*p)->lchild;
while(s->rchild) /* 转左,然后向右到尽头(找待删结点的前驱) */
{
q=s;
s=s->rchild;
}
(*p)->data=s->data; /* s指向被删结点的直接前驱(将被删结点前驱的值取代被删结点的值) */
if(q!=*p)
q->rchild=s->lchild; /* 重接q的右子树 */
else
q->lchild=s->lchild; /* 重接q的左子树 */
free(s);
}
return TRUE;
}
- 分析代码的时间复杂度
时间复杂度:最好:O(logn),最坏:O(n) - 为什么要用递归实现插入、删除?递归优势体现在代码哪里?
1.递归可以使算法大大简化,代码足够精简(意味着不好理解)
2.保留父子关系,便于删除和插入顺利找到父亲和孩子
1.4 AVL树
-
1.AVL树解决什么问题,其特点是什么?
★AVL能解决二叉搜索树存在数据分配不平衡的问题,她将二叉搜索树调整为经可能的矮,这样平均查找长度越小,查找速度越快。
★平衡二叉树是二叉排序树的改进版,也就是说平衡二叉树是二叉排序树的一个特殊情况
★我们将每个结点的平衡因子的绝对值都不超过1的二叉排序树称为平衡二叉树
★平衡因子:左子树高度-右子树高度 -
2.结合一组数组,介绍AVL树的4种调整做法。
输入关键字序列{16,3,7,11,9,26,18,14,15},构造一颗AVL树。 有调整要写成调整类型及结果

no picture you say a J8,4种调整做法图中已经画的非常清楚了,我这就不再进行过多的文字赘述 -
3.AVL树的高度和树的总节点数n的关系?
高度为 h 的 AVL 树,最多为满二叉树,节点数 N 最多2^h − 1; 最少类似于斐波那契数列,满足N(h)=N(h− 1) +N(h− 2) + 1 的计算公式 -
4.介绍基于AVL树结构实现的STL容器map的特点、用法。
Map是STL的一个关联容器,翻译为映射,数组也是一种映射。如:int a[10] 是int 到 int的映射,而a[5]=25,是把5映射到25。数组总是将int类型映射到其他类型。这带来一个问题,有时候希望把string映射成一个int ,数组就不方便了,这时就可以使用map。map可以将任何基本类型(包括STL容器)映射到任何基本类型(包括STL容器)。
★可调用函数
begin() 返回指向map头部的迭代器
end() 返回指向map末尾的迭代器
rbegin() 返回一个指向map尾部的逆向迭代器
rend() 返回一个指向map头部的逆向迭代器
lower_bound() 返回键值>=给定元素的第一个位置
upper_bound() 返回键值>给定元素的第一个位置
empty() 如果map为空则返回true
max_size() 返回可以容纳的最大元素个数
size() 返回map中元素的个数
clear() 删除所有元素
count() 返回指定元素出现的次数
equal_range() 返回特殊条目的迭代器对
erase() 删除一个元素
swap() 交换两个map
find() 查找一个元素
get_allocator() 返回map的配置器
insert() 插入元素
key_comp() 返回比较元素key的函数
value_comp() 返回比较元素value的函数
1.5 B-树和B+树
1.5.1 B-树和AVL树区别,其要解决什么问题?
★AVL树结点仅能存放一个关键字,树的高度较高,而B-树的一个结点可以存放多个关键字,降低了树的高度,可以解决大数据下的查找
1.5.2 B-树定义。结合数据介绍B-树的插入、删除的操作,尤其是节点的合并、分裂的情况
- B-树定义
也叫B树,即平衡多路查找树,m阶B树表示节点可拥有的最多m个孩子,2-3树是3阶B树,2-3-4树是4阶B树。多叉树可以有效降低树的高度,h=log_m(n),m为log的底数。
★一颗m阶的B树需要满足下列条件:
①每个结点最多有m-1个关键字。
②根结点最少可以只有1个关键字。
③非根结点至少有m/2-1个关键字。
④每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
⑤所有叶子结点都位于同一层,或者说根结点到每个叶子结点的长度都相同。
- B-树的插入
★思路:插入的时候,我们需要记住一个规则:判断当前结点key的个数是否小于等于m-1,如果满足,直接插入即可,如果不满足,将节点的中间的key将这个节点分为左右两部分,中间的节点放到父节点中即可。
★举例:在5阶B树中,结点最多有4个key,最少有2个key(注意:下面的节点统一用一个节点表示key和value)。
插入18,70,50,40
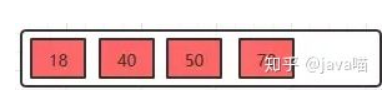
插入22
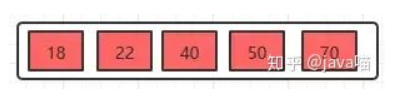
插入22时,发现这个节点的关键字已经大于4了,所以需要进行分裂
分裂后结果如下
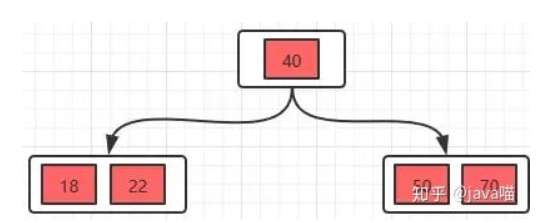
接着再分别插入23,25,39
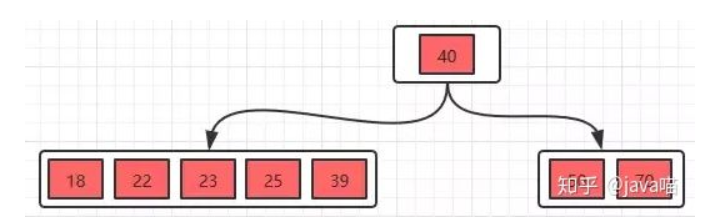
分裂后,得到最终结果
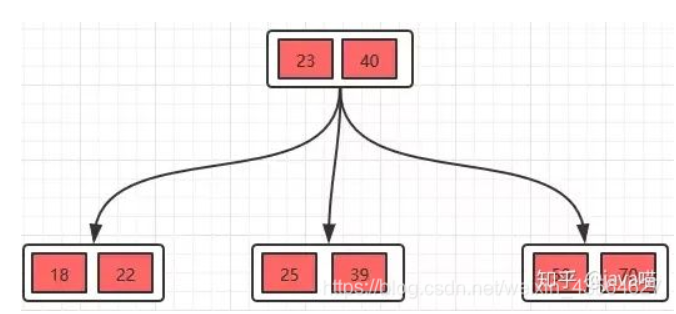
- B-树的删除
★思路:在B-树中删除节点时,可能会发生向兄弟节点借元素,和孩子节点交换元素,甚至节点合并的过程。
★举例:我们以下面的5阶树为基础,每个节点内元素个数为2~4个,依次删除8、16、15、4这4个元素。
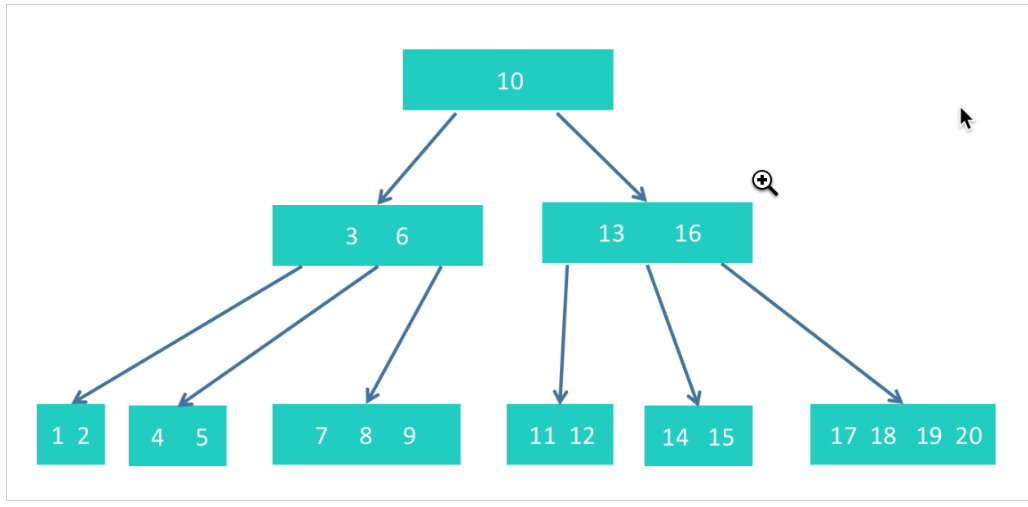
删除8,因为删除8后,不破坏树的性质,所以直接删除即可。
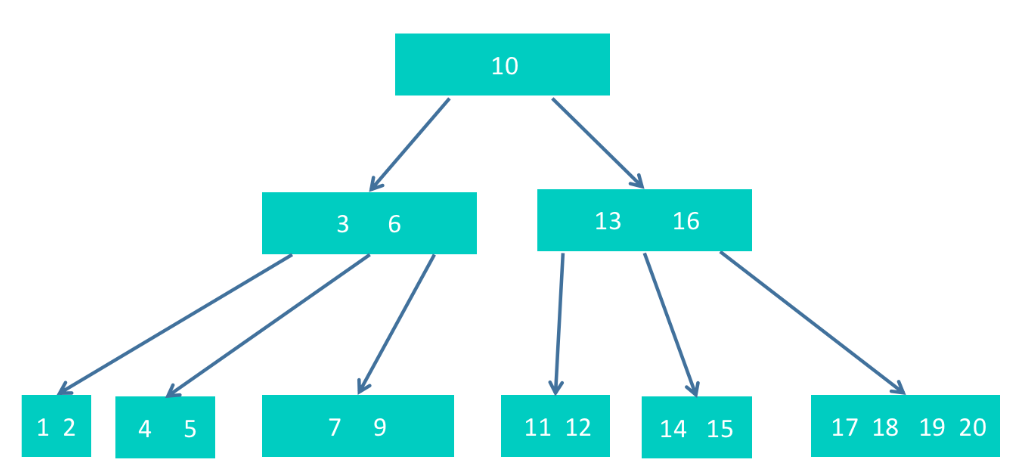
然后删除16,这导致该节点只剩下一个13节点,不满足节点内元素个数为2~4个的要求了。所以需要调整。这里可以向孩子借节点,把17提升上来即可,得到下图。这里不能和兄弟节点借节点,因为从3,6节点中把6借走后,剩下的3也不满要求了。另外,也不能把孩子中的15提升上来,那样会导致剩下的14不满足要求。

然后删除15,删除15后同样需要调整。调整的方式是,18上升,17下降到原来15的位置,得到下图。
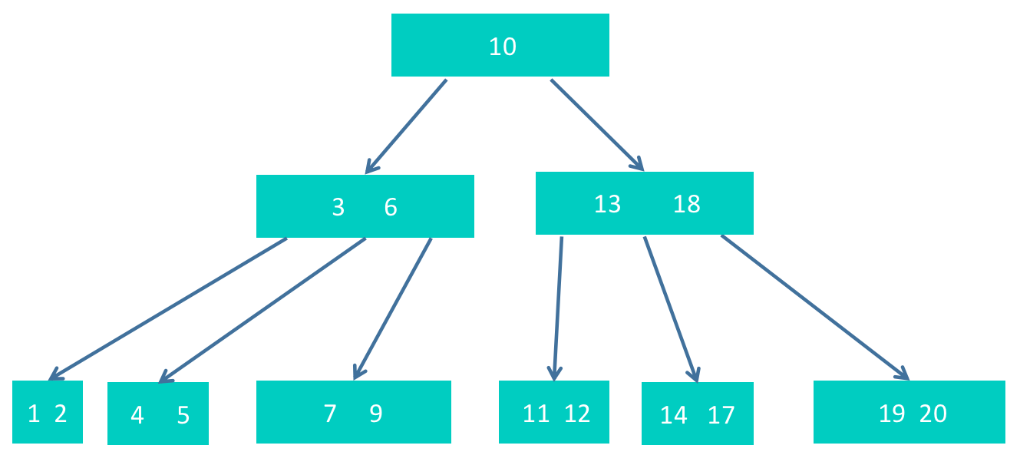
然后删除元素4,删除4后该节点只剩下5,需要调整。可是它的兄弟节点也都没有多余的节点可借,所以需要进行节点合并。节点合并时,方式会有多种,我们选择其中的一种即可。这里,我们选择父节点中的3下沉,和1,2,以及5进行合并,如下图。

这次调整后,导致6不符合要求了。另外,6非根节点,但只有2个孩子,也不符合要求。需要继续调整。调整的方式是,将10下沉,和6,以及13,18合并为根节点
调整完后得到最终结果
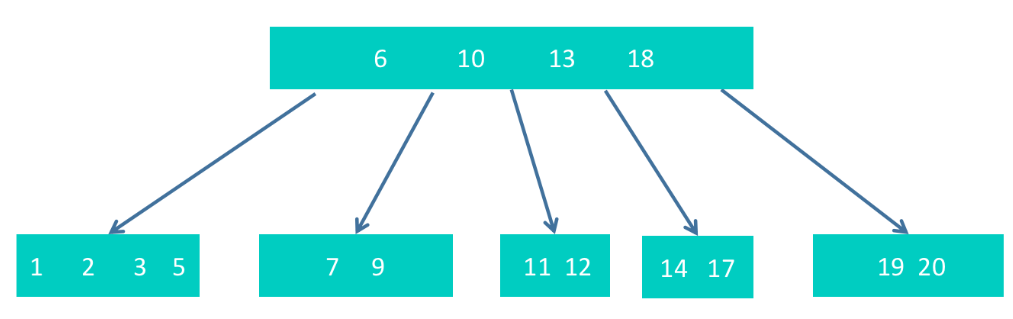
1.5.3 B+树定义,其要解决问题
- B+树定义
B+树是应数据库所需而出现的一种 B 树的变形树。
★一棵m阶的B+树需要满足下列条件:
①每个分支结点最多有m棵子树(子结点)
②非叶根结点至少有两棵子树,其他每个分支结点至少有m/2棵子树
③结点的子树个数与关键字个数相等
④所有叶结点包含全部关键字及指向相应记录的指针,而且叶结点中将关键字按大小顺序排列,并且相邻叶结点按大小顺序相互链接起来。
⑤所有分支结点(可看成是索引的索引)中仅包含它的各个子结点(即下一级的索引块)中关键字的最大值及指向其子结点的指针
- 解决的问题
①B树只适合随机检索,B+树同时支持随机检索和顺序检索,因此B+树比B树更适合实际应用中操作系统的文件索引和数据库索引 **
②数据库索引要采用B+树,因为B+树的叶子节点使用指针顺序连接在一起,只要遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的,而B树效率太低**。
1.6 散列查找。
1.6.1 哈希表的设计主要涉及哪几个内容?
- 定义
哈希表又叫散列表,是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
- 哈希函数常用构造方法
- 直接定址法
直接定址法是以关键字k本身加上某个常数c作为哈希地址的方法。
哈希函数为h(k)=k+c
该方法的特点是哈希函数计算简单,若关键字分布不连续将造成内存单元大量浪费。 - 除留取余法
除留余数法是用关键字k除以某个不大于哈希表长度m的整数p所得的余数作为哈希地址。
哈希函数为h(k)=k mod p
该方法选取的p最好为不大于m的素数,从而尽量减少发生哈希冲突的可能性。
1.6.2 结合数据介绍哈希表的构造及ASL成功、不成功的计算
例如关键字序列{18,2,10,6,78,56,45,50,110,8}这样一组数据,散列函数为:H(key)=key)mod 11,处理冲突采用线性探测法,装填(载)因子为0.77。
首先根据装填因子求出散列表长度为13,画图后,对每个关键字取余11,把他们一个一个放到散列表中,如果有冲突,则采取线性探测法
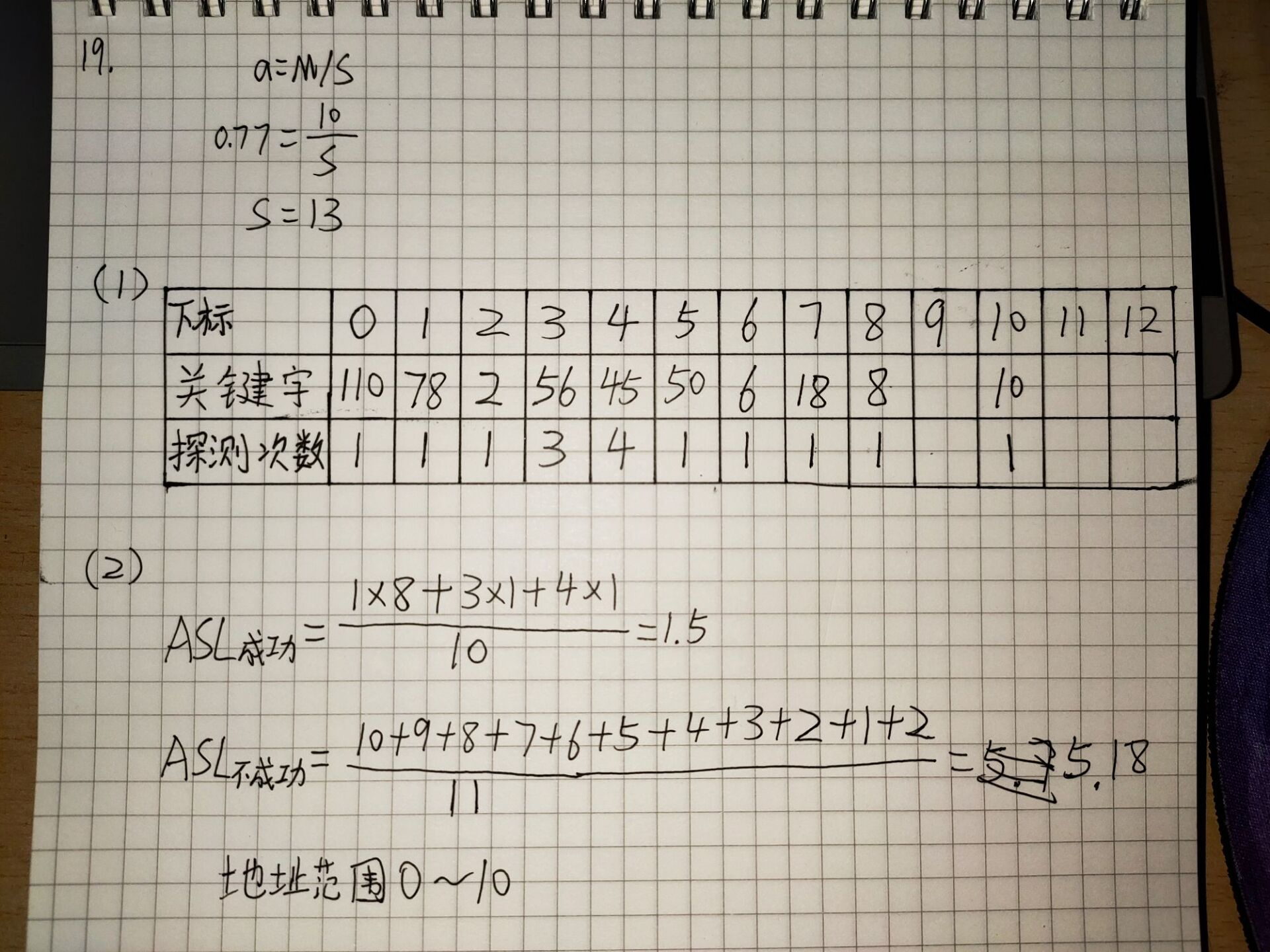
1.6.3 结合数据介绍哈希链的构造及ASL成功、不成功的计算
例如关键字序列(25,10,8,27,32,68)这样一组数据,散列表的长度为8,散列函数H(k)=k mod 7
用链地址法的好处是不会存在冲突的现象,当出现俩数据取余后的值相同时,则头插法插在同一条链上。

2.PTA题目介绍(0--5分)
2.1 是否完全二叉搜索树(2分)
- 什么是完全二叉搜索树呢?
通俗点来讲,就是完全二叉树+二叉搜索树,需要同时满足这两种树的条件,所以要求
①生成结点的顺序是严格按照从上到下,从左往右的顺序来构建的二叉树。
②任意一个结点,左子树所有结点的键值要大于结点,右子树所有结点的键值要小于结点 - 判断一棵树是否是完全二叉树的基本思路
①如果树为空,则直接返回错
②如果树不为空:层序遍历二叉树
★如果一个结点左右孩子都不为空,则pop该节点,将其左右孩子入队列;
★如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
★如果遇到一个结点,左孩子不为空,右孩子为空;或者左右孩子都为空;则该节点之后的队列中的结点都为叶子节点;该树才是完全二叉树,否则就不是完全二叉树;
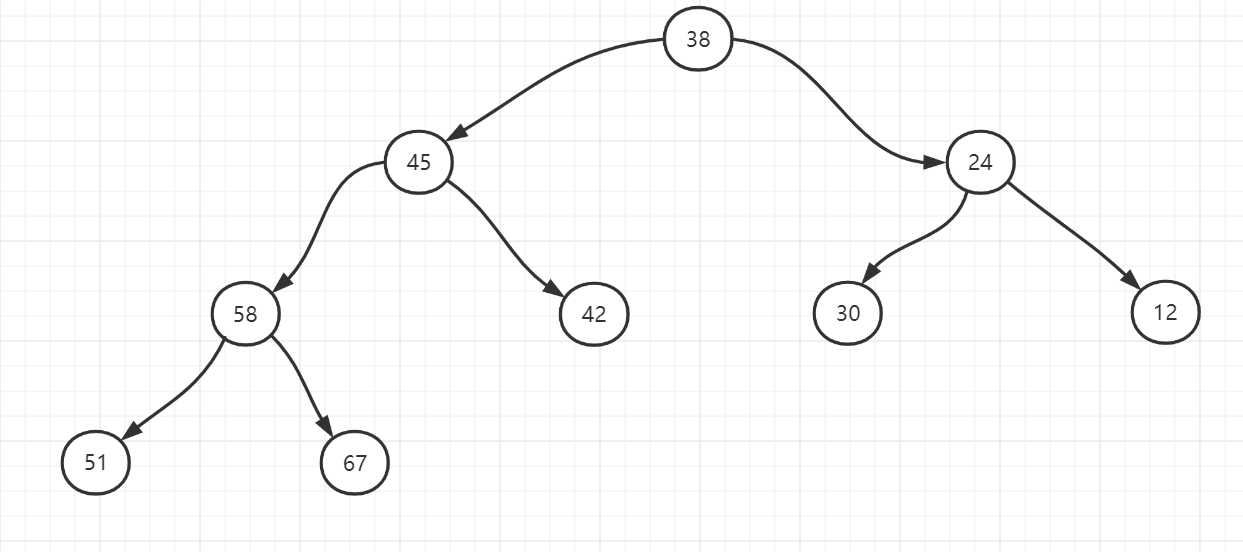
如图所示上面这种从上到下,从左到右依次构建二叉树,并且满足二叉搜索树的条件,这样的树就是完全二叉搜索树。

而这种,就不是了,因为不满足完全二叉树的条件:从上到下,从左到右依次构建二叉树。
2.1.1 伪代码(贴代码,本题0分)
int levelOrder(BinTree t) //层序遍历并判断完全二叉树
{
如果是空树
打印“空”
根结点入队列
while (队列有东西时)
if (队列读取到空结点)
flag = 1;//表示接下来不再统计结点数
else //队列头结点非空
打印队头元素
if (flag == 0)
结点数++; //统计结点数
左结点入队列
右结点入队列
队列头出队列
return 结点数;
}
2.1.2 提交列表

2.1.3 本题知识点
①用了层次遍历,因此要借用了队列来存储树中的结点
②调用了队列的相关库函数,q.push(),q.front(),q.pop()等等
③关于完全二叉搜索树概念的理解:完全+搜索
2.2 航空公司VIP客户查询(2分)
2.2.1 伪代码(贴代码,本题0分)
int main()
{
for (循环输入n条数据)
输入输入身份证,已行驶里程数据
if (里程小于最小里程)
低于最低里程按最低里程k计算
if (若该身份证已被登记为会员)
增加里程数
else(未被登记为会员)
则现在输入身份证及里程信息
for (M行查询人的身份证号码)
输入身份证
if (该身份正存在,则输出)
则输出
else 该身份不存在
输出"No Info"
}
2.2.2 提交列表
2.2.3 本题知识点
①哈希表的运用。利用哈希表来存放结点所在下标。
②调用了图的库函数,用M.count(id)求数组M中下标为id的数据是否存在
③map<string,int>M
④调用max(a,b)函数来求a b中的较大值
2.3 基于词频的文件相似度(1分)
2.3.1 伪代码(贴代码,本题0分)
int main() {
for(遍历文件) {
while(读取一行文本 碰到#就停止)
令top=0来分割字符串
for(将一行的字符串进行划分)
if(不是字母,即为分割符)
if(单词小于3,不记录)
top=0;
跳过本次循环
if(单词大于10)
只记录前十
else
加结束符
单词数+1
else 是字母,
就把所有 大写改小写
本行的最后一个单词还没有进行判断,需要单独判断一下
//计算相似度
for(遍历查询总数)
输入一对文件编号
map<string,int>::iterator it1,it2;//两个迭代器,类似指针
分子,分母=两个文件所有单词-相同的
for(同时对两个文件遍历 )
if(it1比it2小)
it1++向后移动
else if(it2比it1小)
it2++向后移动
else it2等于it1
都向后移动
}
2.3.2 提交列表

2.3.3 本题知识点
①调用了图的库函数
②利用getchar()吸收回车
③使用了迭代器


