DS博客作业03--树
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
| 姓名 | 付峻霖 |
0.PTA得分截图

1.本周学习总结
1.1 二叉树结构
二叉树是n个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根结点和两颗互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
1.1.1 二叉树结构
- 特点:
- 二叉树,顾名思义每个结点最多有两颗子树
- 左子树和右子树是有顺序的,次序不能任意颠倒
- 即使树中某结点只有一颗子树,也要区分它是左子树还是右子树
- 二叉树的五种基本形态
- 空二叉树
- 只有一个根结点
- 根结点只有左子树
- 根结点只有右子树
- 根结点:我都有
- 性质
- 在二叉树的第i层最多有2^(i-1)个结点
- 深度为k的二叉树最多有2^k-1个结点
- 对任何一颗二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
- 具有n个结点的完全二叉树的深度为[log(2,n)]min+1
- 如果有一棵有n个结点的完全二叉树(其深度为[log2n]min+1)的结点按层次序编号(从左到右,从上到下),则对任一结点i(1<=i<=n)有
(1)如果i=1,则结点 i 是二叉树的根,无双亲;如果i>1,则其双亲是结点 [i/2]min
(2)如果2i>n则结点i无左孩子,否则其左孩子是结点2i
(3)如果2i+1>n则结点i无右孩子,否则其右孩子是结点2i+1
1.1.2 二叉树的2种存储结构
1.1.2.1树的顺序存储结构
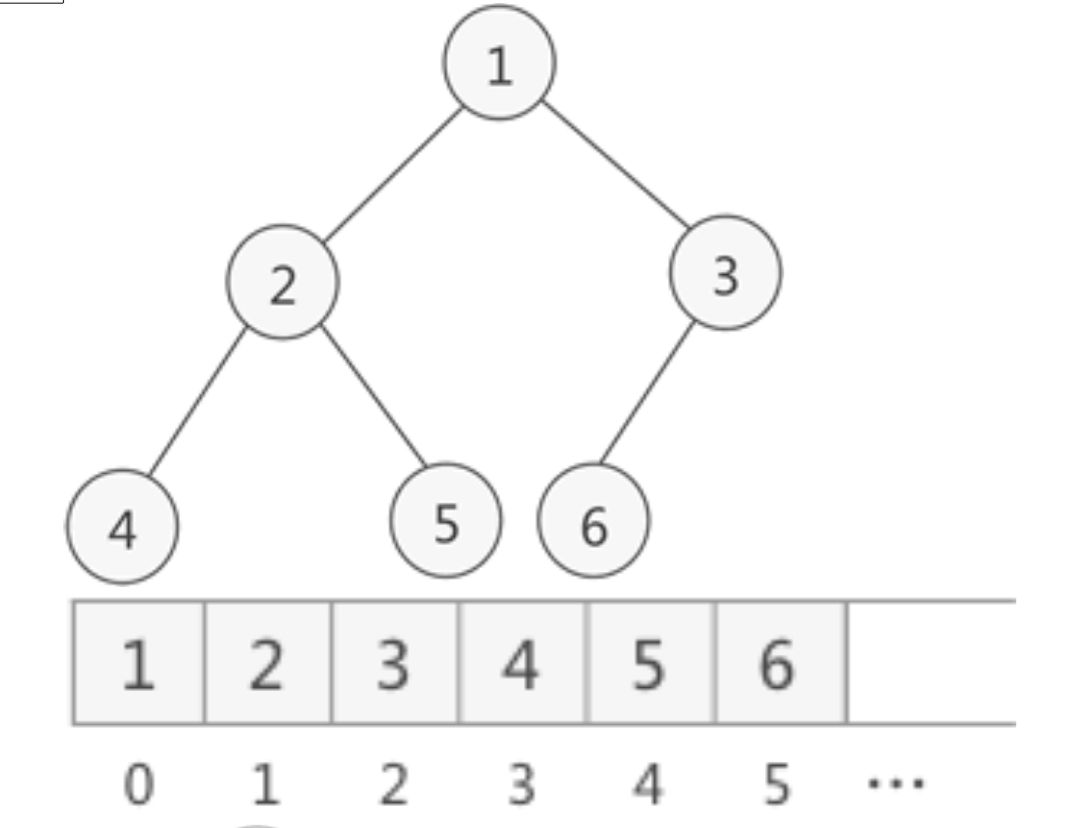
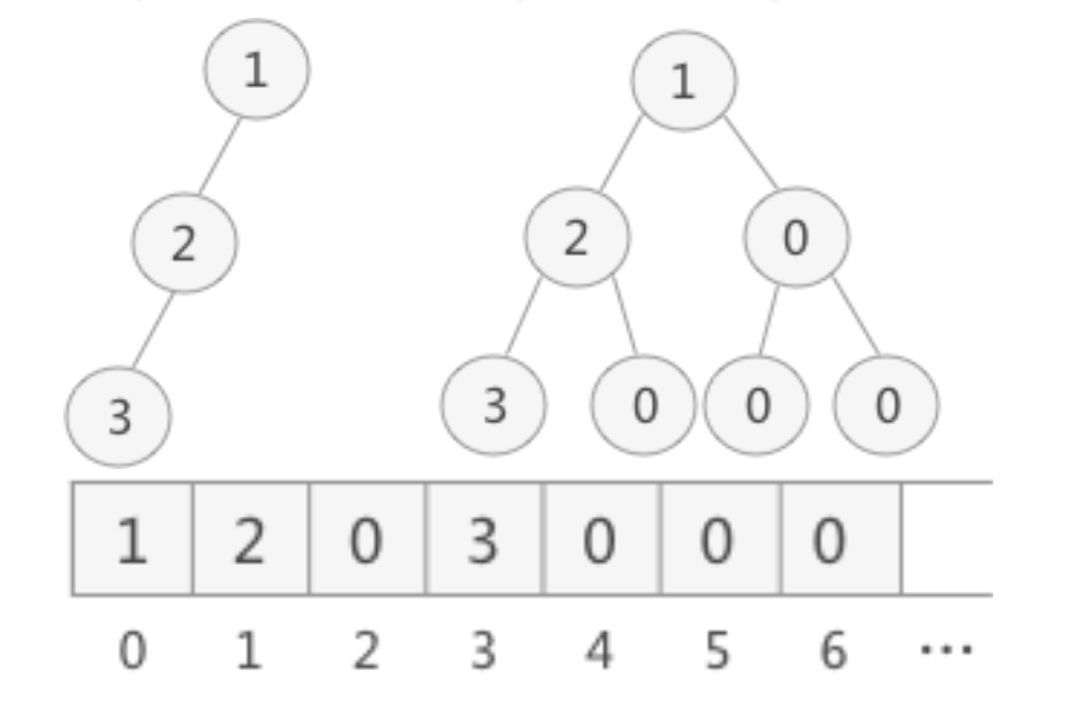
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等
- 完全二叉树
对一颗具有n个结点的二叉树按层序遍历,如果编号i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这颗二叉树称为完全二叉树
- 满二叉树
在一颗二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树
- 普通二叉树
由于二叉树一般是不完美的,所以会对存储空间造成严重浪费,一般情况顺序存储结构只适用于完全二叉树
1.1.2.2树的链式存储结构
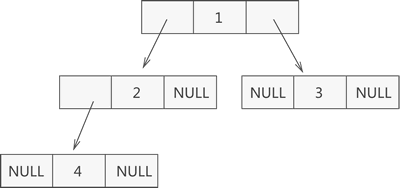
既然顺序存储适用性不强,我们就要考虑链式存储结构。二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。

指向左孩子结点的指针(Lchild);结点存储的数据(data);指向右孩子结点的指针(Rchild);
- 结构定义
//二叉树的链表结构
typedef char ElementType;/* 所有ElementType等同于char */
typedef TNode* Position;
typedef Position BinTree;/* 二叉树类型 */
struct TNode {
ElementType Data; /* 结点数据 */
BinTree Left; /* 指向左子树 */
BinTree Right; /* 指向右子树 */
};
1.1.3 二叉树的构造
- 先序遍历建二叉树
/* 按前序输入二叉树中结点的值(一个字符) */
/* #表示空树,构造二叉链表表示二叉树T */
void CreateBiTree(BiTree* T)
{
TElemType ch;
scanf("%c", &ch);
ch = str[index++];
if (ch == '#')
*T = NULL;
else
{
*T = (BiTree)malloc(sizeof(BiTNode)); /* 生成根结点 */
if (!*T)
exit(OVERFLOW);
(*T)->data = ch;
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
}
1.1.4 二叉树的遍历
- 二叉树的前序遍历
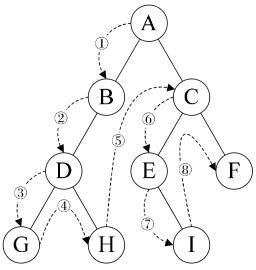
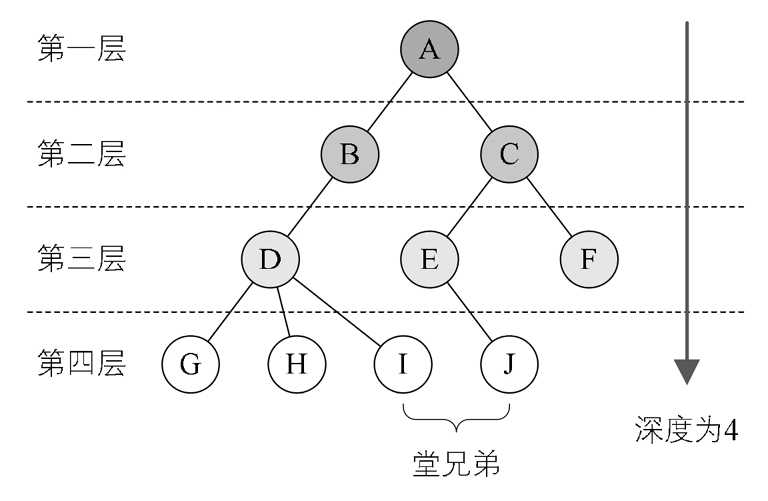
前序遍历:若根节点不为空,则先访问根节点,然后先序遍历左子树,最后先序遍历右子树;如下图所示,遍历的顺序为ABDGHCEIF
1)算法的递归定义是:
若二叉树为空,则遍历结束;否则
⑴ 访问根结点;
⑵ 先序遍历左子树(递归调用本算法);
⑶ 先序遍历右子树(递归调用本算法)。
2)代码实现:
void PreorderTraversal(BinTree BT)
{
if (BT) {
//根->左->右
printf("%d ", BT->Data);
PreorderTraversal(BT->Left);
PreorderTraversal(BT->Right);
}
}
- 二叉树的中序遍历
中序遍历:若根节点不为空,则先中序遍历左子树,再访问根节点,最后中序遍历右子树;如下图所示,遍历的顺序为GDHBAEICF
1)算法的递归定义是:
若二叉树为空,则遍历结束;否则
⑴ 中序遍历左子树(递归调用本算法);
⑵ 访问根结点;
⑶ 中序遍历右子树(递归调用本算法)。
2)代码实现:
void InorderTraversal(BinTree BT)
{
if (BT) {
//左->根->右
InorderTraversal(BT->Left);
printf("%d ", BT->data);
InorderTraversal(BT->Right);
}
}
- 二叉树的后序遍历
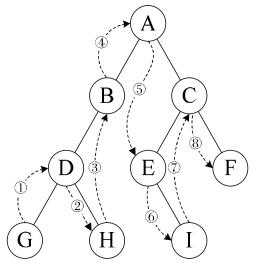
后序遍历:若根节点不为空,则首先后序遍历左子树,其次后序遍历右子树,最后访问根节点;如下图所示,遍历的顺序为GHDBIEFCA
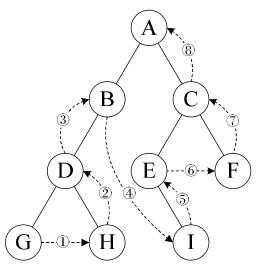
- 递归算法:
若二叉树为空,则遍历结束;否则
⑴ 后序遍历左子树(递归调用本算法);
⑵ 后序遍历右子树(递归调用本算法);
⑶ 访问根结点。 - 代码实现:
void PostorderTraversal(BinTree BT)
{
if (BT) {
//左->右->根
PostorderTraversal(BT->Left);
PostorderTraversal(BT->Right);
printf("%d ", BT->Data);
}
}
- 二叉树的层序遍历
层序遍历:从上到下,从左到右,依次输出结点数据
- 遍历思路:
定义一个队列queue,从二叉树的根结点开始,依次将每一层指向结点的指针入队。然后将队头元素出队,并输出该指针指向的结点值,如果该结点的左、右孩子不空,则将左右孩子结点的指针入队。重复执行以上操作,直到队空为止。最后得到的序列就是二叉树的层次输出序列。 - 代码实现:
void LevelorderTraversal(BinTree BT)
{
if (BT == NULL)
return;
/*层次遍历需要利用栈结构*/
queue<BinTree>Que;
BinTree front;//遍历二叉树
Que.push(BT);//根结点进栈
while (!Que.empty())//若队列不为空
{
front = Que.front();//第一个元素出栈
Que.pop();
printf("%c", front->data);
if (front->lchild != NULL)//若出栈元素有左右子结点,进栈
Que.push(front->lchild);
if (front->rchild != NULL)
Que.push(front->rchild);
}
}
1.1.5 线索二叉树
将二叉树线索化的二叉树称为线索二叉树,指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树就称为线索二叉树
PS:对二叉树以某种次序遍历使其变为线索二叉树的过程称做是线索化
-
性质
在决定lchild是指向左孩子还是前驱,rchild是指向右孩子还是后继上是需要一个区分标志的,因此我们在每个结点再增设两个标志域ltag和rtag,注意ltag和rtag只是存放0或1数字的布尔型变量。
1)若结点有左子树,则lchild指向其左孩子,ltag为0;否则, lchild指向其直接前驱,ltag为1;
2)若结点有右子树,则rchild指向其右孩子,rtag为0;否则, rchild指向其直接后继,rtag为1 。 -
结点结构如下:
| 左孩子域 | 左孩子标志域 | 结点数据 | 右孩子标志域 | 右孩子域 |
|---|---|---|---|---|
| lchild | ltag | data | rtag | rchild |
- 线索二叉树结构的实现
/* 二叉树的二叉线索存储结构定义 */
typedef char TElemType;
typedef struct BiThrNode /* 二叉线索存储结点结构 */
{
TElemType data; /* 结点数据 */
struct BiThrNode* lchild, * rchild; /* 左右孩子指针 */
int ltag, rtag; /* 左右标志 */
}BiThrNode,* BiThrTree;
- 中序遍历线索化代码
BiThrTree pre; /* 全局变量,始终指向刚刚访问过的结点 */
/* 中序遍历进行中序线索化 */
void InThreading(BiThrTree p)
{
if (p)
{
InThreading(p->lchild);/*递归左子树线索化*/
if (!p->lchild) /* 没有左孩子 */
{
p->ltag = 1; /* 前驱线索 */
p->lchild = pre; /* 左孩子指针指向前驱 */
}
if (!pre->rchild) /* 前驱没有右孩子 */
{
pre->rtag = 1; /* 后继线索 */
pre->rchild = p; /* 前驱右孩子指针指向后继 */
}
pre = p; /* 保持pre指向p的前驱 */
InThreading(p->rchild);/*递归右子树线索化*/
}
}
-
中序线索二叉树特点?
中序线索化代码和中序遍历代码几乎完全一样,只不过将本是打印结点的功能改成了线索化的功能 -
遍历线索二叉树
/* T指向头结点,头结点左链lchild指向根结点,头结点右链rchild指向中序遍历的 */
/* 最后一个结点。中序遍历二叉线索链表表示的二叉树T */
Status InOrderTraverse_Thr(BiThrTree T)
{
BiThrTree p;
p = T->lchild; /* p指向根结点 */
while (p != T) /* 空树或遍历结束时,p==T */
{
while (p->LTag == 0)/* 当LTag==0时循环到中序序列第一个结点 */
p = p->lchild;
printf("%c", p->data);
while (p->RTag == 1 && p->rchild != T)
{
p = p->rchild;
printf("%c", p->data); /* 访问后继结点 */
}
p = p->rchild; /* p进至其右子树根 */
}
return OK;
}
1.1.6 二叉树的应用--表达式树
思路:
1.定义两个栈,分别是存放操作数和运算符,遍历字符串,如果是操作数就入栈,如果是运算符,判断栈顶与此时遍历运算符的优先级关系
(1)若栈顶元素小,则入栈
(2)若相等,则出栈
(3)若栈顶元素大,则取出两操作数和运算符栈顶元素建树,注意建好子树后要将根节点入操作数栈
2.字符串遍历完后,反复取出两操作数和运算符栈顶元素建树,建好子树后要将根节点入操作数栈,直到运算符栈空为止,就这样一步一步从叶子建树,一直建到最上方的根结点.建好的二叉树如下
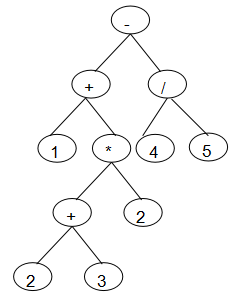
叶子结点均为操作数,非叶子结点均为运算符
3.建好表达式树后,就开始计算,采用后序遍历递归计算,将每一次的计算结果返回,一直到根节点结束,此时的结果就是表达式结果
伪代码:
void InitExpTree(BTree& T, string str)//建表达式的二叉树
{
while (遍历字符串)
{
如果是操作数
生成树结点
结点的左右孩子都置为空
入操作数栈
否则为运算符
栈顶元素与字符串进行符号比较优先级
<://入运算符栈
op.push(str[i]); break;
=://出运算符栈
op.pop(); break;
>://申请空间赋值data结点,使右子树为栈顶数字并将随后的栈顶数字赋值给左子树
新生成树结点
运算符栈顶出栈作为树结点
操作数两个出栈分别作为树结点的左右孩子
再把根结点入操作符栈
break;
}
while (op.top() != '#')//直到运算符栈空
{
新生成树结点
运算符栈顶出栈作为树结点
操作数两个出栈分别作为树结点的左右孩子
再把根结点入操作符栈
}
}
double EvaluateExTree(BTree T)//计算二叉树
{
if (遍历二叉树)//树不空
{
if (T的左右孩子都空,返回结果)//
return 根节点数据;
//后序遍历计算:左右根
num1 = EvaluateExTree(T->lchild);
num2 = EvaluateExTree(T->rchild);
switch (T->data)
case'+':
return num1 + num2;break;
case'-':
return num1 - num2;break;
case'*':
return num1 * num2;break;
case'/':
if (分母==0)
cout << "divide 0 error!";exit(0);
return num1 / num2; break;
}
}
1.2 多叉树结构
树是n个结点的有限集。n=0时称为空树。在任意一颗非空树中:
①有且仅有一个特定的称为根的结点;
②当n>1时,其余结点可分为m个互不相交的有限集T1、T2、···、Tm,其中每一个集合本身又是一棵树,并且称为根的子树
- 树的基本术语
-
不同的节点:根节点、内部节点、叶子节点以及节点的度
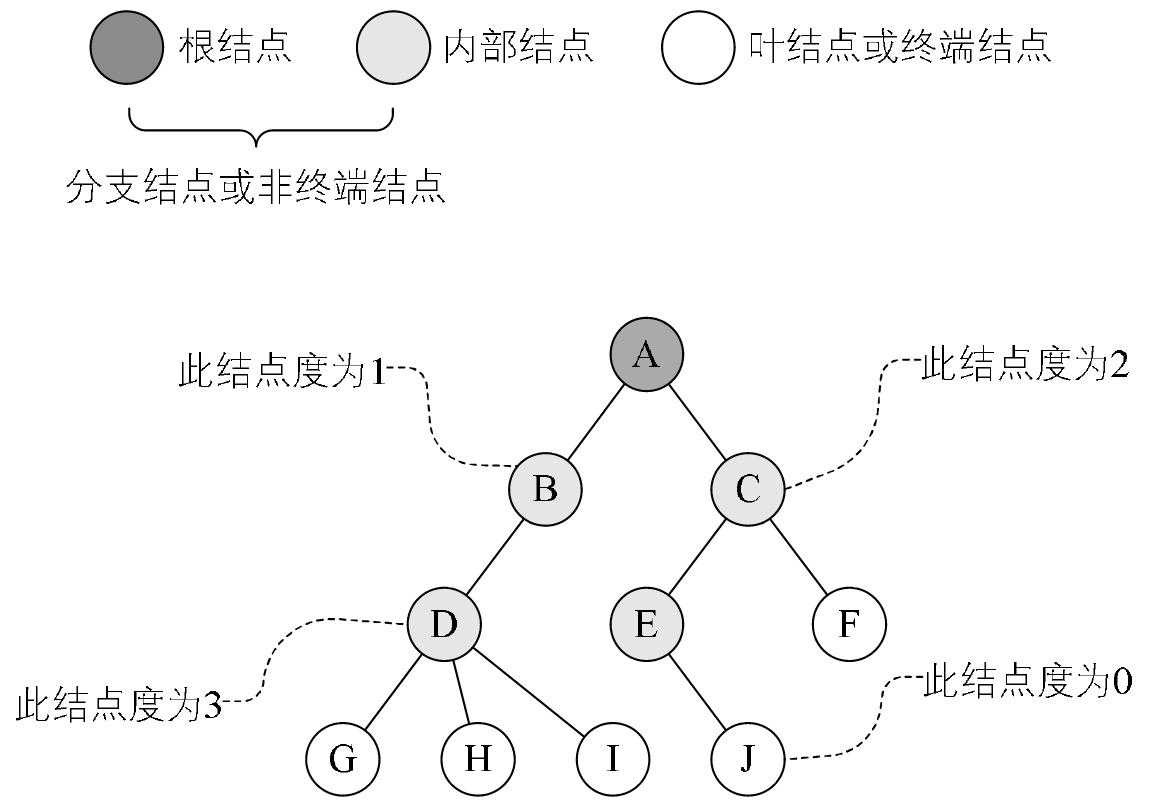
-
节点的关系:双亲与孩子
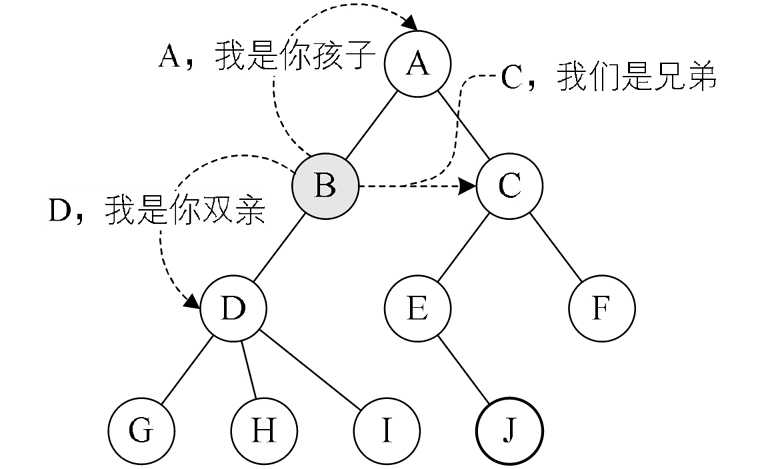
-
节点的层次:结点的层次(Level)从根开始定义起,根为第一层,根的孩子为第二层。树中结点的最大层次称为树的深度(Depth)或高度。
1.2.1 多叉树结构
- 双亲表示法
/* 树的双亲表示法结点结构定义 */
typedef int TElemType;
typedef struct PTNode /*结点结构*/
{
TElemType data; /*结点数据*/
int parent; /*双亲位置*/
}PTNode;
typedef struct /*树结构*/
{
PTNode nodes[10]; /*结点数组*/
int r, n; /*根的位置和结点数*/
}PTree;
- 孩子表示法
/* 树的孩子表示法结构定义 */
typedef int TElemType;
typedef struct CTNode /*孩子结点*/
{
struct CTNode* next; /*结点数据*/
int child; /*孩子位置*/
}CTNode;
typedef struct /*表头结构*/
{
TElemType data;
ChildPtr firstchild;
}CTBox;
typedef struct /*树结构*/
{
CTBox nodes[10]; /*结点数组*/
int r, n; /*根的位置和结点数*/
}CTree;
- 儿子兄弟表示法
任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,设置两个指针分别指向该结点的第一个孩子和此结点的右兄弟
/*树的儿子兄弟表示法结构定义*/
typedef struct CSNode
{
TElemType data;
struct CSNode* firstchild, * rightsib;
}CSNode,*CSTree;
| 结点数据 | 第一个孩子 | 右兄弟 |
|---|---|---|
| data | firstchild | rightsib |
1.2.2 多叉树的先序遍历
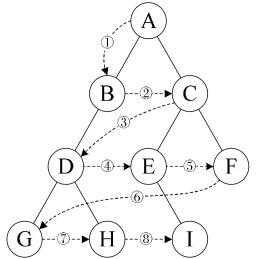
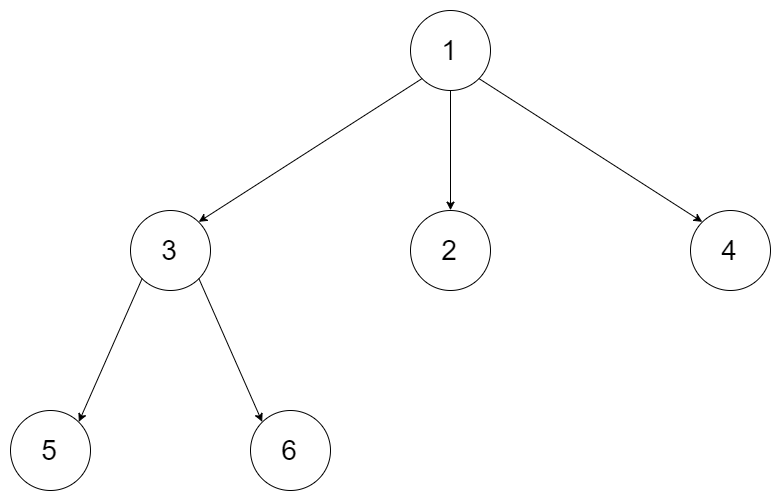
树的先序遍历通俗讲就是按照“根左右”的顺序。如下图所示,遍历结果是:[1,3,5,6,2,4]
1.3 哈夫曼树
哈夫曼树相关的几个名词
-
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。图 1 中,从根结点到结点a之间的通路就是一条路径。
-
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为i-1。图 1 中从根结点到结点c的路径长度为 3。
-
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,图 1 中结点 a 的权为 7,结点 b 的权为 5。
-
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。
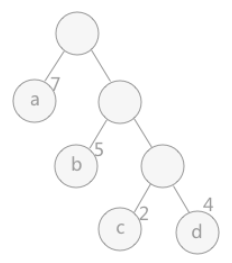
图1 哈夫曼树
1.3.1 哈夫曼树的概念
(1)简单路径长度
所谓树的简单路径长度,是指从树的跟节点到每个节点的路径长度之和。
完全二叉树是简单路径长度最小的二叉树。
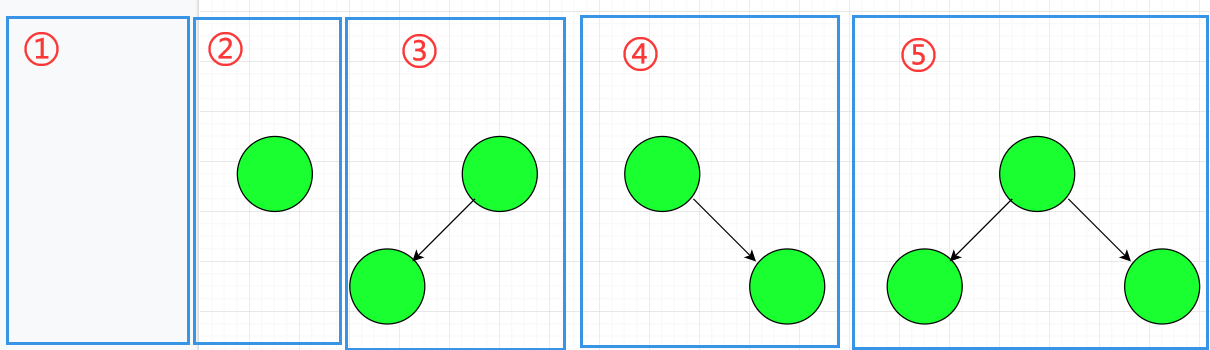
(2)加权路径长度
所谓树的加权路径长度,是指树中所以带权(非0)叶节点的加权路径长度之和。
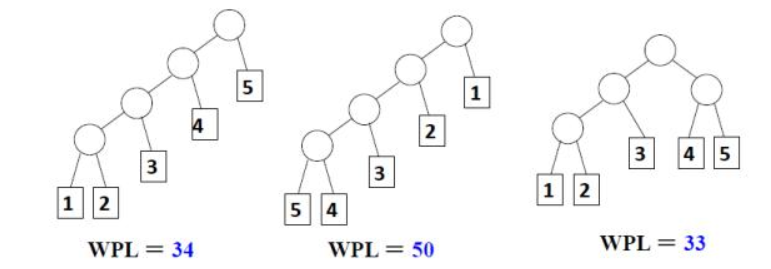
如下图所示,不同的树结构,加权路径长度也不一样。
(3)哈夫曼树的定义
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”。
原则:在构建哈弗曼树时,要使树的带权路径长度最小,所以权重越大的结点离树根越近。
(4)哈夫曼树能解决什么问题?
- 远距离通信的数据传输的最优化问题————哈夫曼编码
- 判定树————分数等级转换
1.3.2 哈夫曼树的结构体
//哈夫曼树的结点类型
typedef struct HTreeNode
{
char data[5]; //每个结点是字符类型,最多5个字符
int weight; //字符所占的权重
int parent; //双亲结点所在下标
int left; //左孩子结点所在下标
int right; //右孩子结点所在下标
}HTNode;
1.3.3 哈夫曼树构建
哈夫曼树的构造过程需要借助最小堆算法。
①首先将原始数据构造出一个最小堆
②然后每次从堆中选取值最小两个节点,计算他们的权重之和,作为一个新节点的值
③然后插入到最小堆中,直到所有数据节点都构造完毕,成为一个最大堆。
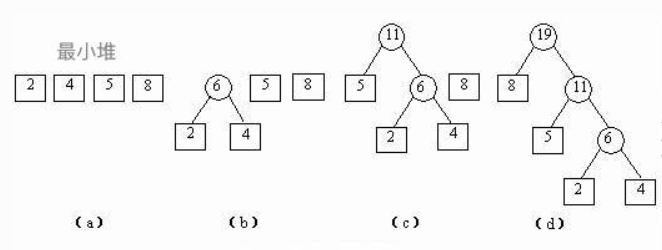
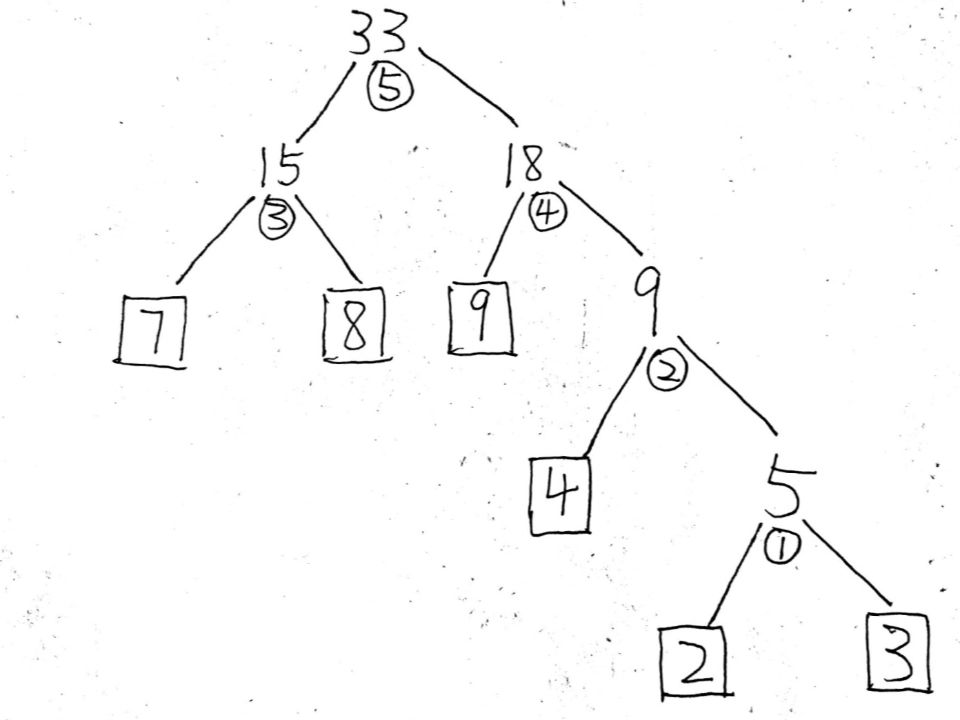
- 例如:2,3,4,7,8,9这组叶子结点
① 2,3,4,7,8,9中2和3最小,权重和为5
② 4,5,7,8,9中4和5最小,权重和为9
③ 7,8,9,9中7和8最小,权重和为15
④ 9,9,15中9和9最小,权重和为18
⑤ 剩下15,18,权重和为33
1.3.4 哈夫曼树编码
哈夫曼编码是一种编码方式,是一种用于无损数据压缩的权编码算法。编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。
① 在数字通信中,经常需要将传送的文字转换成由二进制字符0、1组成的二进制串,这一过程被称为编码。在传送电文时,总是希望电文代码尽可能短,采用哈夫曼编码构造的电文的总长最短。
② 由常识可知,电文中每个字符出现的概率是不同的。假定在一份电文中,A,B,C,D四种字符出现的概率是4/10,1/10,3/10,2/10,若采用不等长编码,让出现频率低的字符具有较长的编码,这样就有可能缩短传送电文的总长度。
③ 采用不等长编码时要避免译码的二义性和多义性。假设用0表示C,用01表示D,则当接收到编码串01,并译码到0时,是立即译出C,还是接着下一个字符1一起译为对应的字符D,这样就产生了二义性。 因此,若对某一字符集进行不等长编码,则要求字符集中任一字符的编码都不能是其他字符编码的前缀,符合此要求的编码叫做前缀编码。
④ 为了使不等长编码也是前缀编码,可以用字符集中的每个字符作为叶子结点生成一棵编码二叉树,为了获得最短的电文长度,可将每个字符出现的频率作为字符的权值赋予对应的叶子结点,求出此树的最小带权路径长度就是电文的最短编码。
⑤ 可以根据哈夫曼算法构造哈夫曼树T。设需要编码的上述电文字符集d={A,B,C,D},在电文中出现的频率集合p={4/10,1/10,3/10,2/10}
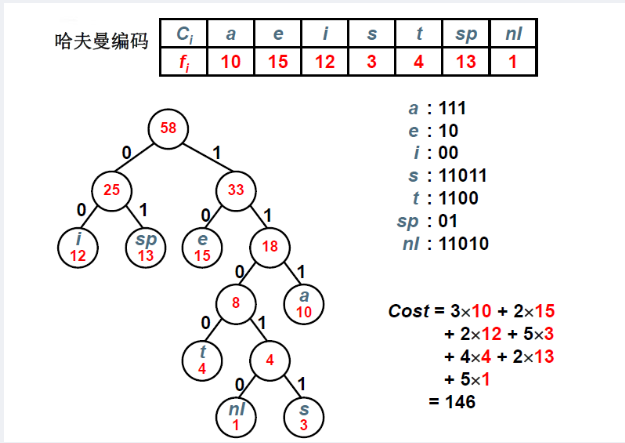
我们以字符集中的字符作为叶子结点、频率作为权值,构造一棵哈夫曼树。
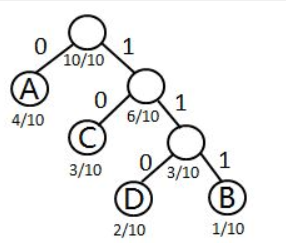
其中,每个结点分别对应一个字符,对T中的边做标记,把左分支记为“0”,右分支标记为“1”。定义字符的编码是从根结点到该字符所对应的叶子结点的路径上,各条边上的标记所组成的序列就是哈夫曼编码。
---- A的编码:0,C的编码:10,D的编码:110,B的编码:111.
1.4 并查集
- 什么是并查集?
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
- 并查集解决什么问题?
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。
首先在地图上给你若干个城镇,这些城镇都可以看作点,然后告诉你哪些对城镇之间是有道路直接相连的。最后要解决的是整幅图的连通性问题。比如随意给你两个点,让你判断它们是否连通,或者问你整幅图一共有几个连通分支,也就是被分成了几个互相独立的块。像盆友圈这题,问最大朋友圈的人数,实际上就是并查集的合并,把每个俱乐部看成一个集合,然后对这些集合进行合并。
- 优势在哪里?
并查集在解决连通性问题上有很大优势,比如检查地图上两点是否连通,用并查集可以大大提高查找效率
1.5 谈谈你对树的认识及学习体会
之前听说数据结构有.搞脑子,如今看来确实如此,在数据结构中有四个重要的结构分别是线性表,栈与队列,树,图。在树结构的学习中明显感到了树的复杂性和变化丰富度,树有非常多的应用————目录树、HTML、公司上下级关系、最短路径、线路规划问题。。。由此可见树这货还是很有用的,当然啦,也并不是说线性表就没有用,因为不同的结构处理的问题是不太一样的,我们应用不同的结构处理问题就是为了提高算法的效率,能高效解决问题的东西都是好东西!希望学习数据结构能让我的代码跑得更快一些。
2.PTA实验作业
2.1 jmu-ds-输出二叉树每层节点
2.1.1 解题思路及伪代码
- 解题思路
- 先序遍历递归创建二叉树
- 利用栈结构层序遍历输出结点
- 该题还要考虑结点的高度,故设立两个结点bt和eb,bt结点用来层序遍历,eb结点用来保存每层最右结点,
若bt遍历到eb时,说明要开始遍历下一层了
- 伪代码
void LevelOrder(BTree bt)
{
int h = 0, flag = 0;
BTree eb;
eb = bt;
queue<BTree>q;
if (空树)
退出
根结点入队
while (栈不为空)
if (队头 == 该层最右结点)
h++; //换行输出
打印行数
eb保存该层最右结点
bt保存队头结点
打印bt结点数据
if (bt有左孩子) 入队
if (bt有右孩子) 入队
队头bt出队
}
2.1.2 总结解题所用的知识点
- 先序遍历建立二叉树
- 二叉树的层序遍历,和其他遍历不同之处是利用了栈结构
- 这题还要求输出结点的高度,巧妙的设计了一个结点用来保存最右结点,解决了高度问题
2.2 目录树
2.2.1 解题思路及伪代码
- 解题思路
- 首先根据输入 建立二叉树
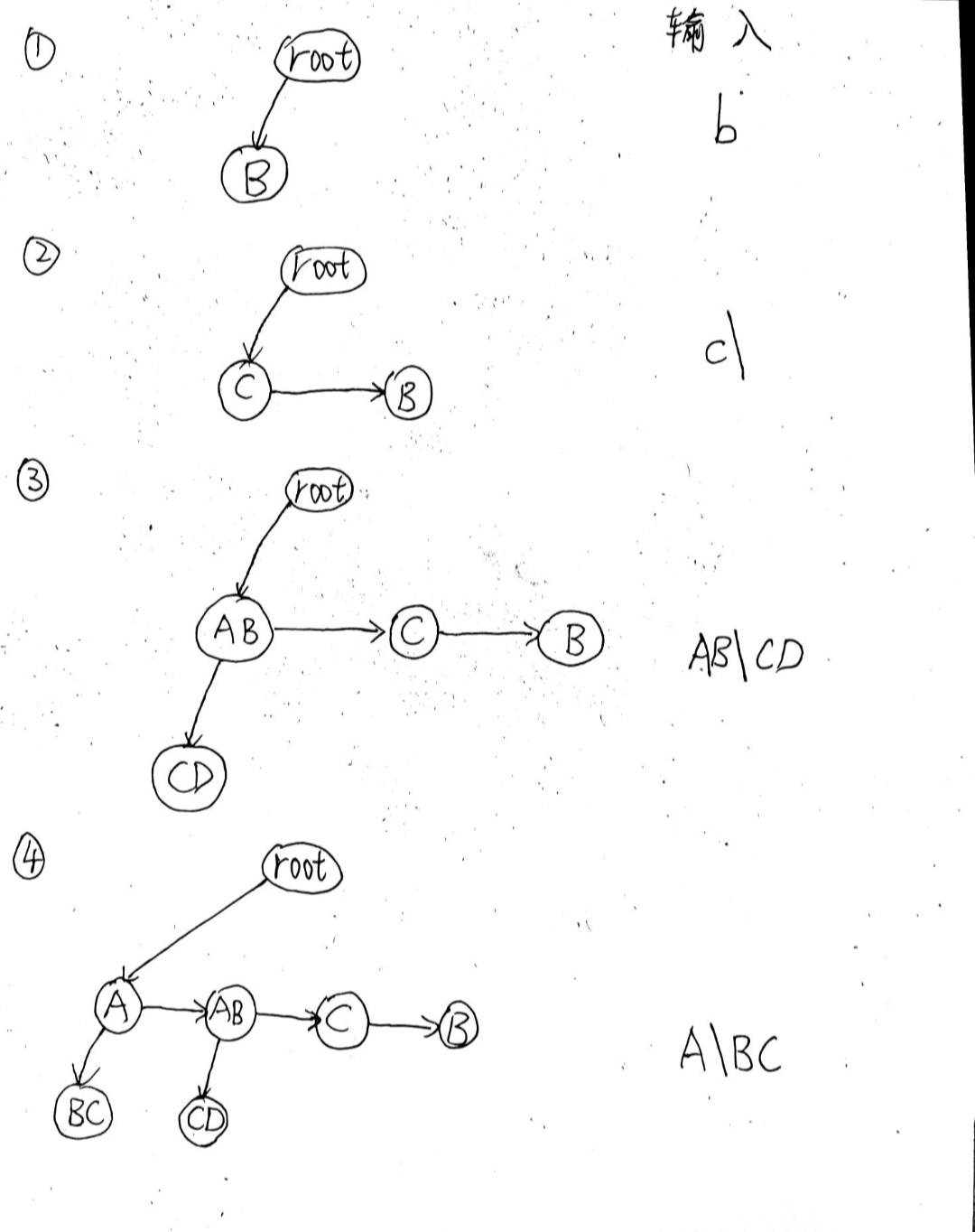
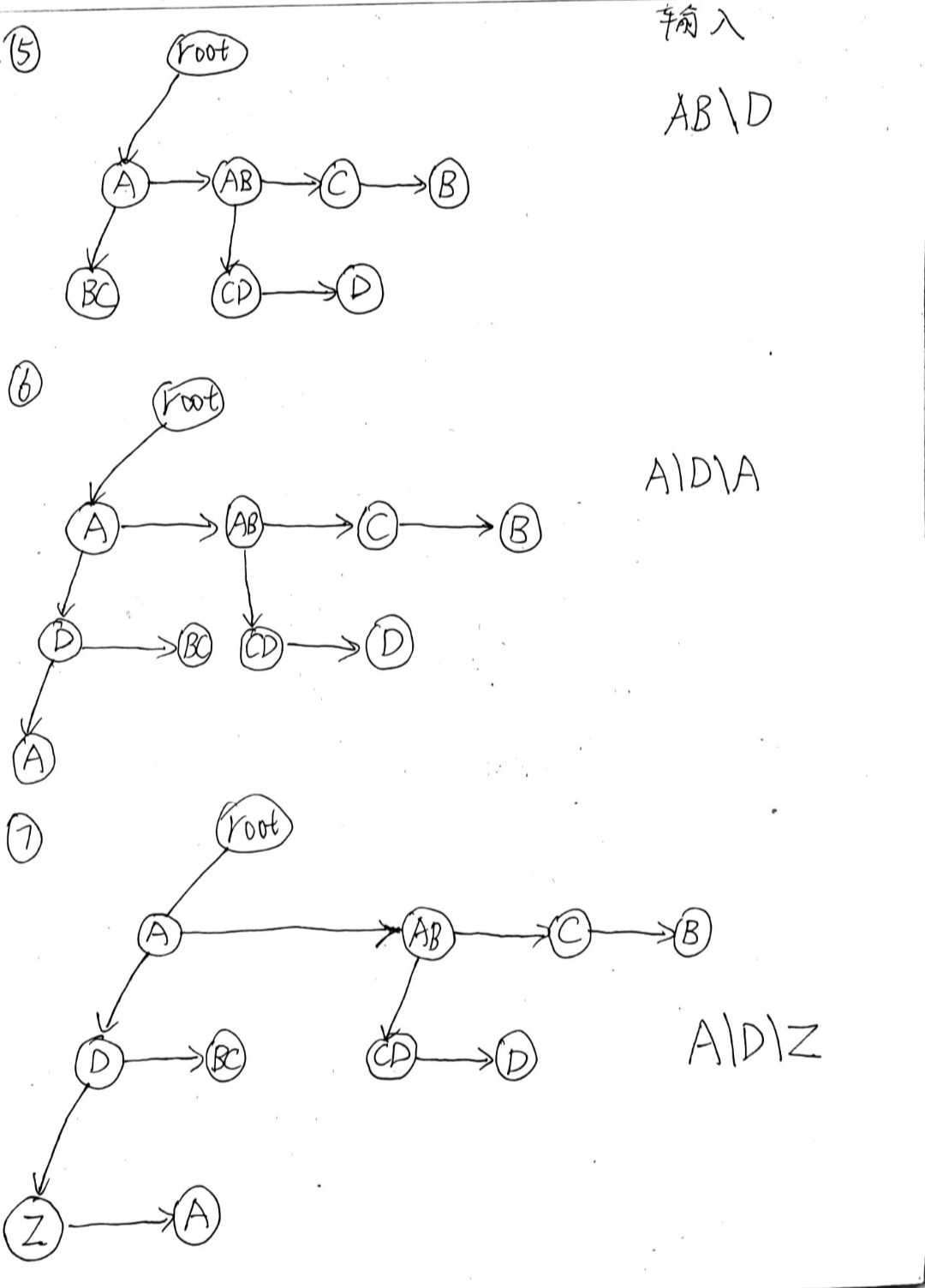
- 整理成二叉树的形式
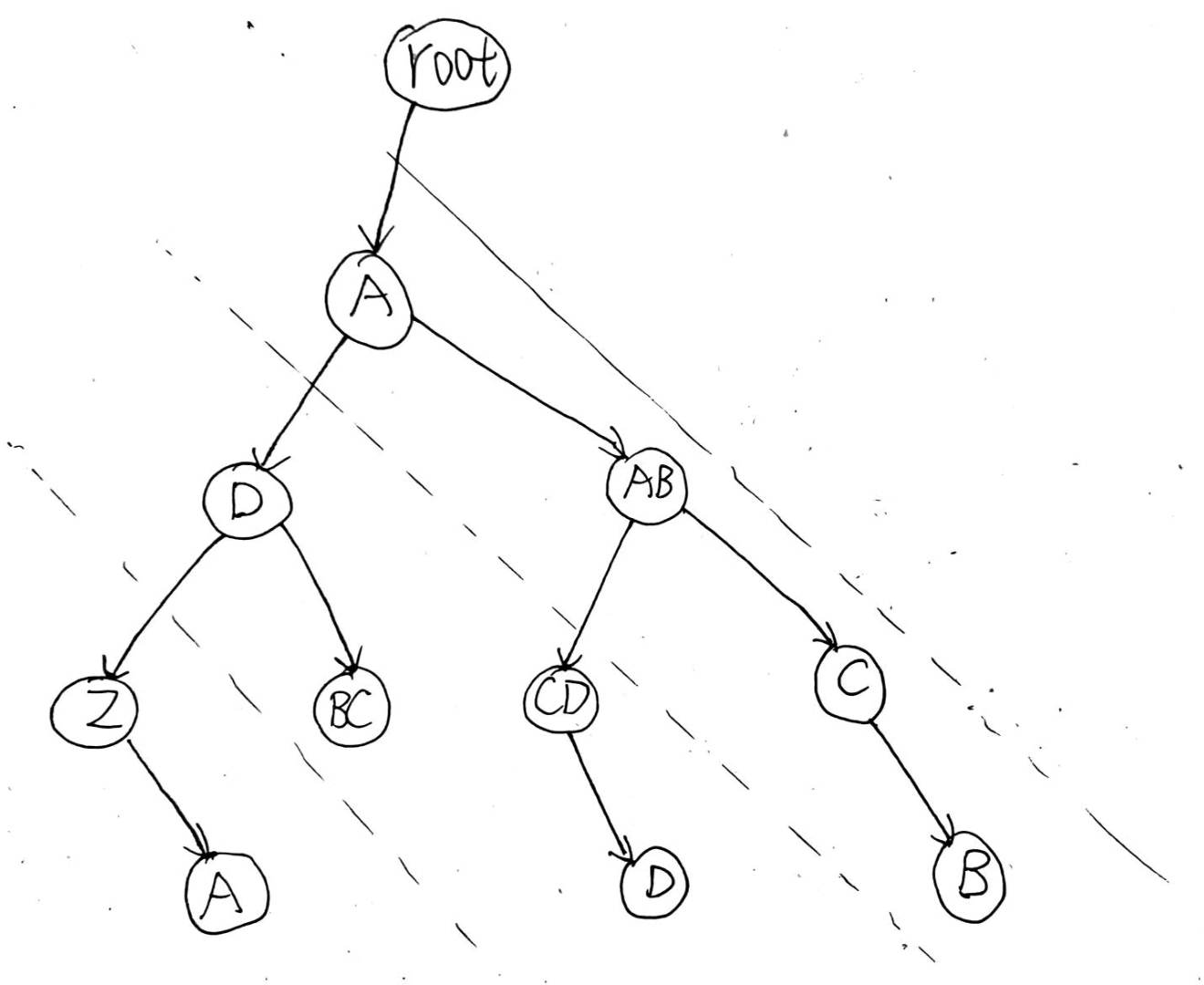
- 我们对这棵树进行先序遍历,得到的结果和输出结果完全一致,我们只需要在前序遍历的基础上控制空格输出即可,那么如何控制空格输出呢?由于我们是用孩子兄弟表示法,左子树是孩子要加俩空格,右子树是兄弟,不用加空格,这样就可以解决空格的问题了
- 分割字符串伪代码
void createTree(CSTree pre, string str)
{
getline(cin, str);
for (int i = 0; i < str.size(); i++)
{
if (str[i]为'\')
复制下标idx到i的字符串file;
idx移动到i之后的下一个字符串;
输出file;
}
if (字符串末尾字符串表示文件)
复制下标idx到i的字符串file;
输出file
}
- 打印目录树伪代码
CSTree insertNode(CSTree t, string str, int flag)
{
if (所在目录没孩子)
设置所在目录的孩子结点为新结点
return;
else //查找插入位置
查找正确的插入位置;
if (找不到插入位置)
插在目录兄弟链的表尾;
else if (目录或文件已经存在)
return; //不需要插入
else //通常情况
在对应位置插入结点;
return;
}
2.2.2 总结解题所用的知识点
- 利用孩子兄弟链结构进行存储,查找某个结点的某个孩子比较方便
- 前序递归遍历,输出结点,这题还要控制空格输出
3.阅读代码
3.1 题目及解题代码
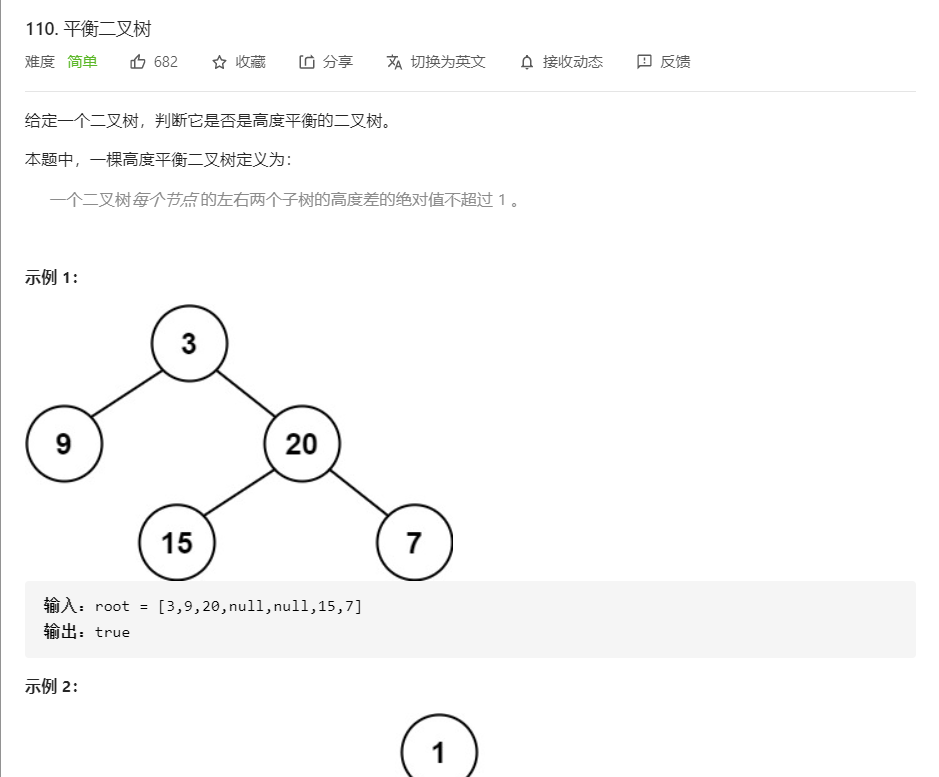
int height(struct TreeNode* root) {
if (root == NULL) {
return 0;
} else {
return fmax(height(root->left), height(root->right)) + 1;
}
}
bool isBalanced(struct TreeNode* root) {
if (root == NULL) {
return true;
} else {
return fabs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/balanced-binary-tree/solution/ping-heng-er-cha-shu-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.2 题目所需知识点
前言
平衡二叉树是二叉排序树的改进版
也就是说平衡二叉树是二叉排序树的一个特殊情况
二叉排序树的定义
或者是空树
或者是满足以下性质的二叉树
★若它的左子树不空,则左子树上的所有关键字的值均小于根关键字的值
★若它的右子树不空,则右子树上的所有关键字的值均大于根关键字的值
平均查找长度ASL
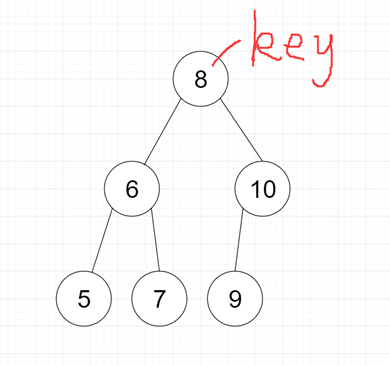
二叉搜索树一定程度上可以提高搜索效率,但是当原序列有序时,例如序列 A = {5,4,3,2,1},构造二叉搜索树下图,依据此序列构造的二叉搜索树为左斜树。
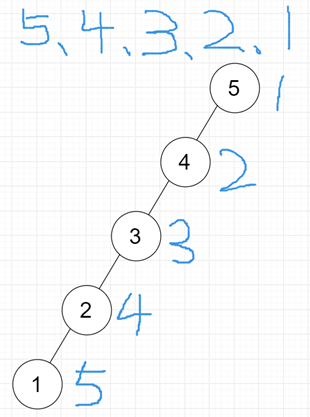
ASL=(1+2+3+4+5)/5=3
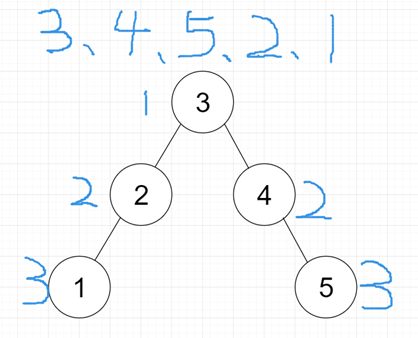
ASL=(1+2+2+3+3)/5=2.2
平均查找长度越小,查找速度越快,所以我们要让这颗二叉树尽可能的矮
平衡因子
左子树高度-右子树高度
平衡二叉树
我们将每个结点的平衡因子的绝对值都不超过1的二叉排序树称为平衡二叉树
3.3 该题的设计思路及伪代码
- 解题思路
这道题中的平衡二叉树的定义是:二叉树的每个节点的左右子树的高度差的绝对值不超过 1,则二叉树是平衡二叉树。根据定义,一棵二叉树是平衡二叉树,当且仅当其所有子树也都是平衡二叉树,因此可以使用递归的方式判断二叉树是不是平衡二叉树.定义函数 height,用于计算二叉树中的任意一个节点 p 的高度,有了计算节点高度的函数,即可判断二叉树是否平衡。具体做法类似于二叉树的前序遍历,即对于当前遍历到的节点,首先计算左右子树的高度,如果左右子树的高度差是否不超过 1,再分别递归地遍历左右子节点,并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。
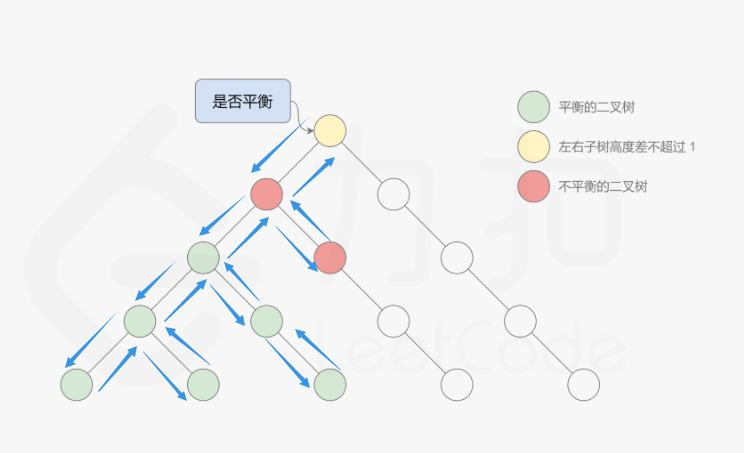
复杂度分析
- 时间复杂度:O(n^2),其中 n 是二叉树中的节点个数。
最坏情况下,二叉树是满二叉树,需要遍历二叉树中的所有节点,时间复杂度是 O(n)。
对于节点 p,如果它的高度是 d,则height(p) 最多会被调用 d 次(即遍历到它的每一个祖先节点时)。对于平均的情况,一棵树的高度 h 满足 O(h)=O(logn),因d<=h,所以总时间复杂度为O(nlogn)。对于最坏的情况,二叉树形成链式结构,高度为O(n),此时总时间复杂度为 O(n^2)。 - 空间复杂度:O(n),其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数,递归调用的层数不会超过 n。
3.4 分析该题目解题优势及难点
该题采用的是自顶向下的递归,这个方法比较容易理解,简单来说就是先序遍历,计算每个结点是否为平衡二叉树,而另一种自底向上的递归方法的时间复杂度为O(n),效率会更高一些。