MOSSE（DSST）类和KCF类中滤波器推导结果不一致的解释

首先要说明，DSST//BMVC2014类的CF是从MOSSE//CVPR2010模型得到的，是从信号的角度考虑问题，该类CF直接认为信号和滤波器之间存在相关的关系

而KCF//TPAMI2015类CF并不默认这一关系，其依然是从传统的分类器（岭回归）角度去求解一个分类器的权重，但是由于其强制训练样本为循环矩阵形式，从而内嵌了权重w有一个类似于相关滤波器的作用。

这两种是不同的，所以最后的检测结果实际上也是有区别的。

而MOSSE（DSST）类的滤波器h和KCF类的权重w实际上有比较大的区别。因为在检测时，在时域上一个是相关运算，另一个是内积运算。明显不同。

 

问题的提出：

  有两个问题：

 问题1: 在DSST和KCF论文最后的推导上，他们的结果是不一样的，DSST是将最后分子中的共轭放在理想输出G上，如上面的公式，而KCF中的共轭是放在特征上的。

DSST:

 

 

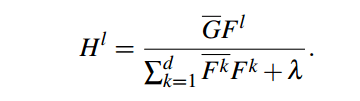
KCF:

                         

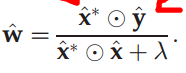
同样的差异也存在于CSR-DCF//CVPR2017，该论文最后的推导依然是把共轭放在输出G上的

 

 

 

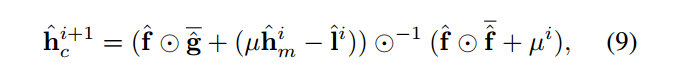
 问题2: 在DSST中的代码处理，却和论文是不一样的，他依然是在特征上取的共轭，而不是在G上取共轭，给人的感觉是DSST的代码实现似乎和KCF论文推导是一致的

 

 

 

问题的解释：

  下面分几点来做该问题解释 

1、公式推导是否正确

（1）MOSSE、DSST等论文的推导结果是没有问题

以DSST为例，推导如下：

这里H是/hat{h}的二维形式，同理F和G也是/hat{f}和/hat{g}的二维形式，都是在频域中的表示。

可以看出和DSST论文的结论一致。

  另外，MOSSE论文中的结论如下：

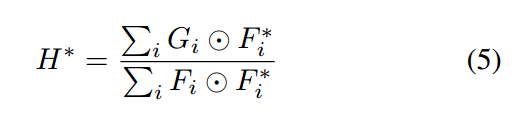
DSST论文中的结论如上文，这两个滤波器，一个表示成H^*,一个表示H，实际上是一回事，都是正确的

（2）KCF公式的推导是有问题，这个已经被讨论过了：

https://zhuanlan.zhihu.com/p/26766703

所以正确的KCF中的权重w（这里不适合在KCF中也把这个叫做滤波器）应该是:

 

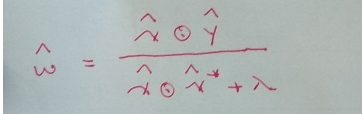
  所以问题1中，DSST和KCF推导之间的差异实际上并不是原问题中共轭是放在特征上还是放在理想输出上的差异

而是MOSSE类的滤波器表示上是有共轭的，而且共轭是放在特征上，而KCF的w则根本就不应该有共轭符号

 

2、两者之间的差异

在MOSSE（DSST）类出现滤波器h的公式表示和KCF的权重w有差异是很正常的。

因为KCF的w并不是滤波器，它和MOSSE类的滤波器h有本质上的区别

在检测实现上，MOSSE是在时域上由滤波器h和检测样本z的相关运算计算得到，即，f(z)=h★z，这里的★表示相关，而在频域上相当于去计算/hat{h}^*/hat{z}。（注意：相关不是卷积，所以转换到频域，相当去前者频域的共轭和后者频域去做元素乘）

而KCF的检测，在时域上由样本z构成的循环矩阵和权重w做乘法计算得到的，即f(z)=Zw,这里循环矩阵的构成形式如KCF论文所示（注意：并不是所有文献对循环矩阵都是按照KCF论文这样按行构成的，诸如CFNET//CVPR2017这样的论文就是按列构成循环矩阵）

综上，这两者出现差异是没有问题的

 

3、DSST论文中的代码实现是否有误

DSST的代码实现是没有问题，分两步讨论：

（1）在滤波器学习上，我们可以看出，其代码实现是这样的

所以，其代码中所学的滤波器，并不是学习了/hat{h},而是学习了/hat{h}^*

（2）在检测上，按照前面的讨论，应该是在频域计算滤波器共轭和样本之间的元素乘。所以DSST的代码实现直接将这里学习的hf（PS.实际上是conj(hf)）去和样本的频域xf做元素乘

所以，代码的实现和论文中公式的推导完全一致，没有问题

 

4、按这两个模型实现的tracker性能是否有差异

按照上面的讨论，MOSSE(DSST)类的滤波器和KCF中的权重根本就不一样，那么最后的检测结果是否一样，换言之，对于一个CF类的tracker，如果我们应用MOSSE模型或者KCF模型去实现tracker的基本核心组件，实验结果上是否一样？

回答是一样的，尽管从出发点上，两者的区别很大，但是归根到最后检测上，即f(z)的表达完全一样（如果不考虑其时态更新方式，详见第6点的讨论），证明如下：

 

首先我们对于DSST和KCF分别计算其f(z)，这里的KCF我们首先以/alpha去计算（P.S.CF论文关于对偶变量/alpha的推导都是正确的）

可以看出两者是完全一样的，另外这里需要说明一点的是，相关运算是不能前后交换的，即h★z≠z★h，不过它们在频域上也就差一个共轭。

所以我们在MOSSE(DSST)类CF是去计算f(z)=h★z还是f(z)=z★h是有区别的。

但是这个在代码实现上是没有差异的，因为代码实现上都是会在response的计算时加一个real。共轭复数的实部是相同的。

 

另外对于KCF，如果我们按照w去推导，也依然能推导出相同的结果

 

5、其他的一些讨论

在其他的一些文献中也有类似的问题，以CVPR2017的oral：CA为例 （这里感谢和@YuKi的交流）

Mueller M, Smith N, Ghanem B. Context-Aware Correlation Filter Tracking// CVPR 2017.

 

该论文在推导实现上都是从KCF模型出发的，但是其代码实现上确实按照MOSSE(DSST)模型去实现的，从上面第4点的讨论，这样的实现是没有问题的。

首先说明CA论文中的推导的错误，在其supplemenary material中，有以下的推导过程：

这里的推导出现了好几处错误，正确的推导如下：

可以看到这里/hat{w}的的形式和KCF中的/hat{w}是完全类似的。

而在其代码实现上（以DCF-CA为例）

滤波器学习：

可以看着这里学习的就是滤波器，而不是像KCF类那样的权重

检测输出：

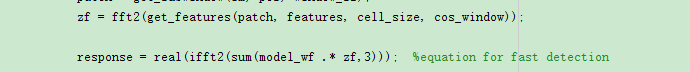
其代码实现和DSST的实现完全一致。

 

6.时态更新方式上的一些讨论

在第4点的讨论上，我们认为KCF和MOSSE的最终实验性能完全一样，是不考虑滤波器的更新的。实际上由于采取了不同的时态更新方式，他们之间还是有细微的区别的

KCF：对alpha和x同时采用时态插值更新

MOSSE：对分子和分母同时采用时态插值更新

CA：对分子和分母相除得到的滤波器采用时态插值更新

 

具体结果如下：

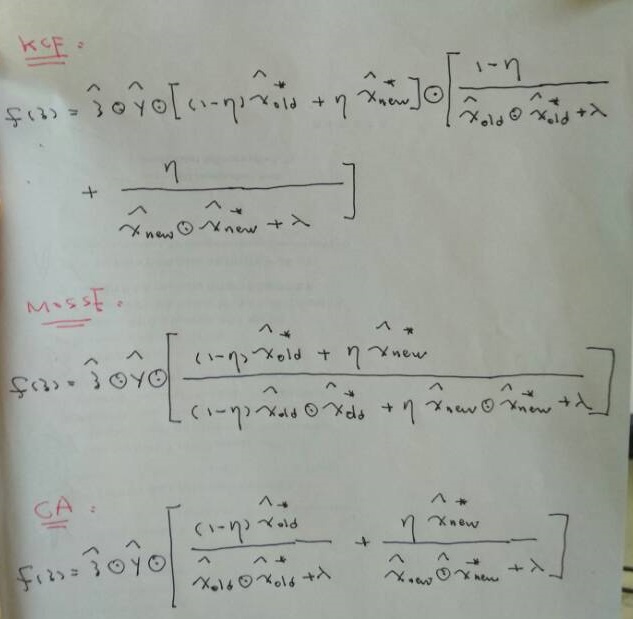
OVER