manacher(马拉车）算法详解

　　manacher算法，用于求字符串中最长回文串。凡是涉及暴力枚举，一般都会超时，尤其当考虑回文串时，必须前后一起判断，复杂度太高。这时，manacher算法在O(n)时间里解决问题。下面看算法。

　　回文子串，正反读都一样，可以看做轴对称的字符串。aba、abba都是。像aba有3个字符，其中心下标是1，记下就行。只是abba包含4个字符，中心是1.5就不好解释了。

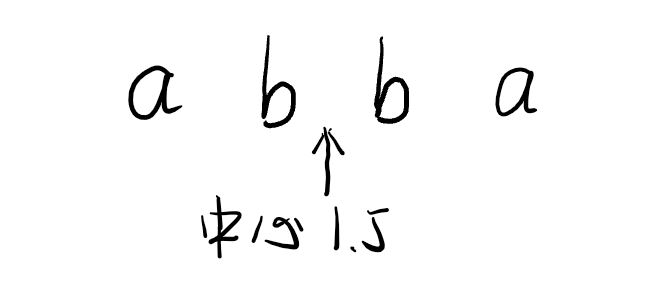
　　于是扩展一下，发现凡是奇数个字符的串，中心可以是int，偶数的话就得是double。怎么办？于是把所有不管什么字符串都强行变成奇数个，方法很简单，只需要在每两个字符中间加一个一样的字符就行。首先，所加的这个字符不能在串中出现，不然求得回文串以后很难区分原字符与新字符。按照网上惯例，加#号。

　　abba变成#a#b#b#a#,有什么用？这个样子中心就落到5上了。只是还有一点，现在#也是字符串的一部分了，所以对于每个#号也要作为中心判断。于是在判断第0位时（最后一位类似）： ch[-1]==ch[1]?r++:continue; 这样就不对了，越界是很严重的问题。于是在这个数组的首尾加上奇特的字符，让判断语句无法通过就行。例如$#a#b#b#a%。为什么前后竟然不一样？首位一致就可能回文了。不过比较好的是，字符串数组末尾会自动添加结束符‘\0’,所以最后一位就不加了。 对于这种DP性质的算法，先假设已经求到一半，再考虑其他剩余部分该怎么通过之前状态得到。在求解过程中，记录以每个字符为中心的回文半径r[]，之前回文串中所达到数组最远的地方f，以及到达f的中心k。举个例子：

 

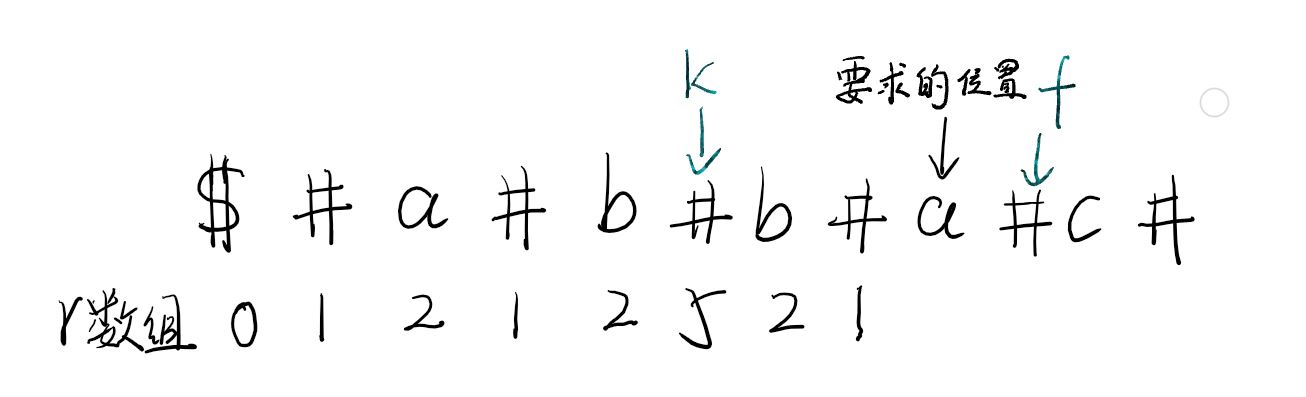
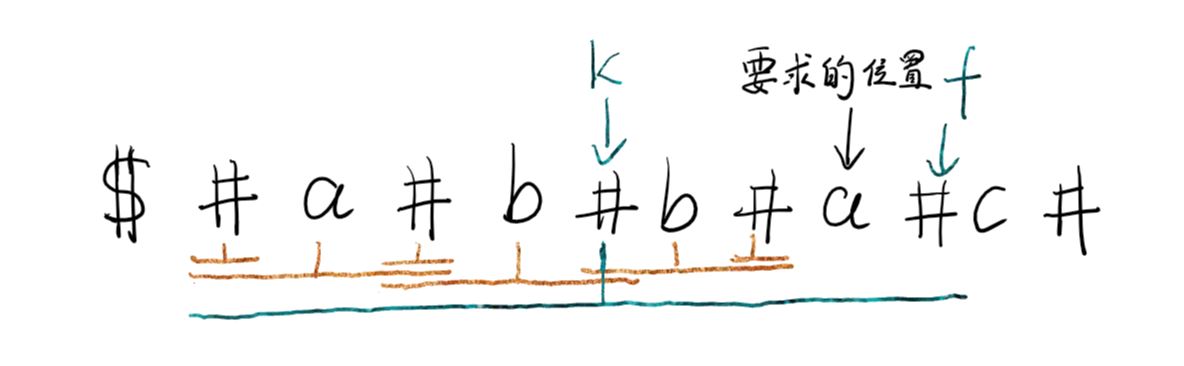
　　 图中下划线为回文子串的范围，可以看到k,f的现实意义。只是k是边界最靠右的子串中心，和最长的没有任何关系。那么求这些东西有什么用？可以看到要求的a(8),在f(9)的左边，也就是在以k为中心的回文串内。既然有DP，那么就要用到之前一部分数据。

　　2,5,8有什么联系吗？在以5为中心的子串中，不但包括了2、5，而且2,5还是对称的。那么3,7对称；1,9对称，321和789就完全相同了。不用从头开始计算，先让r[8]=2，可是即使之前最远的边界，也没有覆盖10，这时候循环判断一下就行。r[10]!=r[6];break;于是r[8]就求完了。

　　不是说DP吗?能否只判断一次就求出答案？这是有条件的。比如要求b(6)，

 

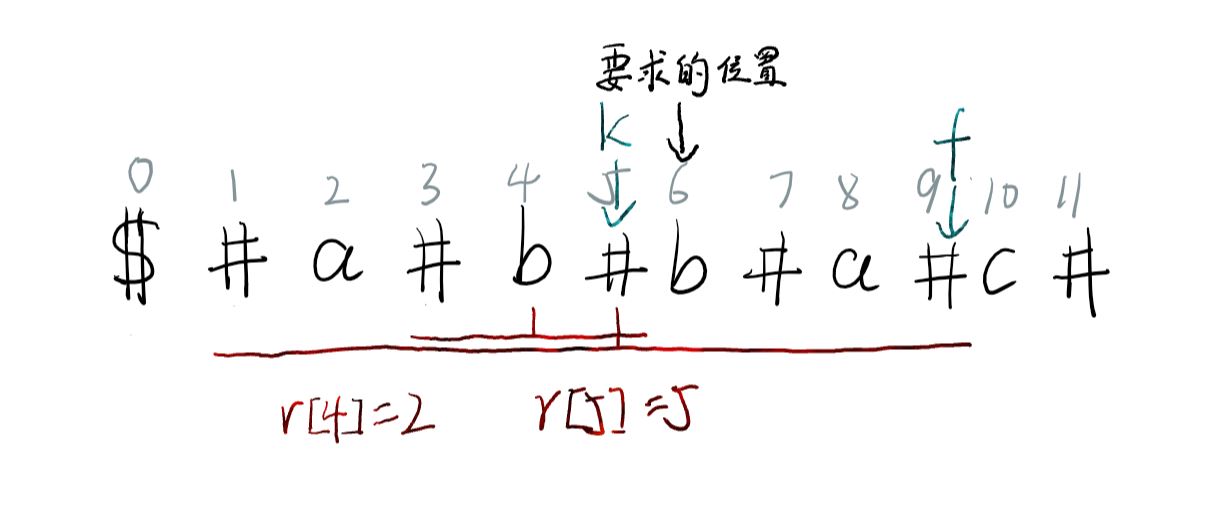
　　可以看到他的另一半b(4)  在串内，就先让r[6]=2。这时，发现89也在求得的串内，也就是和21完全一样。既然以b(4)为中心都不能和2,1变成一家人，b(6)也别想追求8.9了，洗洗睡吧。判断结束，r[6]=2。

　　还有一种情况没说到，就是f在当前判断点左边怎么办？比如求c(10).

　　没人帮你，你就自力更生吧。暴力判断一下就行。结果：ch[8]!=ch[12];r[10]=2.完。

　　manacher算法大致思想就是这样，主要涉及上面3种情况。顺便说一句，在求c(10)的时候，f=10，k=5或者k=10是判断时有没有加‘=’的区别。建议在f相等时保留更长的区间（就是除非f更大，否则k不变），这样可能得到更大的初始值。实际操作时影响应该不大。

附上代码：

void manacher(char *ch)
{
    int len=strlen(ch);
    int k=0,f=0,ans=0;
    for(int i=1;i<=len;i++)
　 {
        if(i<f) r[i]=min(r[(k<<1)-i],f-i);
        else r[i]=1;
        while(ch[i+r[i]]==ch[i-p[i]]) r[i]++;
        if(f<i+r[i]) f=i+r[i],k=i;
        ans=max(ans,r[i]-1);
     }
}