ccf 201609-4 交通规划

 

 

 

 

 

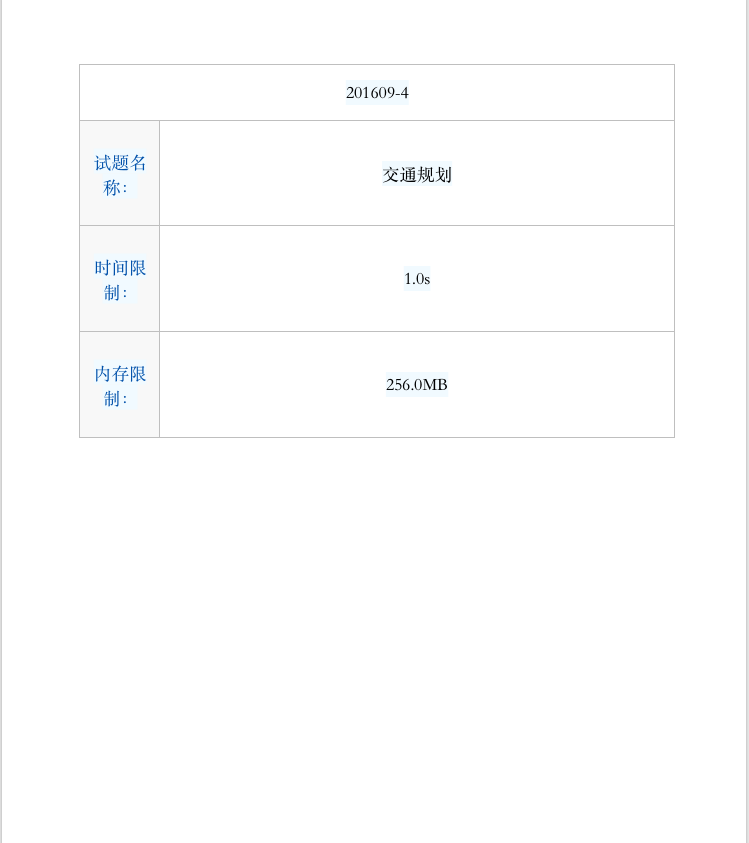
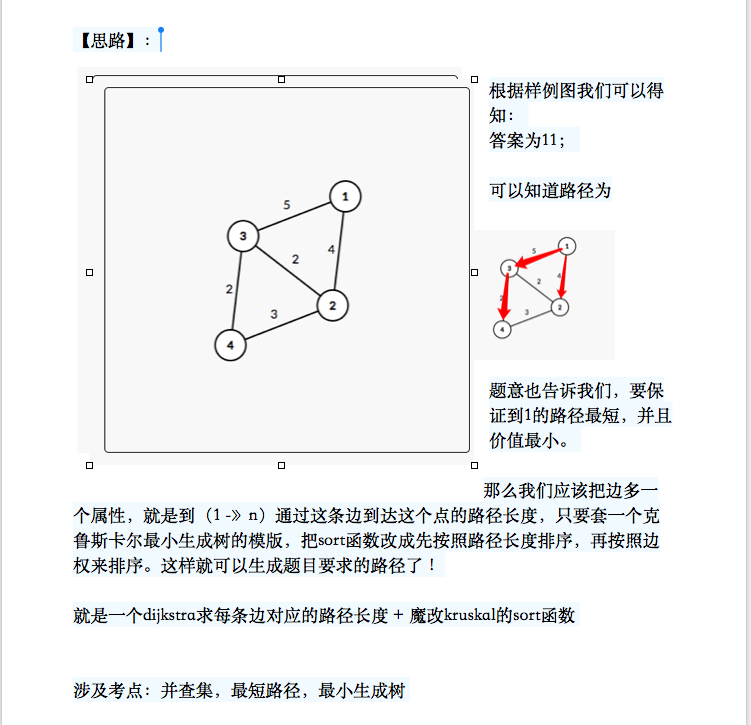
附上代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define inf 0xfffffff
int n, m;
typedef struct NODE
{
    int to;
    int cost;
    friend bool operator < (const NODE &a, const NODE &b) {
        return a.cost > b.cost;
    }
}node;
typedef struct Edge
{
    int from;
    int next;
    int to;
    int w;
    int value;
} edge;
edge maps[10000005];
int head[100050];
int dist[100050];
int vids[100050];
int cnt;
void creat ()
{
    for(int i=0; i<100050; i++)
        head[i]=-1;
    cnt=0;
}
void add(int u,int v,int w)
{
    maps[cnt].from = u;
    maps[cnt].to=v;
    maps[cnt].w=w;
    maps[cnt].value = w;
    maps[cnt].next=head[u];///一开始放置为-1，-1的条件就可以跳出
    ///下一步接着储存,head[u]的值,就是前面的位置
    head[u]=cnt++;///head[u]会得到这条线的值
}
int dijkstra(int s,int t)
{
    for(int i=0; i<100050; i++)
    {
        vids[i]=0;
        dist[i]=inf;
    }
    priority_queue<node>que;
    node begins;
    begins.to=s;
    begins.cost=0;
    que.push(begins);
    while(!que.empty())
    {
        node ends=que.top();
        que.pop();
        if(!vids[ends.to])
        {
            vids[ends.to]=1;
            dist[ends.to]=ends.cost;
            for(int i = head[ends.to]; ~i; i = maps[i].next)
            {
                int to = maps[i].to, w = maps[i].w;
                maps[i].w = ends.cost + w;
                if(!vids[to])
                {
                    node ans;
                    ans.to=to;
                    ans.cost=ends.cost+w;
                    que.push(ans);
                }
                
            }
        }
    }
    if(dist[t] == inf)
    {
        return -1;
    }
    else
    {
        return dist[t];
    }
}
bool cmp(const edge & a, const edge & b)
{
    if(a.w != b.w)
    {
        return a.w < b.w;
    }
    return a.value < b.value;
}
int pre[100050];
void Init()
{
    for(int i=1; i<=m; i++)
        pre[i]=i;
}
int finds(int x)
{
    if(pre[x]==x)
        return x;
    else
        return pre[x]=finds(pre[x]);
}
void unionjoin(int x,int y)
{
    int u=finds(x);
    int v=finds(y);
    if(u==v)
        return ;
    else
        pre[u]=v;
}
bool same(int x,int y)
{
    return finds(x)==finds(y);
}
long long kruskal()
{
    long long ans=0;
    sort(maps,maps + 2 * m,cmp);
    for(int i = 0; i< 2 * m; i++)
    {
        if(!same(maps[i].from,maps[i].to))
        {
            unionjoin(maps[i].from,maps[i].to);
            ans+=maps[i].value;
        }
        else
            continue;
    }
    return ans;
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        creat();
        for(int i = 0; i < m; i ++) {
            int u, v, w;
            scanf("%d%d%d",&u, &v, &w);
            add(u, v, w);
            add(v, u, w);
        }
        dijkstra(1, n);
        Init();
        long long re = kruskal();
        printf("%lld\n",re);
    }
    return 0;
}