2018 FJUT ACM 校赛 j题 外传：魔王打工记（一）

 

外传：魔王打工记（一）

TimeLimit:1000MS  MemoryLimit:128MB

64-bit integer IO format:%lld

 

Problem Description

话说Home_W大魔王手下有四大天王： 首席战神——赛文斯，SoftWork首席科学家——布莱克，首席军师——金金金，首席狙击手——超无聊，首席苦力——小明。

    然而，这些部下个个都是饭桶，把Home_W都快吃穷。虽然Home_W嘴上说：打工是不可能打工的，这辈子不可能打工的。烧杀抢又不会做，就只有当正义的魔王这种东西，才能维持的了生活的体面，进了魔王堡感觉像回家一样，在魔王堡的感觉比家里感觉好多了！里面个个都是人才，说话又好听，我超喜欢里面的！”但实际上，Home_W在背地里伪造了各种身份，偷偷地做一些兼职以维持生计。

    现在Home_W刚升入国家统计局工作，统计局里刚给他分配报酬1e RMB的一项工作：

给出N个整数a1,a2,a3,……，aN,问：对于任意的L,R。求序列aL,aL+1……aR的方差乘（R-L+1）2

其中方差的公式如下：

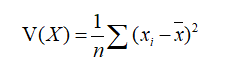
Home_W在接到工作后熟练敲起了代码，只见他摸上键盘的一瞬间天黑地暗，大地都在颤抖，星辰都在闪烁，不到一分钟就算完了。办公室里的无不起立鼓掌，领导也对其刮目相看，额外奖励了他价值1e9+7 RMB的破坏公物罚单一张。

 

 

 

Input

单组数据

开头是一个整数N,q代表N个数字，q次询问.N,q<=100,000

接下来有n个数a1,a2,a3,……an  ,（0<=ai<=10000）

再接下来q行，每行包含两个整数L,R. (1<=L<=R<=N)

 

Output

对于每个查询输出一个整数，代表方差乘（R-L+1）2

SampleInput

10 10
6 1 3 0 4 5 0 7 7 4
8 10
2 4
1 3
5 8
7 9
4 10
1 9
4 6
1 6
9 10

SampleOutput

18
14
38
104
98
356
576
42
161
9
【思路】：(此处的^,不是异或，是代表pow())
v（x）=（1/n）*∑（x[i]-(ave)sum(x)）^2
result(x)=(i/n)*(∑(x[i]-(ave)sum(x))^2))*(r-l+1)^2
n=r-l+1
result(x)=n*∑((x[i]-(ave)sum(x))^2)
(ave)sum(x)=(∑x[i])/n
result(x)=n*∑(x[i]^2-(2*x[i]*∑x[i]/n+(∑(x[i]^2))/(n^2)))
因为∑(x[i])可以视为一个常数，即可化简如下：
　　　　　 =n*∑(x[i]^2)-2(∑x[i])^2+(∑x[i])^2
　　　　　 =n*∑(x[i]^2)-(∑x[i])^2
看不懂的可以看图片：（字不好看）

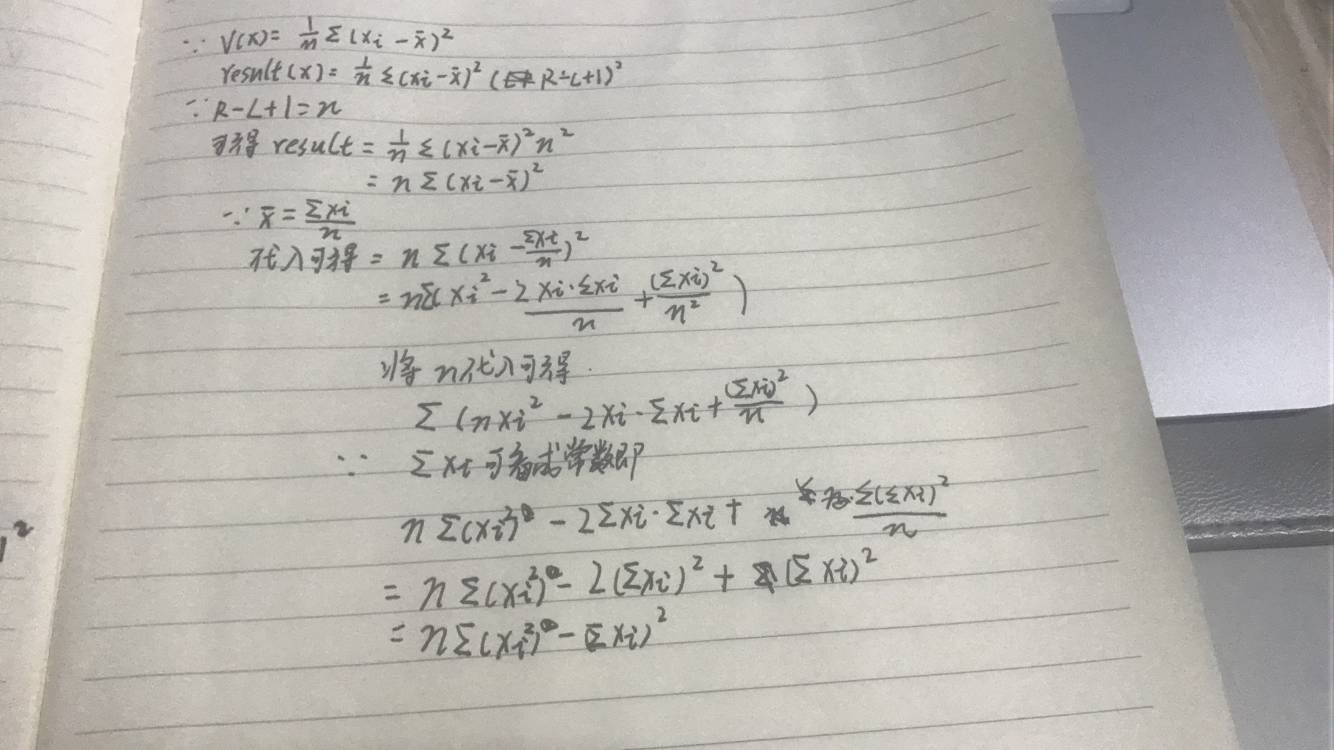
附上代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
const int MAXN = 100005;
int n,q;
int math[MAXN];
ll sum[MAXN];
ll sum2[MAXN];
int main()
{
    while(~scanf("%d%d",&n,&q))
    {memset(math,0,sizeof(math));
    memset(sum,0,sizeof(sum));
    memset(sum2,0,sizeof(sum2));
    sum[0]=0;
    sum2[0]=0;
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&math[i]);
            sum[i]=sum[i-1]+math[i];
            sum2[i]=sum2[i-1]+(math[i]*math[i]);

        }
        for(int i=1;i<=q;i++)
        {
            int l,r;
            scanf("%d%d",&l,&r);
            int num=(r-l+1);
            ll ans=num*(sum2[r]-sum2[l-1])-(sum[r]-sum[l-1])*(sum[r]-sum[l-1]);
            printf("%lld\n",ans);
        }
    }
    return 0;
}