机器学习|二进制粒子群优化算法应用于特征选择问题

1.特征选择

比如有一个M行（N+1）列的数据集，每一行代表一组数据，对于每一列，前N列代表N个特征，最后一列代表这组数据的标签。

那么，对于特征选择问题，就是要找到这N个特征的一个尽可能小的子集，然后通过这个子集中的特征进行学习，可以确保正确率较高的分类结果。（分类的结果是否正确通过查看第N+1列的标签与预测的哪组数据在哪个类里是否相同）

所以，特征选择问题本质上就是选择一个合适的0/1串。串的长度是原始数据集中的特征个数N，0是不被选择的属性，而1是被选择的属性。

2.粒子群优化算法（Particle Swarm Optimization，PSO）

这是人们由鸟类觅食的集群活动的启发而提出来的一个启发式算法。首先，我们知道寻找一个合适的0/1串最简单也最全面的方法就是暴力枚举，也就是把所有的取值都计算一遍，这样是不现实的。共有2的N次方种可能，是一个NP-Hard问题。启发式算法就是在部分解中寻找一个最优解，当然这是一个局部最优解。但是，由于它只选择了部分解，因此时间空间开销都是较小的。

粒子群优化算法的思想是：假设空间中有一些粒子随机的分布在不同的空间位置上，每个粒子有两个属性——位置和速度。这两个属性的初始值都是随机的。每个粒子维护一个自身的最优点pbest（最优指的是适应度函数取得最优时的位置值），整个粒子群维护一个全局的最优点gbest（即所有粒子的pbest对应的适应度函数最大的那一个）。然后进行迭代，迭代的过程可以描述为粒子按照自身最优pbest的方向和全局最优gbest的方向按一定比例来改变速度，继而改变本次迭代粒子到达的位置。公式如下所示：

速度公式：（w，c1，c2都是权重参数，rand是一个[0,1]的随机数，t代表迭代次数）

速度公式可以这样理解：粒子在某次迭代时的速度由三个方面决定——自身原有的速度（上一次迭代得到的速度）、自身历史最佳点的速度、全局历史最佳点的速度。这三个分量按照一定的权重合成了本次迭代的速度。

位置公式：

位置公式就是简单的匀速直线运动公式：x=x0+vt（t=1 因为一次迭代相当于经过一个时间单位）

自定义一个迭代次数，按照这个方式进行迭代最终可能得到一个局部最优解（也可能出现没到局部最优解时迭代就已经结束了的情况，所以迭代次数要定义的尽量大一些）

迭代结束时的全局最优解gbest（适应度函数取最优时的位置值）就是算法得到的解。

这里，要提一下适应度函数，它是人为制定的“最优”的标准，比如说，在粒子群优化算法应用到特征选择的问题上，适应度函数可以定义为分类准确度的大小，也可以定义为分类错误率的大小。如果定义为前者，那么适应度函数取值最大时得到的是最优解；如果定义为后者，那么适应度函数取值最小时得到的是最优解。

注意：这里每个粒子的速度和位置都是N维向量，不要把思维局限在传统的物理学问题上认为速度和位置是一个值，这是N维空间的问题，每一维都有一个值。

3.二进制粒子群优化算法（Binary Particle Swarm Optimization,BPSO）

根据前面的讲述，我们可以意识到——粒子群优化算法是一个解决连续空间问题的算法，而要想应用到特征选择问题上找到相要的0/1串，要做一些细微的修改使它能解决离散空间问题。当然，一种最简单的方法就是给位置值设定一个阈值，超过阈值就设为1，否则就设为0，这样就把连续空间的N维位置向量转换为离散空间的0/1串了。不过这样做解释起来并没有什么意义，所以二进制粒子群优化算法出现了。

它对粒子群优化算法的改进是：速度公式不变，增加了一个sigmoid函数，重新定义了位置公式。如下：

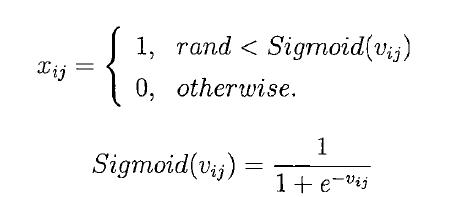
这样得到的x就是一个0/1串，gbest中为1的特征就是最终要选择的特征。

 

其他的好文档指路：

特征选择的详细介绍：https://www.cnblogs.com/zhizhan/p/4083688.html

粒子群优化算法介绍：https://blog.csdn.net/google19890102/article/details/30044945