DS博客作业06--图
1.本周学习总结 
1.1 思维导图

1.2 学习体会 💪
本章学习了图结构的相关知识,图形结构属于复杂的非线性数据结构,在实际应用中很多问题可以用图来描述。对于图结构的认识,图中元素之间的关系是多对多的;图结构的存储分为临邻接矩阵和邻接表;图的遍历分为深度遍历和广度遍历,深度遍历求出的路径不一定时最短路径,而广度遍历求出的路径一定是最短路径。
关于图的学习,可能是因为临近期末,这几周的学习比较赶,学到的知识也掌握的不是很熟练,比如最小生成树的Prim算法、Kruscal算法,最短路径Dijkstra算法、Floyd算法这几种算法掌握的不是很好,总是忘得很快,容易混淆。
2.PTA实验作业 
2.1 图着色问题
2.1.1 设计思路
int main() //主函数
输入顶点数与边数,颜色数进行建图
输入待检查的颜色分配方案的个数n
for( ;n;n--){
for i=1 to 顶点数{
输入颜色的分配方案,统计所用颜色总数num
}
若统计的颜色总数num!=题干的颜色数
则把flag由0赋为1
}
将颜色按深度遍历排序储存在数组中
for i=1 to 顶点数{
for j=1 to 顶点数{
若有相邻的颜色相同
则把flag的值由0赋为1
}
flag值已为1即已有相邻颜色相同停止循环
}
如果flag=1 输出no 否则 输出yes
2.1.2 代码截图
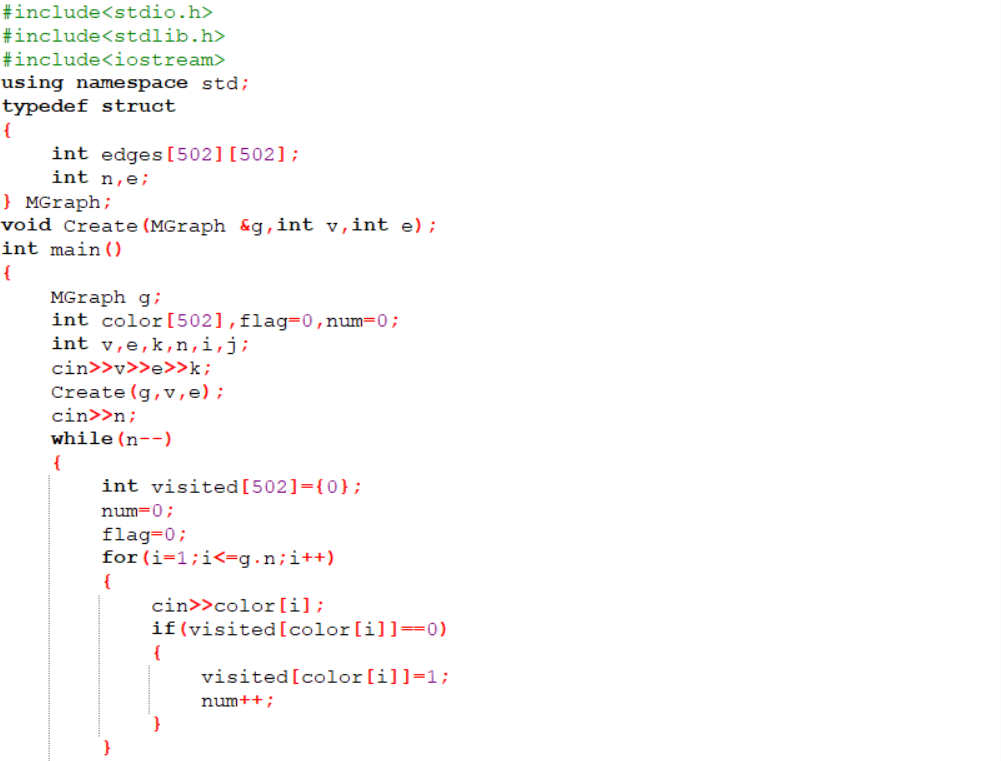


2.1.3 PTA提交列表说明。

- 计算颜色种类时,变量忘记初始化为0
- 数组上限定义不够
2.2 六度空间
2.2.1 设计思路
int main()
输入N,M;
构建邻接矩阵;
for i = 1 to N
调用BFS(i);
初始化visit数组;
计算百分比,并输出;
int BFS(int v)
定义队列q;
定义 temp, count = 1;
定义level= 0; //记录层数
定义last = V;//记录当前层数的最后一个元素
定义tail;//指向下一层最后一个元素
把v入队;
visit[v] = 1;
while (!q.empty())
取队头元素;
出队;
for i = 1 to N
if arr[temp][i] && visit[i] == 0 then
count++;
tail = i;
visit[i] = 1;
i进队;
end if
if temp == last then
level++;
修改last的值为tail;
end if
if level == 6 then
break;
返回 count;
2.2.2 代码截图


2.2.3 PTA提交列表说明。

- 自己做的时候,总有问题,一直过不了,后来参考同学的代码
- 这个代码比较简洁,运用了队列,也使用了memset函数,使初始化更加简洁
2.3 公路村村通
2.3.1 设计思路
int main()
定义 最低成本cost = 0;
输入v,e;
建图;
cost =Prim(v,e);
输出cost;
void CreateGraph(int v,int e)//用邻接矩阵表示图
初始化;
读入权值;
无向图对称;
int Prim(int v,int e)
定义min,i,j,k;
定义 lowcost[MAXVEX];
定义 cost =0;
lowcost[1] = 0; //初始化第一个权值为0,即v0加入生成树
for i=2 to v
lowcost[i] = G[1][i];//对顶点1所相邻的边进行初始化
for i=2 to v
令min等于无穷;
j = 1;
k = 0;
while( j<=v )
将lowcost[]数组最小的边赋值给min;
用k记录该边所对应的顶点;
j++;
if k==0 then //不连通
return -1;
end if;
cost += min;
lowcost[k] = 0; //将当前顶点设置为0,表示此结点已经完成任务
for j=2 to v
if lowcost[j]!=0 && G[k][j]<lowcost[j] then
//若下标为k顶点各边权值小于此前这些顶点未被加入生成树的权值
lowcost[j] = G[k][j];
end if;
返回 cost;
2.3.2 代码截图



2.3.3 PTA提交列表说明。

- 刚开始对图初始化时,令 G[i][j]=NULL ,而且 没有令min等于无穷,后来请教同学将min设为不存在边的g数组的值,以此来判断各个顶点与其他顶点是否存在边
3.上机考试错题及处理办法 
3.1 截图错题代码
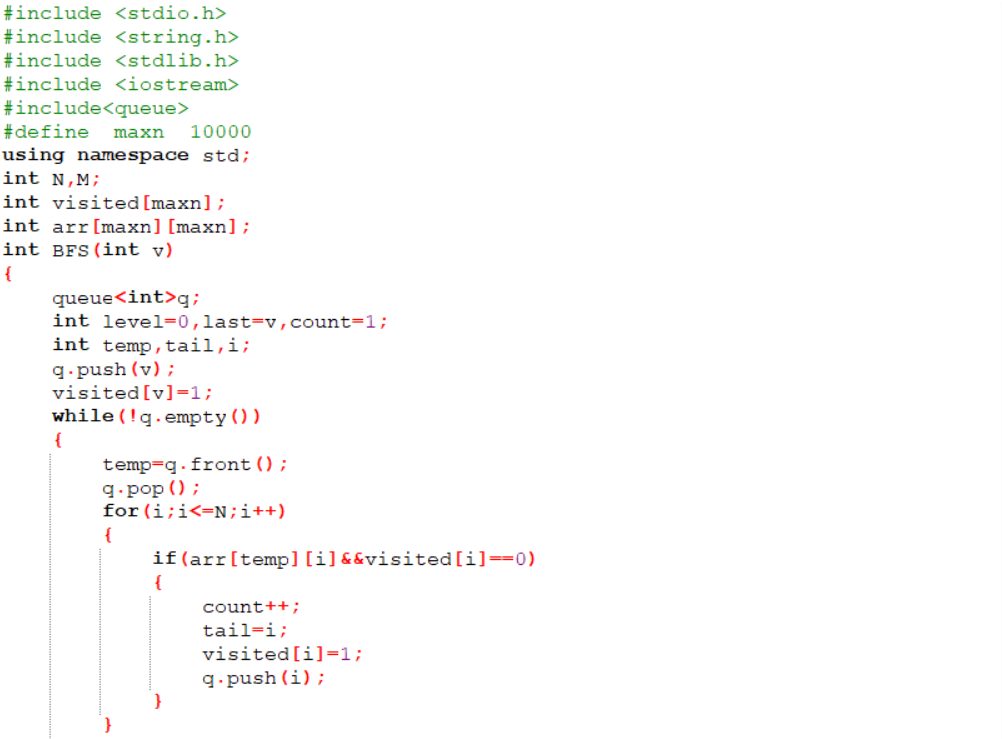

3.2 错的原因及处理方法
-
刚开始也不知道哪里错了,编译出来的答案是错的,后来看了半天发现,其中一个for循环里面i没有赋初值,导致计数并不是从1开始,导致答案错误
-
错误:







