SICP读书笔记（一）牛顿法求平方根

LispBox装完后试了一下，感觉还是不错的，于是找到了《计算机程序的构造和解释》，边学基础边练习。

书中使用的是Scheme，我依然使用CCL作为练习，专注思想的学习，同时折腾一下函数式风格。

 

实例：牛顿法求*方根

实数*方根定义：如果y²=x,且y>0,则称y为x的*方根

 

牛顿逐步逼*法求*方根步骤：

1.猜测x的*方根为 y，

2.计算y和x/y的*均值，

3.将步骤2的结果作为猜测值，

4.重复步骤2，3，直到误差允许范围

 

CCL 代码：

(defun squarex (x)
  (* x x))

(defun averagex (x y)
  (/ (+ x y) 2.0))

(defun absx (x)
  (if (< x 0) (- 0 x) x))

(defun good-enough? (x y c)
  (< (absx (- x y)) c))

(defun sqrt-improve (guess x)
  (averagex guess (/ x guess)))

(defun sqrt-iter (guess x c)
  (if (good-enough? (squarex guess) x c)
    guess
    (sqrt-iter (sqrt-improve guess x) x c)))

(defun sqrtx (x &key (c 0.001 c-supplied-p))
  (sqrt-iter x x (if (< c 0) 0.001 c)))

　　 

*方根逼*过程分析：

假设 x的*方根准确值为 a > 0，猜测值为 b > 0

则 (a - b)² ≥ 0， x = a²

=> a² - 2ab + b² ≥ 0

=> a² + b² ≥ 2ab

=> x + b² ≥ 2ab

=> a ≤ (x + b²) / 2b

=> a ≤ (x/b + b) / 2

_{由上可知，步骤2处理结果一定大于等于*方根，且仅当a = b时取等号。}

当a = b时误差为0，故符合误差要求，直接得结果。

当a ≠ b时，有 a < (x/b + b) / 2

令 b_n = (b_n-1 + x / b_n-1) / 2，b₀ > 0

则 a < b₁ = (b₀ + x / b₀) / 2，故从 b₁后一定有 a < b_n，

当 n > 1,

b_n =  (b_n-1 + x/b_n-1 ) / 2

令 d_n = b_n - b_n-1 =  (b_n-1 + x/b_n-1 ) / 2 - (2 * b_n-1 / 2)

=> 2 * d_n = b_n-1 + x/b_n-1 - 2*b_n-1 = x/b_n-1 - b_n-1 

因 x / b_n-1 = a² / b_n-1  ，且 a² ≤ a * b_n < b_n²，

=> x / b_n-1 < b_n-1² / b_n-1 = b_n-1

=> x/b_n-1 - b_n-1 < 0

=> d_n < 0

=> b_n - b_n-1 < 0

=> b_n < b_n-1

=> a < b_n < b_n-1

综上所述，当 初始值 不等于 精确值 时，使用 步骤2 迭代，返回结果会不断减小，并且一直大于 精确值。

如此理论*方根的*方应该略大于原值，但执行结果上存在小于原值的情况，可能是 浮点 精度损失导致。

---

附上：牛顿逼*法

求解某个方程，都可以将其转换为 f(x) = 0 的形式。

在图形上，表述为 函数 f(x) 与 x 轴的交点。

此时，可以任取一点作切线，切线代表了所取点的变化，它与x轴的交点便代表了 f(x) 与 x轴相交的方向。使用交点继续作切线，同理下其，最终会接*真实的交点。

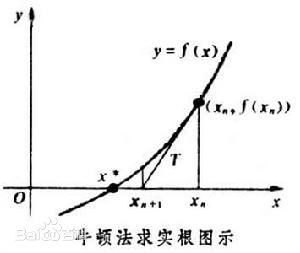
这个过程的导数形式：x_n+1 = x_n - f(x_n) / f'(x_n)

求*方根 即是 a²=y => f(x) = x² - y

求 f(x) = 0时的 x值。

f'(x) = 2 * x

=> x_n+1 = x_n - (x_n² - y) / (2 * x_n)

=> x_n+1 = (x_n² + y) / (2 * x_n)

=> x_n+1 = (x_n + y/x_n) / 2.

 

lisp自带求*方根函数 sqrt 源码：

(defun sqrt (x &aux a b)
  "Return the square root of NUMBER."
  (cond ((zerop x) x)
        ((complexp x) (* (sqrt (abs x)) (cis (/ (phase x) 2))))          
        ((minusp x) (complex 0 (sqrt (- x))))
        ((floatp x)
         (fsqrt x))
        ((and (integerp x) (eql x (* (setq a (isqrt x)) a))) a)
        ((and (ratiop x)
              (let ((n (numerator x))
                    d)
                (and (eql n (* (setq a (isqrt n)) a))
                     (eql (setq d (denominator x))
                          (* (setq b (isqrt d)) b)))))
         (/ a b))          
        (t
         #+32-bit-target
         (target::with-stack-short-floats ((f1))
           (fsqrt (%short-float x f1)))
         #+64-bit-target
         (fsqrt (%short-float x)))))