机器学习-导数
1、概念解释
(1)关于求导
求导是微积分中的重要概念之一,它可以用来计算函数在某一点处的变化率(斜率),以及函数的最大值、最小值等。
对于一个函数y=f(x),它在某一点x₀处的导数(即斜率)定义为:
f'(x₀) = lim (h→0) [f(x₀+h) - f(x₀)] / h
其中lim表示当h趋近于0时的极限。这个式子的意思是,我们考虑函数f(x)在x₀处左右两边的取值,当自变量增加一个无穷小量h时,函数值相应地增加f(x₀+h)-f(x₀)。那么,当h趋近于0时,f(x)在x₀处的变化率就可以近似地表示为这个差商的极限值。这个极限就是函数在x₀处的导数f'(x₀)。
一般来说,如果一个函数在某一点x₀处可导,那么它在这个点的导数就等于这个极限值。如果一个函数在某些点不可导,那么它在这些点处的导数不存在。当函数在某一点的导数为0时,这个点就可能是该函数的局部极值点。
(2)求导公式
求导的公式可以根据函数的类型和性质而变化。下面是一些常见函数的求导公式:
-
常数函数:如果y = c,其中c为常数,则导数为0,即dy/dx = 0。
-
幂函数:如果y = x^n,其中n为实数,则导数为dy/dx = nx^(n-1)。
-
指数函数:如果y = e^x,则导数为dy/dx = e^x。
-
对数函数:如果y = logₐ(x),其中a为底数,则导数为dy/dx = 1 / (x ln(a))。
-
三角函数:
- 正弦函数:如果y = sin(x),则导数为dy/dx = cos(x)。
- 余弦函数:如果y = cos(x),则导数为dy/dx = -sin(x)。
- 正切函数:如果y = tan(x),则导数为dy/dx = sec²(x)。
-
反三角函数:
- 反正弦函数:如果y = arcsin(x),则导数为dy/dx = 1 / √(1 - x²)。
- 反余弦函数:如果y = arccos(x),则导数为dy/dx = -1 / √(1 - x²)。
- 反正切函数:如果y = arctan(x),则导数为dy/dx = 1 / (1 + x²)。
-
复合函数:如果y = f(g(x)),则根据链式法则,导数可以计算为dy/dx = f'(g(x)) * g'(x),其中f'表示f的导数,g'表示g的导数。
2、基本演算


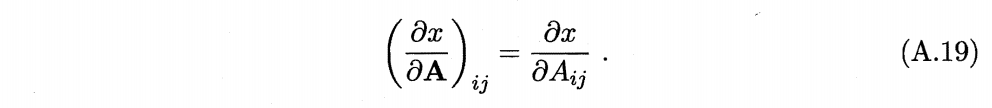









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本