HDU 3265 扫描线（矩形面积并变形）

Posters

Time Limit: 5000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 5230    Accepted Submission(s): 1220

Problem Description

Ted has a new house with a huge window. In this big summer, Ted decides to decorate the window with some posters to prevent the glare outside. All things that Ted can find are rectangle posters. 

However, Ted is such a picky guy that in every poster he finds something ugly. So before he pastes a poster on the window, he cuts a rectangular hole on that poster to remove the ugly part. Ted is also a careless guy so that some of the pasted posters may overlap when he pastes them on the window. 

Ted wants to know the total area of the window covered by posters. Now it is your job to figure it out.

To make your job easier, we assume that the window is a rectangle located in a rectangular coordinate system. The window’s bottom-left corner is at position (0, 0) and top-right corner is at position (50000, 50000). The edges of the window, the edges of the posters and the edges of the holes on the posters are all parallel with the coordinate axes. 

 

 

Input

The input contains several test cases. For each test case, the first line contains a single integer N (0<N<=50000), representing the total number of posters. Each of the following N lines contains 8 integers x1, y1, x2, y2, x3, y3, x4, y4, showing details about one poster. (x1, y1) is the coordinates of the poster’s bottom-left corner, and (x2, y2) is the coordinates of the poster’s top-right corner. (x3, y3) is the coordinates of the hole’s bottom-left corner, while (x4, y4) is the coordinates of the hole’s top-right corner. It is guaranteed that 0<=xi, yi<=50000(i=1…4) and x1<=x3<x4<=x2, y1<=y3<y4<=y2.

The input ends with a line of single zero.

 

 

Output

For each test case, output a single line with the total area of window covered by posters.

 

 

Sample Input

2

0 0 10 10 1 1 9 9

2 2 8 8 3 3 7 7 0

 

 

Sample Output

56

 

 

Source

2009 Asia Ningbo Regional Contest Hosted by NIT

 

 

题目意思：

有n张回字形海报，然后求总面积（覆盖面积仅算一次）

 

思路：

矩形面积并的变形。

 

 

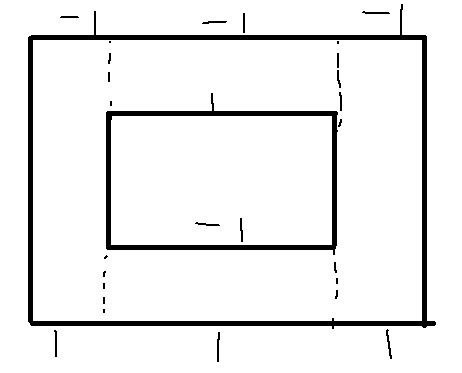
以如图所示建边插入线段树，就和普通的扫描线一样了

 

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
#include <set>
using namespace std;

#define N 50005
#define ll root<<1
#define rr root<<1|1
#define mid (a[root].l+a[root].r)/2

int max(int x,int y){return x>y?x:y;}
int min(int x,int y){return x<y?x:y;}
int abs(int x,int y){return x<0?-x:x;}

struct node{
    int l, r;
    int val;
    __int64 sum;
}a[N*16];

struct Line{
    int x1, x2, y;
    int val;
    Line(){}
    Line(int a,int b,int c,int d){
        x1=a;
        x2=b;
        y=c;
        val=d;
    }
}line[N*8];

bool cmp(Line a,Line b){
    return a.y<b.y;
}

int xx[N*4];
int n, m;

int b_s(int key){
    int l=1, r=m;
    while(l<=r){
        int mm=(l+r)/2;
        if(xx[mm]==key) return mm;
        else if(xx[mm]<key) l=mm+1;
        else if(xx[mm]>key) r=mm-1;
    }
}

void build(int l,int r,int root){
    a[root].l=l;
    a[root].r=r;
    a[root].sum=a[root].val=0;
    if(l==r) return;
    build(l,mid,ll);
    build(mid+1,r,rr);
}

void up(int root){
    if(a[root].val) a[root].sum=xx[a[root].r+1]-xx[a[root].l];
    else if(a[root].l==a[root].r) a[root].sum=0;
    else a[root].sum=a[ll].sum+a[rr].sum;
}

void update(int l,int r,int val,int root){
    if(l>r) return;
    if(a[root].l==l&&a[root].r==r){
        a[root].val+=val;
        up(root);
        return;
    }
    if(r<=a[ll].r) update(l,r,val,ll);
    else if(l>=a[rr].l) update(l,r,val,rr);
    else{
        update(l,mid,val,ll);
        update(mid+1,r,val,rr);
    }
    up(root);
}
main()
{
    int x1, y1, x2, y2, x3, y3, x4, y4;
    int i, j, k;
    while(scanf("%d",&n)&&n){
        k=0;
        m=1;
        for(i=0;i<n;i++){
            scanf("%d %d %d %d %d %d %d %d",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4);
            line[k++]=Line(x1,x3,y1,1);
            line[k++]=Line(x1,x3,y2,-1);
            line[k++]=Line(x3,x4,y1,1);
            line[k++]=Line(x3,x4,y3,-1);
            line[k++]=Line(x3,x4,y4,1);
            line[k++]=Line(x3,x4,y2,-1);
            line[k++]=Line(x4,x2,y1,1);
            line[k++]=Line(x4,x2,y2,-1);
            xx[m++]=x1;
            xx[m++]=x2;
            xx[m++]=x3;
            xx[m++]=x4;
        }
        sort(xx+1,xx+m);
        m=unique(xx+1,xx+m)-xx-1;
        sort(line,line+k,cmp);
        build(1,m,1);
        __int64 ans=0;
        for(i=0;i<k-1;i++){
            update(b_s(line[i].x1),b_s(line[i].x2)-1,line[i].val,1);
            ans+=a[1].sum*(__int64)(line[i+1].y-line[i].y);
        }
        printf("%I64d\n",ans);
    }
}