机器学习技法(林轩田)学习笔记:Lecture 13 & Lecture 14
Lecture 13: Deep Learning
Autoencoder
autoencoder是深度学习中一种常用的初始化权重的方法。
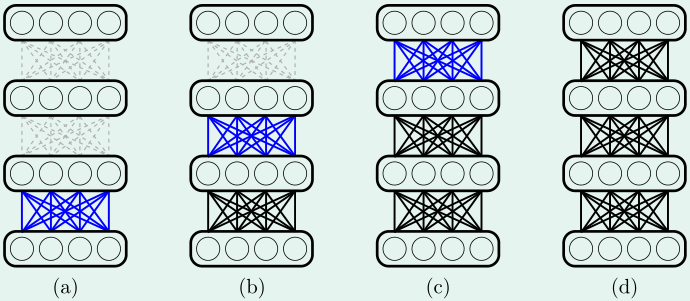
如上图所示,首先,从第0~1层的权重开始,一层层用autoencoder初始化每两层之间的权重,然后再使用训练集对整个网络进行训练
autoencoder是如何初始化每两层之间的权重呢?
我们希望初始化权重后,每一层输入信息并传递给下一层后,能最大程度地保留这些信息
对于一个两层的神经网络(输入\(d+1\)维,输出\(d\)维,隐含层神经元个数(包括偏置)为\(\tilde d+1(\tilde d<d)\))而言,如果这个网络能保证输出非常近似于输入,那么输入到隐含层的过程就最大程度上保留了原始信息。
Basic Autoencoder
假设现在要初始化第\(l-1\)层到第\(l\)层的权重,第l-1层有结点(含偏置)\(d^{(l)}+1\),第l层有结点(含偏置)\(d^{(l+1)}+1\)

最简单的autoencoder就是训练一个输入\(d^{(l)}+1\)维,隐含层有结点(含偏置)\(d^{(l+1)}+1\)个,输出结点数\(d^{(l)}\)个的神经网络,其中,隐含层激励函数为tanh,输出层激励函数为线性函数,如上图所示。
另外,这个神经网络有正则化:\(w_{ij}^{(1)}=w_{ji}^{(2)}\)(不过这个特别的正则化会使梯度下降更加复杂)
训练完这个网络后,第l-1层到l层的参数就初始化为:这个网络输入层到隐含层的参数
Denoising Autoencoder
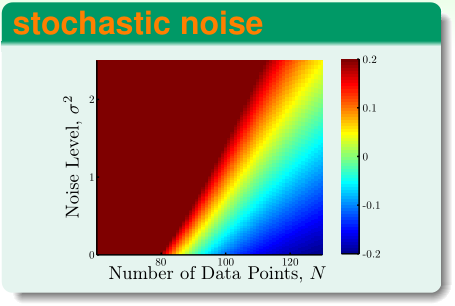
在机器学习基石中,我们已经了解了,训练样本的噪声\(\sigma^2\)越大,越容易引发过拟合。
为了解决这个问题,在用autoencoder初始化每两层之间的参数时,我们给构造的两层神经网络的输入\(x\)添加随机的噪声,使之变成\(\tilde x\),然后用\(\{(\tilde x,x)\}\)作训练集训练这个网络
Principal Component Analysis
Ng在Coursera的machine learning和CS229都讲过了PCA,但是技法的这节课从新的角度——linear autoencoder解释了PCA
考虑一种linear autoencoder,之前我们构造的两层神经网络,隐含层的激励函数是tanh,现在我们把它替换成线性激励函数,另外这个网络没有偏置。
设该网络输入d维,隐含层结点有\(\tilde d\)个\((\tilde d<d)\),输出d维。这样,这个两层网络的第k个输出可以表示为:
因为这个网络有特别的正则化:\(w_{ij}^{(1)}=w_{ji}^{(2)}=w_{ij}\),所以:
我们令\(W\in\mathbb R^{d\times \tilde d},W_{ij}=w_{ij}\),则:
那么这个网络在给定输入为x时,均方误差为:
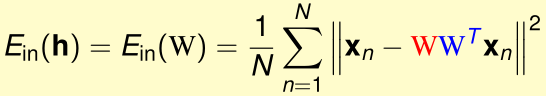
其中\(WW^T\)是实对称阵,我们通过正交变换的方式将其对角化:
\(V\)是正交阵,其中每个列向量都是一个特征向量,\(\Gamma\)是对角阵,其第i个主对角元是V的第i个列向量(特征向量)对应的特征值
因为\(r(WW^T)\leq \min(r(W),r(W^T))\leq \tilde d\),\(r(V)=d\),所以
而\(\Gamma\)是对角阵,这表明它最多有\(\tilde d\)个非零主对角元
\(WW^Tx_n=V\Gamma V^Tx_n\),相当于是用\(V^T\)对\(x_n\)作正交变换后,得到新的向量,保留其中\(r(\Gamma)\)个维度后,再用\(V\)进行逆向的正交变换将它还原回去
当给定输入为x时,这个神经网络的均方误差为:
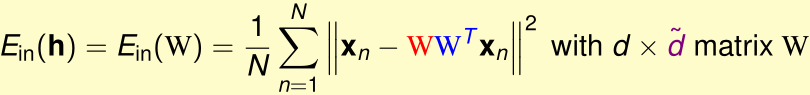
现在我们希望\(\min_wE_{in}(W)\),这等价于:
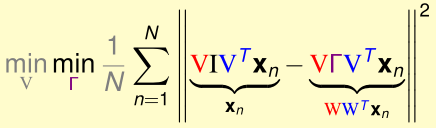
首先优化内层的\(\min_\Gamma(\cdots)\):
(正交变换V保范数)
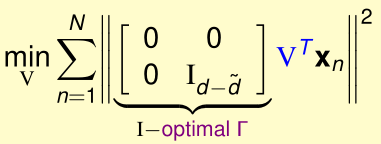
这相当于\(=\min_\Gamma\frac 1 N\sum_{n=1}^N\|(I-\Gamma) v_n\|^2\),\(v_n\)是固定的向量,显然我们希望\(\Gamma\)主对角线上1的个数越多越好,其他的主对角元都是0,那么最多有\(\tilde d\)个1,不失一般性,\(\Gamma\)可以表示为:
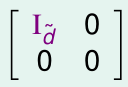
如果有其他形式的\(\Gamma\),把V的对应列交换一下就和上面这个形式一样了
下面,我们要最优化外层的\(\min_V(\cdots)\):
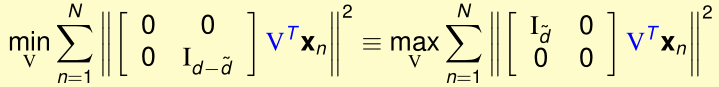
先看最特殊的情况:\(\tilde d=1\),此时只有\(V^T\)的第一行\(v^T\)起作用,优化目标变成了:

这是一个带等式约束条件的最优化问题,我们用拉格朗日乘数法构造拉格朗日函数\(\mathcal L\),令\(\frac{\partial \mathcal L}{\partial v}=0\)可以得到:
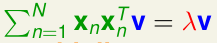
可见,v是\(\sum_{n=1}^Nx_nx_n^T=X^TX\)的特征向量,最优的向量v是\(X^TX\)的特征值最大的特征向量
推广到一般情形,可以证明,最优的向量\(v_1,\cdots,v_{\tilde d}\)是\(X^TX\)的特征值最大的前\(\tilde d\)个线性无关的特征向量,这和CS229中,用方差最大化推导PCA得到的结果是一样的。
Lecture 14: Radial Basis Function Network
RBF Network Hypothesis
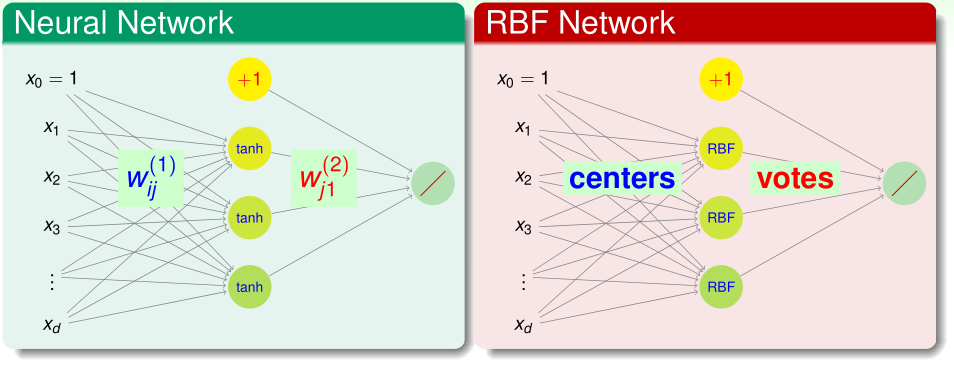
对于一般的两层的神经网络而言,其隐含层每个神经元j接收的\(s\)是所有输入\(x_i\)与参数\(w_{ij}^{(2)}\)加权求和的结果,我们可以视\(s\)为输入向量\(x\)与参数向量\(w_j\)的内积的结果,隐含层每个神经元j的输出是其s经激励函数处理后的值
而Full RBF Network的假设函数为:
即,输入的特征\(x\)与第n个训练样本的特征\(x_n\)越相似,那么第n个训练样本的真实输出\(y_n\)对结果的影响越大。
而一般来说,在full RBF network中,只有距离\(x\)最近的训练样本的\(x_n\)对应的\(y_n\)会对最终的预测输出起决定性作用。因此在实践中,一般\(h(x)\)被简化为直接选择与\(x\)距离最近的\(x_n\)对应的\(y_n\)作为预测输出
Interpolation by Full RBF Network
我们现在考虑用full RBF Network实现回归,exp(...)前的系数不再是\(y_n\),而是一个参数\(\beta_n\),则假设函数为:
我们可以看作是输入特征\(x_n\)经过特征变换得到\(z_n\),其中
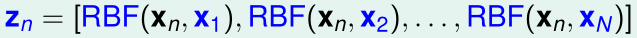
\(h(x)\)可以看作是一个关于\(z\)的线性函数,这是\(\mathcal Z\)空间里的线性回归模型:
我们用训练集\(\mathcal D=\{(z_n,y_n)\}_{n=1}^N\)来训练\(h(x)\)
回顾之前学过的最小二乘法,设\(Z=(z_1,\cdots,z_N)^T\),我们可以得到最优的\(\beta\)的解析解:
在本问题中,Z是\(N\times N\)方阵,而且显然是实对称阵,\(Z^T=Z\)(这个Z与之前SVM里高斯核的矩阵K是一样的)
如果所有的\(x_n\)都不同的话,Z就是可逆的。此时\(\beta\)可以化简为:
可见,
\(g(x_1)=\beta^Tz_1=y^T(Z^{-1})^T\)(\(Z^T\)第一列)\(=y^TZ^{-1}\)(\(Z\)第一列)=\(y^T(1,0,\cdots,0)^T=y_1\)
类似地可以得到\(g(x_n)=y_n\)
所以这个full RBF Network的\(E_{in}=0\),在机器学习中这并非好事,它表明很有可能这个模型发生了过拟合
因此我们要引入正则化项:
在岭回归中,原始特征x被特征变换映射到无限维的空间上,其\(\beta=(K+\lambda I)^{-1}y\),而这里full RBF Network则是把x被特征变换映射到有限的N维的空间上,所以二者的\(\beta\)的解析解稍有区别
除此以外,还有一种正则化的方法。我们希望像SVM那样,只有少量的训练样本充当support vector决定着最终的假设函数
这里,我们通过K-means聚类将所有训练样本分成M个簇,每个簇的聚类中心为\(\mu_m\),每个簇对应的输出值为\(y_n\),则假设函数可以表示为
我们可以看作是将输入特征x经特征变换\(\Phi(x)\)映射到:
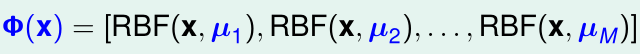
则\(h(x)=\beta^T \Phi^T(x)\),这是一个线性回归模型,我们用训练集\(\mathcal D=\{(\Phi(x_n),y_n)\}_{n=1}^N\)训练它即可。
使用K-means聚类的RBF Network的算法流程如下:


