机器学习技法(林轩田)学习笔记:Lecture 11 & Lecture 12
Lecture 11: Gradient Boosted Decision Tree
Adaptive Boosted Decision Tree
From Random Forest to AdaBoost-DTree

在随机森林中,我们通过特殊的bootstrap方法产生了T个\(\tilde{\mathcal D_t}\),并用它们分别训练T个决策树\(g_t\),最终的假设函数G是T个\(g_t\)的uniform blending
现在我们希望把adaboost套用到决策树上,Adaboost-DTree在第t次迭代时,首先对所有训练样本重新确定它们的权重\(u_i^{(t)}\),然后用加权误差来跑决策树算法,然而这样做需要修改原有的决策树算法,很复杂。
为了沿用以前的决策树算法,我们把它看作一个黑盒,不改变原有的决策树算法。只需修改bootstrap过程,让每次re-sample是有权重的随机采样,抽到第i个训练样本的概率是\(ku_i^{(t)}\)
另外,在adaboost-dtree中,和adaboost类似,我们还要确定每个\(g_t\)的权重\(\alpha_t\);之前我们说过,对于一个fully-grown tree而言,如果每个样本的输入\(x^{(i)}\)都不同,那么其\(E_{in}=0\),即\(\epsilon_t=0\),这会导致\(\alpha_t=+\infty\)
为了避免这种情况的发生,我们要想办法让单个决策树变得弱一点,比如用之前说过的prune的方法,或者直接限制树的高度
考虑adaboost-dtree的一种极端情况:决策树是C&RT,且高度\(\leq 1\),此时最多只有一个内部结点(根结点),其条件:
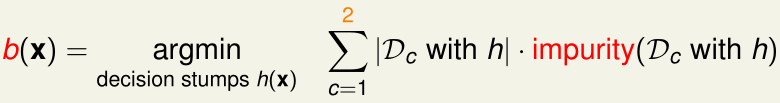
如果是二分类问题,且impurity采用二分类的0/1误差,那么这个Adaboost-Dtree就相当于是一般的adaboost(adaboost-stump)了
可见,adaboost-stump是adaboost-dtree的特殊情形
Optimization View of AdaBoost
Example Weights of AdaBoost
我们回顾adaboost中,\(u_n\)(第n个样本\(x_n\)的权重),从第t轮的\(u_n^{(t)}\)更新到第t+1轮\(u_n^{(t+1)}\)的过程:
-
初始化:所有\(u_n^{(1)}=\frac 1 N\)
-
![]()
第一步到第二步是根据:预测分类错误时\(y_n\neq g_t(x_n),y_n= g_t(x_n)=-1\),预测分类正确时\(y_n= g_t(x_n),y_ng_t(x_n)=1\)
第二步到第三步用到了\(\blacklozenge_t^{(...)}=\exp(\ln (\blacklozenge_t^{(...)}))=\exp((...)\ln \blacklozenge_t)\);
其中,\(\alpha_t=\ln \blacklozenge_t\),也就是最终linear blending时\(g_t\)的权重
则有:
最终我们得到的假设函数\(G(x)=\mathrm{sign}(\sum_{t=1}^T\alpha_tg_t(x))\)
为了方便起见,我们称\(\sum_{t=1}^T\alpha_tg_t(x)\)为voting score(对应于之前单个假设函数的\(s=w^Tz\)),voting score是T个\(g_t(x)\)的加权线性组合,我们可以把\(g_t(x)\)看作是某种对输入特征x的特征变换\(\Phi_t(x)\)
回忆一下Lecture 1 SVM中点到决策边界的距离公式:
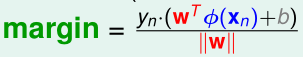
voting score可以看作是没有归一化的,点到决策边界的距离。而\(y_n\cdot\)(voting score)就是带符号的voting score,\(y_n\cdot\)(voting score)是负的,表示分类错误;否则表示分类正确。
所以我们希望\(y_n\cdot\)(voting score)是正的,且越大越好,这等价于\(\exp(-y_n\cdot\)(voting score))越小越好,也就是说我们要最小化\(u_n^{(T+1)}=\exp(-y_n\cdot\)(voting score))
所以说adaboost的过程实际上就是最小化\(\sum_{n=1}^N u_n^{(T+1)}\)的过程
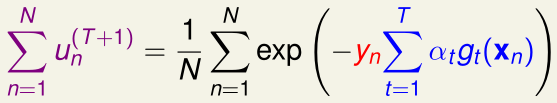
这里我们令\(s_n=\sum_{t=1}^T\alpha_tg_t(x_n)\),那么我们要最小化的就是\(\sum_{n=1}^N\exp (-y_ns_n)\),我们可以将\(\exp (-y_ns_n)\)视为adaboost的单点误差函数\(\hat {err}_{ADA}(s,y)\),我们称其为指数误差(exponential error measure)
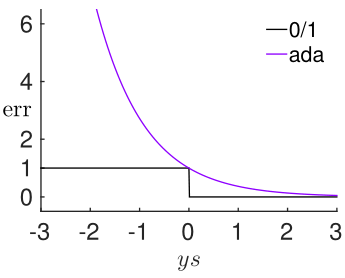
指数误差与0/1误差的图像如上图所示,可见指数误差函数是一个凸函数,并且完全"盖住"了0/1误差函数,adaboost通过最小化指数误差,来给0/1误差确定一个很小的上界,从而实现二分类
Gradient Descent on AdaBoost Error Function
回忆一下之前的梯度下降算法,在第t次迭代时,我们希望寻找一个单位方向向量\(v\),沿着\(v\)下降,使得\(E_{in}\)下降幅度最大(下面的推导过程使用了泰勒展开):

在adaboost中的第t次迭代,我们则是希望找到一个函数\(h(x)\)充当\(g_t(x)\)(对应于梯度下降里的单位方向向量\(v\)),使得:
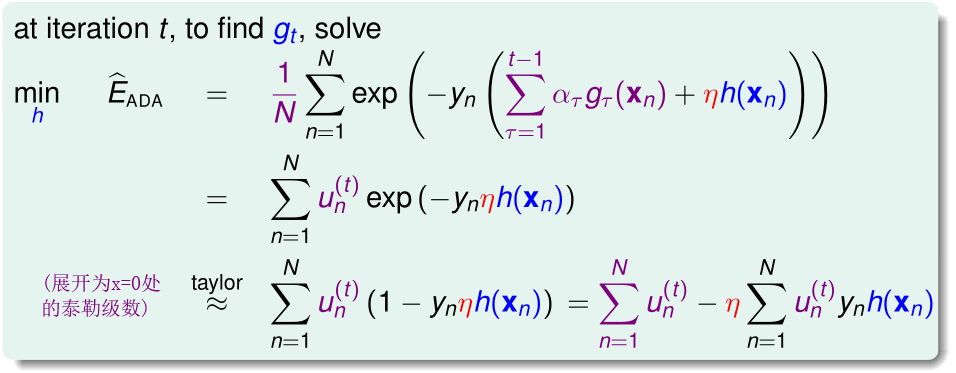
因为\(u_n^{(t)}\)都是已经求出来的已知量,\(\eta\)是固定的量,则此时优化目标等价于:
如果是二分类问题,那么\(y_n,h(x),g_{\tau}(x)\in\{-1,1\}\)
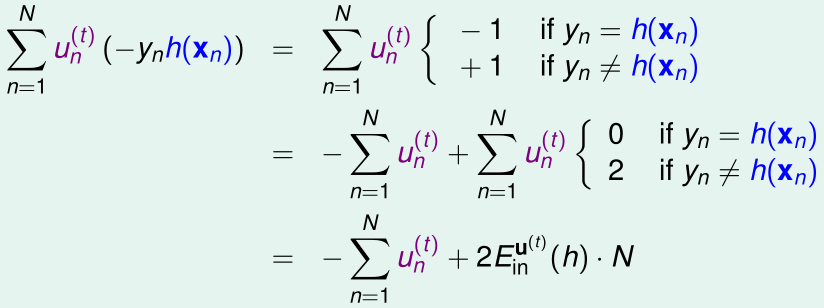
所以
因为\(u_n^{(t)}\)都是已经求出来的已知量,N是已知常数,则此时优化目标等价于:
这个优化过程就是通过adaboost的基算法\(\mathcal A\)实现的,\(\mathcal A\)找到最优的\(h\)充当\(g_t\)
在\(g_t\)找到后,我们还需要找合适的\(\eta\),使得\(\hat E_{ADA}\)减小幅度最大

(我们称这种步长\(\eta\)不固定,每次寻找下降最多的\(\eta\)的梯度下降叫最速梯度下降法)
我们看\(\hat E_{ADA}\)和式内的\(u_n^{(t)}\exp(-y_n\eta g_t(x_n))\):

而加权错误率:
所以有:
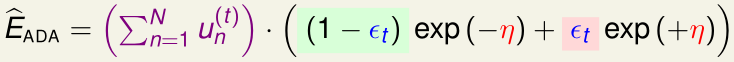
我们令\(\frac{\partial \hat E_{ADA}}{\partial \eta}=0\),可得在给定\(g_t\)时\(\hat E_{ADA}\)最小的\(\eta_t=\ln\sqrt{\frac{1-\epsilon_t}{\epsilon_t}}\),这就是\(g_t\)在最终linear blending时的权重\(\alpha_t\)
Gradient Boosting
Gradient Boosting for Arbitrary Error Function
上一节,我们把adaboost写成一个优化问题的形式,其中,每次迭代(第t次迭代)的优化目标是
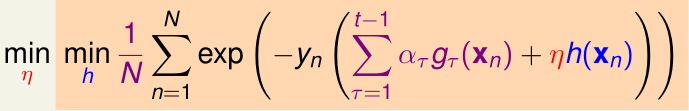
最终最优化该问题得到的\(h(x)=g_t(x),\eta=\alpha_t\) (\(g_t\)的权重)
adaboost是二分类算法,它的每个基假设函数\(g/h\)(以及训练样本的\(y_n\))都是输出-1或1,单点误差是exponential error measure
Gradient Boost把它推广到更一般的形式:每个基假设函数(以及训练样本的\(y_n\))都是输出实数值,以及其他类型的单点误差err,那么每次迭代的优化目标变成了:
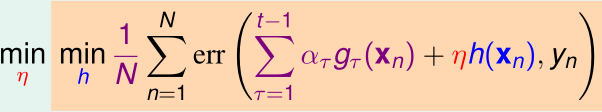
例如,现在gradient boost要解决一个回归问题,单点误差\(err(s,y)=(s-y)^2\):
首先,我们要最优化内层的h;类似adaboost,我们先把\(\min_h(\cdots)\)内的(...)展开为x=0处的泰勒级数:
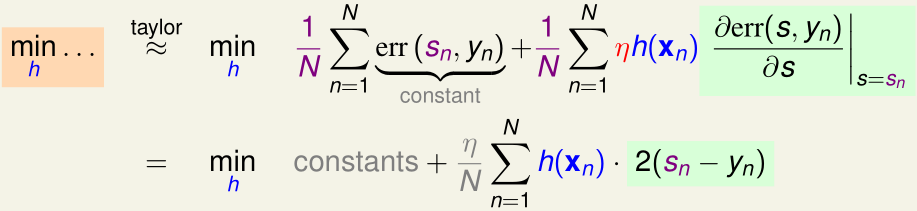
(其中,\(s_n=\sum_{\tau=1}^{t-1}\alpha_\tau g_\tau(x_n)\))
以上\(min_h(\cdots)\)的优化目标相当于
\(\min_h \sum_{n=1}^N h(x_n)\cdot 2(s_n-y_n)\)
如果我们不对h的值域作任何限制,那么得到的最优的\(h(x_n)=-\infty\cdot(s_n-y_n)\),这样\(\min_h(\cdots)=-\infty\)(注意adaboost没有这个问题,因为\(h_{adaboost}\in\{-1,1\}\))
注意到,我们并不关心h输出的比例是多少,即,我们得到h和2h,3h,...是一回事,因为对应的\(\eta\)的比例跟着改变就好了,所以我们不妨在之前的优化目标内加一个惩罚项,来约束\(h\)的大小
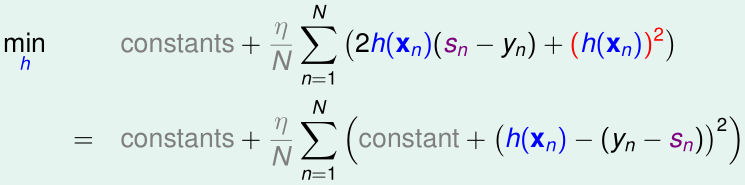
(第一步到第二步用了配方)
这个新的优化目标非常像线性回归的优化目标(均方损失函数),于是我们可以把N个\((x_n,y_n-s_n)\)当作训练样本,通过线性回归得到h,那么\(g_t=h\)
在确定了\(g_t=h\)后,我们要求出最优的\(\eta\)来最小化外层\(\min_\eta(\cdots)\)
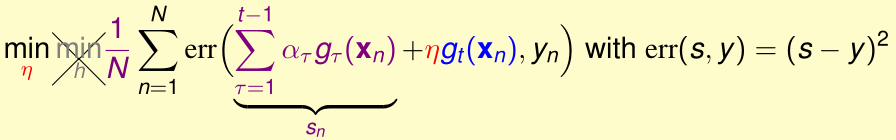
令\(s_n=\sum_{\tau =1}^{t-1} \alpha_\tau g_\tau (x_n)\),则上式变成
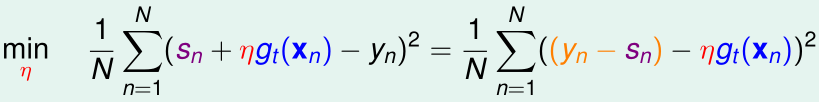
这可以看作是关于参数\(\eta\)的单变量线性回归,N个训练样本为\((g_t(x_n),y_n-s_n)\),输入特征可以看作是原始特征\(x_n\)经特征变换\(g_t\)得到的
通过这个单变量线性回归,我们能得到最优的参数\(\eta\),那么\(\alpha_t=\eta\)
我们把以上内容总结起来,可以得到Gradient Boosted Decision Tree (GBDT)算法:
初始化:\(s_1=\cdots=s_N=0\)
for t=1,2,...,T:
____(1)通过基算法\(\mathcal A\)(经过pruned的回归版C&RT)获得\(g_t\),其中训练集\(\mathcal D\)由N个样本\((x_n,y_n-s_n)\)组成
____(2)通过单变量线性回归得到\(\alpha_t\),其中训练集\(\mathcal D\)由N个样本\((g_t(x_n),y_n-s_n)\)组成
____(3)更新:\(s_n\gets s_n+\alpha_tg_t(x_n)\)
最终得到\(G(x)=\sum_{t=1}^T\alpha_tg_t(x)\)
Lecture 12: Neural Network
Neural Network Hypothesis
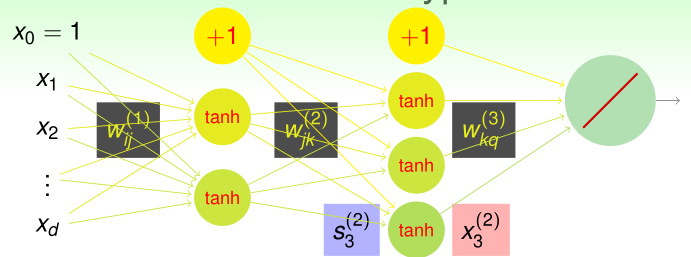
假设神经网络共有L层,其中,输入\(x_0=1,x_1,\cdots,x_d\)是第0层,输出是第L层,前L-1层中,每一层第0个神经元的输出x都是1,作为额外的偏置
第l-1到第l层的权重矩阵\(W\)是一个\((d^{(l-1)}+1)\times d^{(l)}\)大小的矩阵:
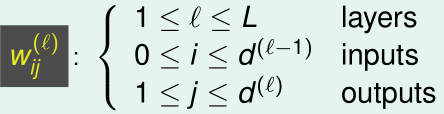
\(w_{ij}^{(l)}\)是第l-1层第i个神经元的输出到第l层第j个神经元的权重
那么第l层第j个神经元的score(第l-1层的输出值加权之和)就是
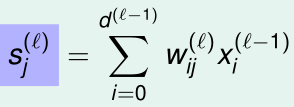
那么第l层第j个神经元的输出(其score经激励函数得到的结果)就是
-
\(j\geq 1\)时:
![]()
-
\(j=0\)时,\(x_j^{(l)}=1\)
第1~L-1层的激励函数都是tanh,第L层激励函数是线性函数y=x
Neural Network Learning
这个神经网络的误差函数使用平方误差:\(e_n=(y_n-NNet(x_n)^2)\),现在我们需要求出\(\frac{\partial e_n}{\partial w_{ij}^{(l)}}\),然后用梯度下降来最优化所有的W
我们设\(\delta_j^{(l)}=\frac{\partial e_n}{\partial s_j^{(l)}}\),则:
其中,
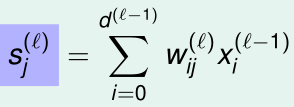
所以\(\frac{\partial s_j^{(l)}}{\partial w_{ij}^{(l)}}=x_i^{(l-1)}\)
则:
下面我们求出\(\delta_j^{(l)}\),先回忆一下,\(s_j^{(l)}\)是怎么一步步贡献到\(e_n\)的:
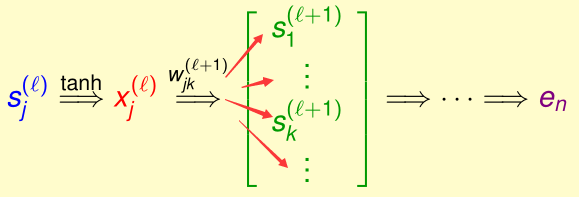
所以
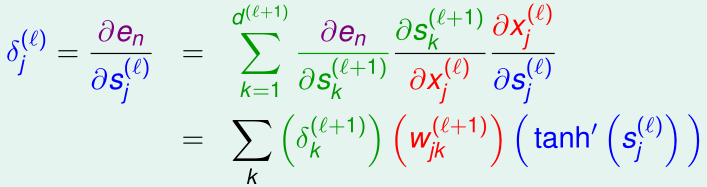
因此,如果我们得到了\(\delta_j^{(l+1)}\),便能得到\(\delta_j^{(l)}\),所以我们可以从最后一层开始倒着一层层求出\(\delta_j^{(l)}\)
据此我们可以得到一个基本的神经网络算法(Ng在Coursera和CS229里都讲得很清楚了,这里不赘述):

Optimization and Regularization
神经网络的损失函数是一个复杂的非凸函数,优化时很容易陷入局部最优点,因此恰当地对所有参数\(w\)初始化是非常重要的。一般要把所有参数\(w\)随机地在一个很小的范围内初始化(如果初始时参数\(w\)太大,其对应梯度就很小,学习就会很困难)
从VC理论的角度看,神经网络的VC维\(d_{VC}=O(VD)\),其中,V是神经元数量,D是权重参数的数量
当神经网络的层数很深、神经元很多时,其VC维就很大,优点是这样的神经网络的假设函数非常强大,缺点是非常容易过拟合,因此我们需要加入正则化
最简单的方法是在损失函数里加入L2正则化项:\(\sum(w_{ij}^{(l)})^2\)
然而L2正则化项的问题是,它是按比例缩小参数大小的,比如:当\(w_{ij}^{(l)}\)很大时,其收缩程度很大,反之则收缩程度很小,而我们希望让最终的\(W\)是稀疏的,这种按比例缩小参数,是很难让接近0的那些\(w_{ij}^{(l)}\)变成0的
然而,L1正则化:\(\sum|w_{ij}^{(l)}|\)是不可导的,所以也不适用
因此我们只能对原始的L2正则化项做修改,让很大的和很小的\(w_{ij}^{(l)}\)都能得到同等程度的收缩:
另一种正则化的方法是early stopping,因为神经网络训练迭代次数越多,相当于给它寻找最优值提供更多可能性,VC维也就更大了,所以用更小的迭代次数可以减小VC维
early stopping的方法也是需要交叉验证的




 浙公网安备 33010602011771号
浙公网安备 33010602011771号