机器学习技法(林轩田)学习笔记:Lecture 9 & Lecture 10

Lecture 9: Decision Tree

Decision Tree Hypothesis

之前介绍的uniform blending和linear blending等，\(G\)中每个假设函数\(g_t\)前的权重都是一个常数\(\alpha_t\)(\(G(x)=\sum_{t=1}^T \alpha_t g_t(x)\))，下面介绍的决策树的假设函数G中，每个\(g_t\)前的权重是关于\(x\)的函数\(q_t(x)\)

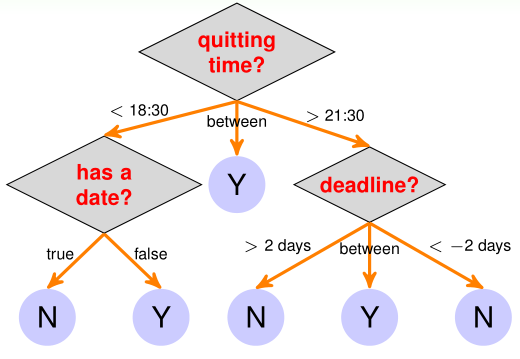
一个决策树如上图所示，可见决策树其实就是模仿人类做决策的判断过程。每个叶节点是一个假设函数\(g_t(x)\)(图中\(g_t(x)\)的取值就是0/1)，对应的权重\(q_t(x)=\) 1{x在根节点到叶节点(\(g_t(x)\))的路径上}，一般决策树的内部结点(非叶结点)都是比较简单的条件

决策树的假设函数\(G(x)\)的形式如下：

从递归的角度看，决策树的假设函数\(G(x)\)还可以定义为：

\[G(x)=\sum_{c\ is\ x's\ son}1\{b(x)=c\}G_c(x) \]

\(1\{b(x)=c\}\)这个权重就是用来根据条件b判断向哪个子树走

决策树的优点：

• 假设函数G具有可解释性，是人类可以理解的。
• 容易实现
• 训练、预测非常高效

决策树的缺点

• 缺乏足够的理论支持
• 新手很难选取合适的树结构
• 没有具有代表性的算法

Decision Tree Algorithm

根据决策树的假设函数\(G(x)\)的递归定义

\[G(x)=\sum_{c\ is\ x's\ son}1\{b(x)=c\}G_c(x) \]

我们可以写出决策树的伪代码：

function DecisionTree(训练集\(\mathcal D=\{(x_n,y_n)\}_{n=1}^N\))

• 如果\(\mathcal D\)达到终止条件:
• ____返回基假设函数\(g_t(x)\)
• 否则:
• ____学习分枝条件\(b(x)\)
• ____根据\(b(x)\)将\(\mathcal D\)分成C个子集\(\mathcal D_c\)
• ____对C个子集\(\mathcal D_c\)建立C个子树$G_c\gets \(DecisionTree(\)\mathcal D_c$)
• 返回\(G(x)=\sum_{c\ is\ x's\ son}1\{b(x)=c\}G_c(x)\)

C&RT决策树

下面介绍一种用于分类和回归的决策树：C&RT(Classification and Regression Tree)，其参数：

• C=2(C&RT是二叉树)
• 基假设函数\(g_t(x)\)是常数，为了满足\(E_{in}\)尽可能小：
• • 对于二分类/多分类问题，\(g_t(x)=\)该叶节点对应的训练样本中占多数的标签\(y_n\)
• • 对于平方误差的回归问题，\(g_t(x)=\)该叶节点对应的训练样本的\(y_n\)的平均值

C&RT的分枝条件学习

在C&RT中，每个内部结点的条件b(x)就是一个decision stump函数\(h(x)\)，它把当前子树对应的训练样本\(\mathcal D\)分成两部分\(\mathcal D_1,\mathcal D_2\)，使得这两部分各自的不纯度(impurity)之和最小，即：

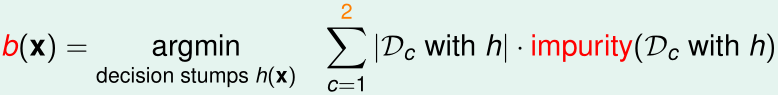
根据回归/分类问题的原始的\(E_{in}\)，我们可以推出它们对应的impurity函数：

对于分类问题，我们还有两种不同的impurity函数：

在分类问题的C&RT中最常用的impurity是Gini index，而在回归问题的C&RT中最常用的impurity是均方误差

C&RT的递归终止条件

在以下两种情况下，C&RT的递归终止：

• 1、当前的所有训练样本的\(y_n\)完全相同(impurity=0)，此时返回\(g_t=y_n\)
• 2、当前的所有训练样本的\(x_n\)完全相同(样本点重叠了)，decision stump没办法"下刀"

为方便描述，我们称以上构造出的C&RT是fully-grown tree

Decision Tree Heuristics in C&RT

Regularization by Pruning

之前介绍的fully-grown tree的C&RT，当所有\(x_n\)都不同时，可以保证\(E_{in}(G)=0\)

但是由于当递归到很深的层(很深的树结点)时，对应的训练集\(\mathcal D\)会很小，此时\(E_{out},E_{in}\)的gap很大，也就很容易发生过拟合了

为了解决这个问题，我们需要对C&RT引入正则化，正则化项\(\Omega(G)=\)G的叶结点数

那么我们希望得到的决策树G应该是：

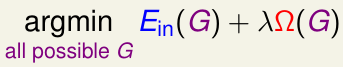
加入正则化后的C&RT被称为pruned decision tree(被修剪过的决策树)

显然我们是无法枚举所有的\(G\)的，一种比较好的近似方法是：

• \(G^{(0)}=\)fully-grown gree
• \(G^{(i)}=\arg\min_GE_{in}\)(从\(G^{(i-1)}\)移掉一个叶节点后得到的树G)

选取正则化项的系数\(\lambda\)的过程也是模型选择过程，需要采用交叉验证的方法

Branching on Categorical Features

之前我们接触过的输入特征都是数值特征(numerical features)，即输入的每一维特征都是实数，那么如果输入的某一维特征是分类特征(categorical feature)，如\(x_i\in\) {fever, pain, tired, sweaty}，该怎么办呢？

此时C&RT每个内部结点的条件\(b(x)\)相应地变成了：

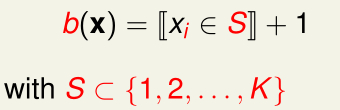
(即，输入的第i个特征(分类特征)\(\in S\)就走第二个子树，否则走第一个子树)

Missing Features by Surrogate Branch

在实际场景中，往往输入特征中某些维度是缺失的，其他学习算法是无法解决这类缺失特征的问题的，而决策树却可以通过surrogate branch解决这类问题。

surrogate branch就是用其他内部结点的分枝条件代替缺失特征的内部结点的条件，比如当前内部结点的分枝条件是{"体重"<=50kg}，我们可以用另一个内部结点的分枝条件：{"身高"<=阈值} 来代替{"体重"<=50kg}

我们在训练决策树时，需要维护与每个条件\(b(x)\)最相似的备用条件\(b'(x)\)，当\(b(x)\)作判断时需要的那一维特征缺失时，就用备用条件\(b'(x)\)替换

总结

C&RT有以下优点：

• 1、假设函数G是人类可以理解的
• 2、可以轻松实现多分类
• 3、可以轻松实现输入categorical feature
• 4、可以轻松解决缺失某些维度特征的情况
• 5、对非线性问题的训练和预测非常高效

Lecture 10: Random Forest

Random Forest Algorithm

Recall: Bagging and Decision Tree

首先回顾一下bagging和决策树：

• bagging通过从\(\mathcal D\) re-sample采样来得到T个\(\tilde{\mathcal D_t}\)，并分别用每个\(\tilde{\mathcal D_t}\)作训练集，使用相同的学习算法\(\mathcal A\)训练出假设函数\(g_t\)，最终通过对T个\(g_t\)的uniform blending获得G，bagging通过结合T个\(g_t\)，可以减小G的方差
• 决策树，特别是fully-grown tree，非常容易过拟合(方差大)

随机森林的motivation就是在保留决策树的一系列优点的前提下，通过bagging的方法减小它的方差

Random Forest (RF)

随机森林，其实就是套用bagging算法，其中bagging的学习算法\(\mathcal A\)就是决策树算法，另外bootstraping的过程也有变化

function Random Forest(\(\mathcal D\))

• For t=1,...,T:
• • (1)通过bootstraping获得大小为N'的训练集\(\tilde{\mathcal D_t}\)
• • (2)使用决策树算法，用训练集\(\tilde{\mathcal D_t}\)训练出\(g_t\)
• 最终得到的G=T个\(g_t\)的uniform blending

其中，bootstrap过程可以是通过原始的\(\mathcal D\) re-sample N'次得到，为了让\(g_t\)更具有多样性，还有另外一种方法：

假设原始的输入特征是d维的，我们选取其中的d'个维度(第\(i_1,\cdots,i_{d'}\)维,\(d'\ll d\))，通过某种随机的线性变换\(\Phi(x)=Px\)映射为新的低维特征(其中\(P\)是\(d'\times d\)列，除第\(i_1,\cdots,i_{d'}\)列外，其他列都是零)

除此以外，为了让\(g_t\)更具有多样性，C&RT的作者建议在每次获得决策树内部结点的分枝条件\(b(x)\)时，都使用一个新的随机\(\Phi(x)\)

Out-Of-Bag Estimate

我们来看bagging(包括随机森林)，T个\(g_t\)使用训练样本的情况：

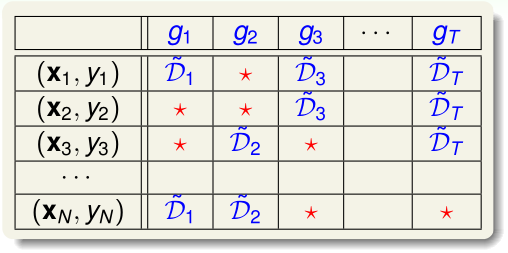
其中红星表明这个样本在\(g_t\)中没有用上

out-of-bag estimate(OOB)的思想就是，用这些标了红星的样本充当验证集。单个\(g_t\)的\(E_{out}(g_t)\)很大，用交叉验证来近似估计它是没有意义的，OOB希望通过交叉验证来估计\(E_{out}(G)\)

我们令\(G_n^-\)=去掉那些训练时用了\((x_n,y_n)\)的\(g_t\)，剩下的\(g_t\)通过uniform blending得到的G，则OOB误差：

\[E_{oob}(G)=\frac 1 N \sum_{n=1}^N err(y_n,G_n^-(x_n)) \]

对于每个\(g_t\)，其\(\tilde{\mathcal D_t}\)中没有包含的(out-of-bag)训练样本的个数有多少呢？假设bootstrap中re-sample是N'=N次，那么对于特定的一个样本\((x_n,y_n)\)，其不在\(\tilde{\mathcal D_t}\)内的概率是

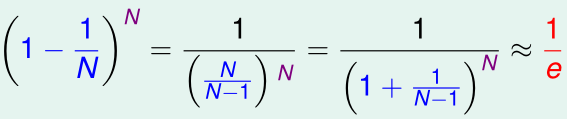
N很大时，该概率趋于1/e，此时对于每个\(g_t\)，其out-of-bag的样本数就是N/e

OOB与一般的交叉验证相比，不需要重新训练每个\(g_t\)，而且一般\(E_{oob}\)对\(E_{out}\)的近似估计很准确

Feature Selection

在特征选择问题中，我们希望移掉那些冗余(重复)特征、与学习问题不相关的特征，当原始特征维数N太大时，我们需要用更高效的方法选取特征，下面介绍基于随机森林的排列测试(permutation test)

如果第i维特征是我们需要的特征的话，假设所有\(x_i^{(n)}\sim P\)，那么我们对每个训练样本，用随机的\(x_i'^{(n)}\sim P\)代替原始的\(x_i^{(n)}\)，学习算法的效果就会变得很差

而分布\(P\)是我们未知的，一种很好的近似方法是对N个样本的第i维特征\(x_i^{(n)}\) random shuffle(这就是这种方法叫permutation test的原因)，这样，random shuffle后仍有：每个\(x_i'^{(n)}\sim P\)

那么第i维特征的重要度importance可以表示为

\(performance(\mathcal D)=E_{oob}(G\ on\ \mathcal D)\),\(performance(\mathcal D^{(p)})=E_{oob}(G\ on\ \mathcal D^{(p)})\)

然而这样的话，在计算\(E_{oob}(G\ on\ \mathcal D^{(p)})\)要重新训练G，为了避免重新训练，我们再做一次近似：用将N个样本第i维\(x_i^{(n)}\) random shuffle后的\(\mathcal D^{(p)}\)对原来的G做OOB验证得到\(E_{oob}^{(p)}(G)\)