机器学习技法(林轩田)学习笔记:Lecture 7 & Lecture 8

Lecture 7:Blending and Bagging

Motivation of Aggregation

现在给出T个假设函数\(g_1,\cdots,g_T\)，我们希望充分利用它们，得到一个更好的假设函数\(G\)，我们有几种方法：

• 1、用交叉验证的方法从T个g里选\(E_{val}\)最小的：\(G(x)=g_{t^*}(x),t^*=\arg\min_{t}E_{val}(g_t^-)\)
• 2、均匀混合T个假设函数的输出结果。例如在二分类问题中，G输出T个假设函数的占多数的输出结果
• 3、将T个假设函数的输出结果加权输出
• 4、将T个假设函数的输出结果加权输出，但每个权重是关于输入x的函数\(q_t(x)\)

其中，第一种方法需要保证\(\min_{t}E_{val}(g_t^-)\)很小，才能保证很好的学习结果。但集成学习并不需要这个保证，它可以从很多个弱的假设函数g结合出更强的假设函数G

例如上图这个例子，假设现在已有三个弱假设函数(图中平行于坐标轴的三条灰线)，通过集成学习可以得到更强的G(图中黑线)，实现二分类。

Uniform Blending

Uniform Blending中，每个假设函数的权重都是1，例如在二分类中：

\[G(x)=\mathrm{sign}(\sum_{t=1}^T 1\cdot g_t(x)) \]

在多分类问题中，就是

\[G(x)=\arg\max_{1\leq k\leq K}\sum_{t=1}^T 1\{ g_t(x)=k\} \]

在回归问题中，就是

\[G(x)=\frac 1 T \sum_{t=1}^T g_t(x) \]

当T个g完全相同时，G就等同于单个g了，G的效果没有提升；但当T个g的差异很大时，通过uniform blending得到的G的效果会显著提升

在回归问题中，

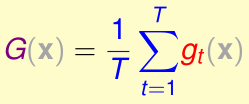
对于给定的单个输入x，

所以

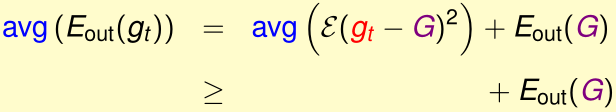
(其中\(\varepsilon(g_t-G)^2\)表示\((g_t-G)^2\)在输入$x\sim \(某种概率分布\)P$的期望)

这个不等式解释了G的泛化误差比较小的原因

再考虑一个特殊的情况：T个线性回归的假设函数\(g_1,\cdots,g_T\)都是通过根据同一个概率分布，独立地随机采集N个样本得到训练集\(\mathcal D_t\)，然后用相同的学习算法\(\mathcal A\)训练得到的，即\(g_t=\mathcal A(\mathcal D_t)\)

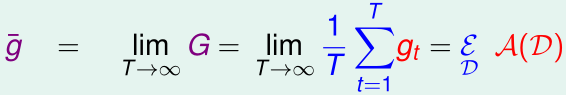
根据之前推出的不等式，可得：

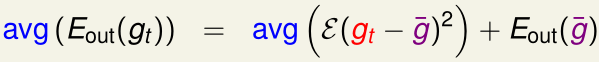
等式右边第一项\(avg(\varepsilon(\cdots))\)被称为方差，表示不同训练集\(\mathcal D_t\)训练出的\(g_t\)之间的差距有多少；

第二项\(E_{oug}(\bar g)\)被称为偏差

Linear Blending

linear blending就是把所有的g的输出结果加权，例如在线性回归问题中，

\[G(x)=\sum_{t=1}^T \alpha_tg_t(x) \]

为了求出参数\(\alpha\)，我们需要最优化：

注意参数\(\alpha_t\)不需要限制条件\(\alpha_t\geq 0\)，因为\(\alpha_t<0\)时，让\(g_t(x)\)取反就相当于\(\alpha_t> 0\)了

类似模型选择，这里我们也要把\(\mathcal D\)分成训练集\(\mathcal D_{train}\)、验证集\(\mathcal D_{val}\)，用\(\mathcal D_{train}\)训练得到\(g_t^-,\alpha_t\)，然后再用整个\(\mathcal D\)对每个\(g_t\)进行训练，最终得到的\(\mathcal D_{train}\)是系数为\(\alpha_t\)，对\(g_t\)而非\(g_t^-\)的线性组合

除了linear blending外，G还可以是关于\(g_t\)的更高阶形式的非线性函数，这种被称为any blending(stacking)，其优点是模型复杂度提高，缺点是更容易带来过拟合

Bagging(Bootstrap Aggregation)

之前的uniform blending和linear blending都是根据已有的T个假设函数\(g_t\)，结合成新的G，但是我们该如何产生不同的\(g_t\)呢？

首先回顾之前的偏置、方差公式：

这里我们做两个近似：

• 1、T不再是正无穷大，而是有限值
• 2、每个\(g_t\)的训练集\(\mathcal D_t\)中的每个样本，都服从相同的概率分布P(且是独立同分布)，而现在我们用已有的\(\mathcal D\)构造近似的\(\mathcal D_t\)

为了实现第二点，我们采用bootstraping，假设当前有N个训练样本\(\mathcal D\)，我们从中随机抽一个样本，再放回去，如此重复N'次(N'不一定要等于N)，这样就能构造大小为N'的\(\mathcal D_t\)

用bootstraping构造T个训练集\(\mathcal D_t\)，训练出T个假设函数\(g_t\)，然后aggregate的方法叫bagging。

需要注意的是，只有当学习算法对数据的样本分布很敏感时，bagging才有较好的表现

Lecture 8: Adaptive Boosting

Motivation of Boosting

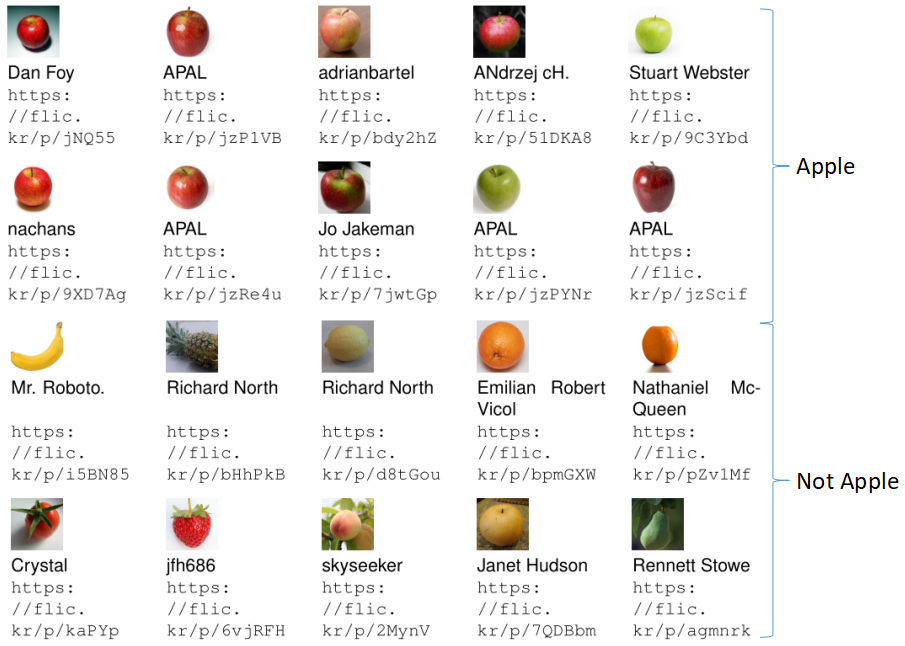
我们举例来说明adaboost的学习流程：如上图所示，现在给出若干图片作训练集，训练一个算法，让它可以判断输入的图片是否是苹果。初始时，每个训练样本的权重相同

第一轮：我们认为圆的物体是苹果，结果一些样本分类错误(上图中蓝色)，我们把这些犯错的样本的权重变大，把分类正确的样本的权重减小

第二轮：为了让每个样本上的错误值的加权减小，我们想出了新的分类方法：红色的物体是苹果。结果这次又有一些样本分类错误(上图中蓝色)，同样地，我们把这些犯错的样本的权重变大，把分类正确的样本的权重减小

第三轮：为了让每个样本上的错误值的加权减小，我们想出了新的分类方法：绿色的物体是苹果。结果这次又有一些样本分类错误(上图中蓝色)，同样地，我们把这些犯错的样本的权重变大，把分类正确的样本的权重减小

这样，我们从这三轮过程中得到了一种分类方法：大多数圆的物体是苹果，苹果大多数情况下是红色的，少数情况下是绿色的

Diversity by Re-weighting

在bootstrap里，我们每一次从\(\mathcal D\)通过re-sample的方式随机采样获得\(\tilde {\mathcal D_t}\)的过程，可以看作是给原始的\(\mathcal D\)中每个样本加上一个权重

例如下图中，我们从\(\mathcal D\) re-sample采样得到\(\tilde {\mathcal D_t}\)

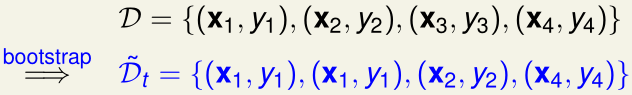
这个过程相当于给原始的\(\mathcal D\)中每个样本加上了权重\(u_i\)：

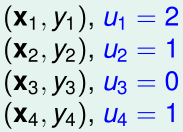
同时，误差函数也变成单点误差的加权之和：

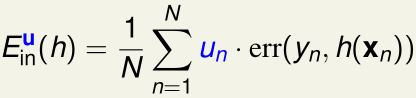
\(\mathcal D\)上这个新的误差函数，与\(\tilde {\mathcal D_t}\)上的误差函数，是完全一样的

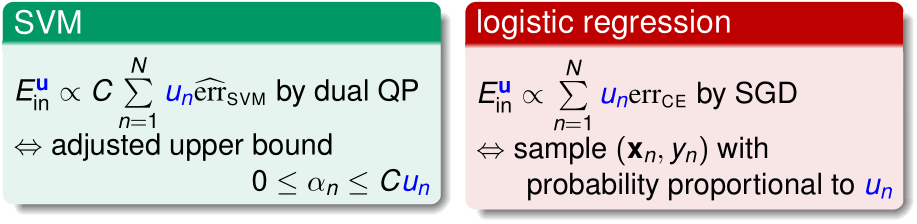
在Soft-margin SVM中，只需要把优化目标中单点误差\(\xi_n\)前乘上\(u_n\)即可，变成\(C\sum_{n=1}^Nu_n\xi_n\)

在逻辑回归中，我们把第n个样本复制\(u_n\)次，从而使它在SGD中被抽中的概率放大\(u_n\)倍即可

在二分类问题中，假设我们现在已经有N个\(u_n^{(t)}\)了，我们可以得到假设函数

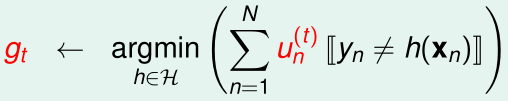
现在我们希望从\(g_t\)，N个\(u_n^{(t)}\)通过调整权重u，得到N个\(u_n^{(t+1)}\)，从而得到下一个不同的\(g_{t+1}\)

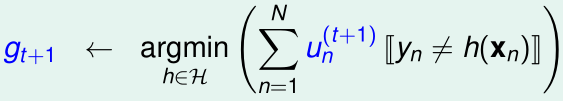
为了让\(g_{t+1}\)与\(g_{t}\)不同，我们希望\(g_{t}\)在加权为\(u_n^{(t+1)}\)的表现尽可能差，从而保证\(g_{t+1}\neq g_{t}\)

\(g_{t}\)在加权为\(u_n^{(t+1)}\)的表现最差时，近似于完全瞎猜，加权错误率为1/2，于是我们希望构造出\(u_n^{(t+1)}\)，满足：

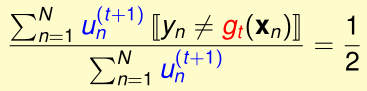
最简单的办法就是，设\(\epsilon_t=\)第t轮的加权错误率

所有分类正确的，\(u_n\)乘上\(\epsilon_t\)；分类不正确的，\(u_n\)乘上\(1-\epsilon_t\)

Adaptive Boosting Algorithm

我们定义缩放因子\(\blacklozenge_t=\sqrt{\frac{1-\epsilon_t}{\epsilon_t}}\)

对于所有分类正确的，\(u_n\)除以\(\blacklozenge_t\)；分类不正确的，\(u_n\)乘上\(\blacklozenge_t\)

这样处理\(u_n\)后，一样可以实现

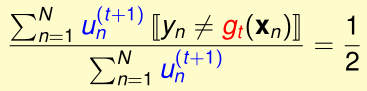
当\(\epsilon_t<\frac 1 2\)，表明\(\blacklozenge_t>1\)，这样就相当于是放大那些分类错误的样本，缩小那些分类正确的样本了

现在我们可以得到一个初步的算法了：

• 初始化：所有的\(u_n^{(1)}=\frac 1 n\)
• for t=1...T{
• ____(1)根据\(\mathcal A(\mathcal D,u^{(t)})\)获得\(u^{(t)}\)加权的错误率最小的\(g_t\)
• ____(2)用缩放因子\(\blacklozenge_t=\sqrt{\frac{1-\epsilon_t}{\epsilon_t}}\)，从\(u^{(t)}_n\)更新到\(u^{(t+1)}_n\)
• }

现在还剩一个问题，最终T个\(g_t\)该怎么结合成\(G(x)\)？adaptive boosting算法可以在求解\(g_t\)的过程中解决这个问题：

• 初始化：所有的\(u_n^{(1)}=\frac 1 n\)
• for t=1...T{
• ____(1)根据\(\mathcal A(\mathcal D,u^{(t)})\)获得\(u^{(t)}\)加权的错误率最小的\(g_t\)
• ____(2)用缩放因子\(\blacklozenge_t=\sqrt{\frac{1-\epsilon_t}{\epsilon_t}}\)，从\(u^{(t)}_n\)更新到\(u^{(t+1)}_n\)
• ____(3)计算\(\alpha_t=\ln(\blacklozenge_t)\)
• }
• 最终的\(G(x)=\mathrm{sign}(\sum_{t=1}^T\alpha_tg_t(x))\)

对于\(g_t\)而言：

• 最坏情况下，其加权错误率为1/2，此时的\(\blacklozenge_t=1,\alpha_t=0\)，相当于它在最终决策时不作任何贡献
• 最好情况下，其加权错误率为0，此时的\(\blacklozenge_t=+\infty,\alpha_t=+\infty\)，相当于它在最终决策时起无穷大的作用
• 其加权错误率越低，\(\alpha_t\)越大，它在最终决策时起的作用也就越大

下面不加证明地给出adaboost算法的VC Bound：

不等式右侧的第一项\(E_{in}(G)\)，当满足\(\epsilon _t\leq \epsilon <\frac 1 2\)时，可以保证在迭代次数\(T=O(log N)\)时可以实现\(E_{in}(G)=0\)

不等式右侧的第二项,随T增大时增长很缓慢，而N足够大时，就能保证这一项很小了

所以当基算法\(\mathcal A\)满足\(\epsilon _t\leq \epsilon <\frac 1 2\)时(保证比乱猜要强)，哪怕基算法很弱，通过Adaboost也可以保证\(E_{in}=0,E_{out}\)很小

总结：Adaboost基于弱的基算法\(\mathcal A\)，通过\(\blacklozenge_t\)调整加权错误率的权重，使用\(\alpha\)组合T个弱的假设函数\(g_t\)，可以得到很强的假设函数G

Adaptive Boosting in Action

实际的adaboost最常用的基函数为decision stump：

该假设函数有三个参数\(s\in\{1,-1\},i,\theta\)，表示选取输入x的第i个特征\(x_i\)，当\(x_i\geq \theta\)时输出s，否则输出-s，如果输入特征是二维的，在二维平面上看，这个函数的决策边界就是一条与坐标轴平行的直线

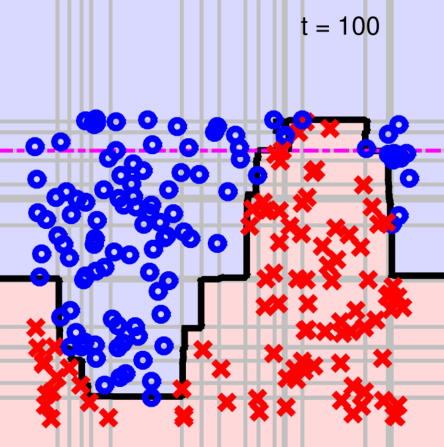
最终adaboost得到的决策边界(图中黑色)就是由若干个decision stump(图中灰色)构成的