机器学习技法(林轩田)学习笔记:Lecture 1 & Lecture 2
Lecture 1:Linear Support Vector Machine
Large-Margin Separating Hyperplane
在二分类问题中,假设现在我们有大小为n的线性可分的训练集\(\mathcal D\)
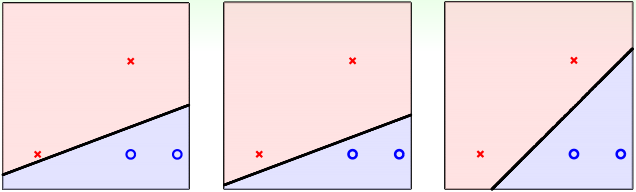
在PLA/口袋算法中,对于上图中的三种假设函数\(h=\mathrm{sign}(w^Tx)\)而言,哪一种是最好的呢?
实际上这三种假设函数对于PLA/口袋算法而言是一样好的,因为它们都满足\(E_{in}(h)=0\),在这个训练集上跑PLA,这三种假设函数最终都有可能得到
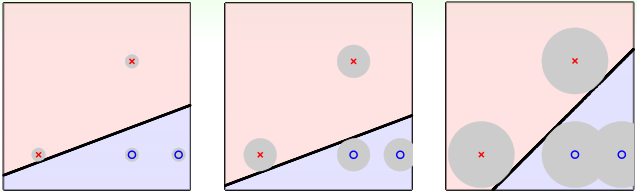
但是如果我们把测试数据的x看作是某个训练样本的\(x^{(i)}\)加上噪声的结果,即测试数据的x在某个训练样本的\(x^{(i)}\)附近(以\(x^{(i)}\)为中心的圆区域内),那么我们希望最终得到的决策边界距离每个训练样本的\(x^{(i)}\)越远越好,这样才能让假设函数对测试数据的噪声(偏差)的容忍度(即上图灰色圆区域半径)尽可能大,因此,我们最希望得到的假设函数应该是上图的第三个。

我们把距离决策边界最近的训练样本的\(x^{(i)}\)到边界的距离称为margin,那么我们希望得到margin最大,且\(E_{in}=0\)(即所有的\(y^{(i)}w^Tx^{(i)}>0\))的假设函数,优化目标可以表示为:
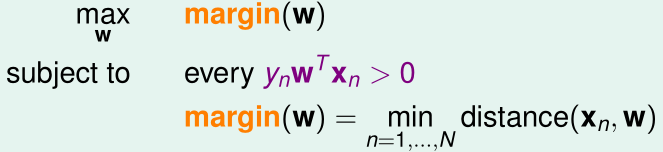
Standard Large-Margin Problem
首先我们约定,后面涉及的向量\(w=(w_1,\cdots,w_d)^T,x=(x_1,\cdots,x_d)^T\),不再额外补充偏置项\(w_0=b,x_0=1\),那么假设函数可以表示为:
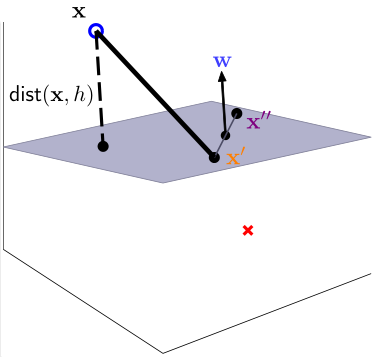
那么每个训练样本\(x\)到决策边界\(w^Tx+b\)的距离是多少呢?
首先证明\(w\)是决策边界(超平面)\(w^Tx+b\)的法向量。对于任意的决策边界上的点\(x',x''\),都有\(w^Tx'+b=0,w^Tx''+b=0\),两式相减得\(w^T(x''-x')=0\),这表明\(w\)垂直于决策边界,是它的法向量
那么训练样本\(x\)到决策边界\(w^Tx+b\)的距离\(dist(x,h)\)就是向量\(x-x'\)到法向量w的投影的大小:
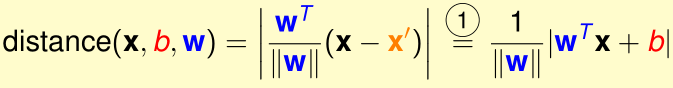
为了去掉绝对值,\(w^Tx^{(i)}+b\)外面乘上\(y^{(i)}\):
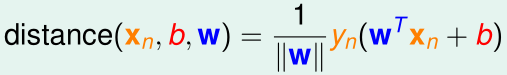
那么我们的优化目标可以写为:
其中,\(margin(b,w)=\min_i\frac 1 {\|w\|}y^{(i)}(w^Tx^{(i)}+b)\)
我们发现,如果找到了一组满足条件的\((b,w)\),那么\((kb,kw)\)也能满足条件,而且二者对应的是完全相同的决策边界。为了解决这个问题,我们可以加上限制:\(\min_i y^{(i)}(w^Tx^{(i)}+b)=1\)
此时,优化目标等同于:
其中,\(margin(b,w)=\min_i\frac 1 {\|w\|}y^{(i)}(w^Tx^{(i)}+b)=\frac 1 {\|w\|}\)
有了第二项约束条件后,第一项约束条件(\(y^{(i)}w^Tx^{(i)}>0\))就是多余的了,可以省去,再把\(margin(b,w)=\frac 1 {\|w\|}\)代进优化目标:
这里的约束条件\(\min_i y^{(i)}(w^Tx^{(i)}+b)=1\)等价于\(\min_i y^{(i)}(w^Tx^{(i)}+b)\geq 1\):
- 首先,\(\min_i y^{(i)}(w^Tx^{(i)}+b)=1\)显然可以推出\(\min_i y^{(i)}(w^Tx^{(i)}+b)\geq 1\)
- 然后用反证法证明:\(\min_i y^{(i)}(w^Tx^{(i)}+b)\geq 1\)可以推出\(\min_i y^{(i)}(w^Tx^{(i)}+b)=1\)
假设约束条件为\(\min_i y^{(i)}(w^Tx^{(i)}+b)\geq 1\)时,找到的最优解\((b^*,w^*)\)满足 \(\min_i y^{(i)}(w^{*T}x^{(i)}+b^*)\geq k>1\),最优值为\(\frac 1 {\|w^*\|}\)
那么我们完全可以找出决策边界一模一样的\((\frac{b^*}{k},\frac{w^*}{k})\),满足 \(\min_i y^{(i)}((\frac{w^*}{k})^Tx^{(i)}+\frac{b^*}{k})\geq 1\),而它的最优值为\(\frac k {\|w^*\|}>\frac 1 {\|w^*\|}\),与假设矛盾
所以,最优解\((b^*,w^*)\)一定满足 \(\min_i y^{(i)}(w^{*T}x^{(i)}+b^*)=1\)
所以优化目标等价于
因为最大化\(\frac 1 {\|w\|}\)等价于最小化\(\|w\|\),等价于最小化\(\frac 1 2 \|w\|^2=\frac 1 2 w^Tw\),优化目标进一步等价于
Support Vector Machine
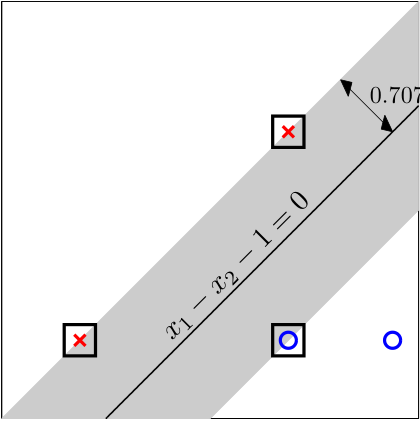
我们称距离最优决策边界最近的那些样本\(x^{(i)}\)(\(dist(x^{(i)},h)=margin\))叫作支持向量(support vector),这就解释了支持向量机的名称的由来。
这个优化问题是一个二次规划问题(Quadratic programming,QP),一般的二次规划问题形式如下:

我们令该问题中每个变量取值分别为:
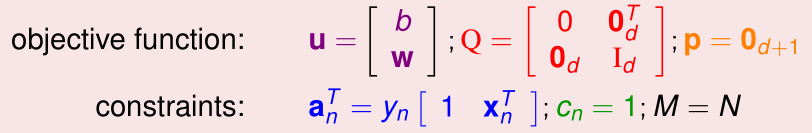
这样就能把SVM的优化问题转化成二次规划问题了,二次规划问题可以直接用现有的工具包优化求解。
现在我们介绍的SVM被称为linear hard-margin SVM
Reasons behind Large-Margin Hyperplane
为什么SVM比之前介绍的PLA算法效果更好呢?

在之前的机器学习基石里介绍过正则化,正则化相当于是在加上\(w^Tw\leq C\)的约束条件下最小化\(E_{in}\),而这里SVM则是在要求\(E_{in}=0\)(不仅如此,还要求\(y^{(i)}w^Tx^{(i)}\geq 1\))的前提下最小化\(w^Tw\),也可以视为一种"weight-decay"的正则化
另外一方面,在给定数据点\(x^{(1)},\cdots,x^{(n)}\)的前提下,SVM的\(|\mathcal H|\)
Lecture 2:Dual Support Vector Machine
Motivation of Dual SVM
在原始的hard-margin SVM的优化问题中,如果我们希望决策边界不是线性的,就需要通过特征变换\(\Phi\)将原始\(d+1\)维特征\(x\)变成更高阶的\(\tilde d+1\)维新特征\(z=\Phi(x)\),此时优化目标变成:
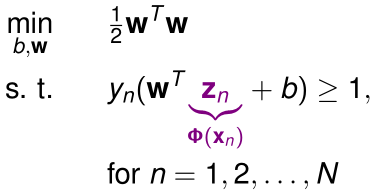
如果\(\tilde d\)太大(甚至是无穷大),那么最优化参数就会很困难
现在我们的目标是让SVM的优化过程尽量减小对\(\tilde d\)的依赖
首先,我们可以构造广义拉格朗日函数(其中\(\alpha_n\)是拉格朗日乘子,\(\alpha_n\geq 0\)):
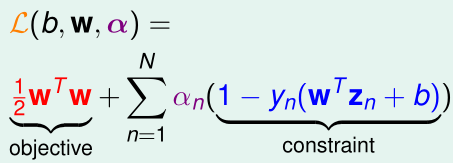
原始优化问题就相当于:
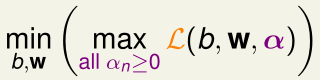
当\(b,w\)不满足原始的约束条件时,存在\((1-y_n(w^Tz_n+b))>0\),取\(\alpha_n=+\infty\),此时\(\max_{all\ \alpha_n\geq 0}\mathcal L=+\infty\)
而\(b,w\)满足原始的约束条件时,所有的\((1-y_n(w^Tz_n+b))\leq 0\),此时要最大化\(\mathcal L\),就要让所有的\(\alpha_n(1-y_n(w^Tz_n+b))= 0\),此时\(\max_{all\ \alpha_n\geq 0}\mathcal L=\frac 1 2 w^Tw\)
此时\(\min_{b,w}\max_{all\ \alpha_n\geq 0}\mathcal L\)肯定不是\(+\infty\),也就相当于是排除掉所有不符合原始约束条件的\(w\)了,而求出的最优解也就是原始的SVM优化问题的最优解
Lagrange Dual SVM
回顾上一节广义拉格朗日乘数法的优化问题:
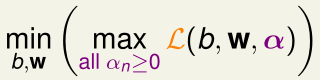
其中,对于固定的\(\alpha'\)(其中所有\(\alpha_n'\geq 0\)),显然:
所以有:
该等式对任何符合条件的固定的\(\alpha'\)都成立,所以不等式右侧可以加上\(\max_{all\ \alpha_n'\geq 0}\)
不等式左边的优化问题是拉格朗日原始问题,右边的优化问题被称为拉格朗日对偶问题
当不等式取等时,我们称之为强对偶,强对偶的条件为:
- 拉格朗日原始问题为凸函数
- 拉格朗日原始问题有最优解(当\(z^{(1)},\cdots,z^{(n)}\)线性可分时成立)
- 所有约束条件都是线性的
下面我们来最优化拉格朗日对偶问题\(\max_{all\ \alpha_n'\geq 0}\min_{b,w}\mathcal L(b,w,\alpha')\)
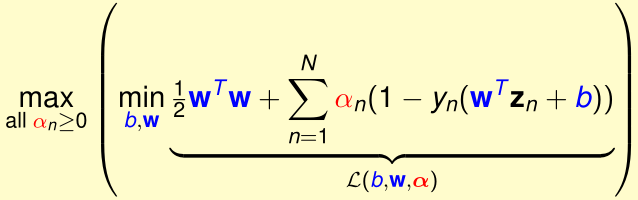
首先要确定内层min(...)的值,内层min(...)取极小值时,\(\mathcal L\)对b,向量\(w\)的导数都为0
我们令\(\mathcal L\)对\(b\)求导:
再令\(\mathcal L\)对向量\(w\)求导:
得满足内层min(...)取得最小值时,应有
这两个可以当作外层max的约束条件,然后把这两个约束条件代入内层min里的\(\mathcal L\),得:
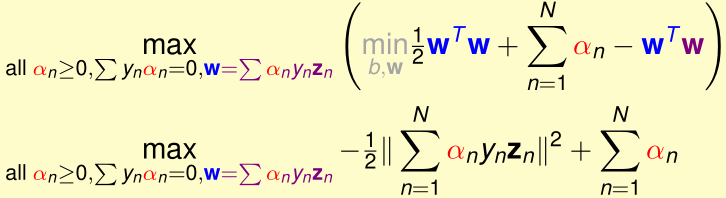
前人已经证明,当满足KKT条件时,拉格朗日对偶问题的最优解\((b,w,\alpha)\)也就是拉格朗日原始问题的最优解,KKT条件为:
- (1)拉格朗日原始问题有解:原始问题的解w要满足:所有的\(y_n(w^Tz_n+b)\geq 1\)
- (2)拉格朗日对偶问题有解:拉格朗日对偶问题的解\(\alpha\)要满足所有\(\alpha_n\geq 0\)
- (3)对偶问题的内层必须取得最小值:\(\sum_{n=1}^N \alpha_ny_n=0\),\(w=\sum_{n=1}^N\alpha_ny_nz_n\)
- (4)原始问题的内层必须取得最小值,之前说过,取得最小值时拉格朗日项为0:\(\alpha_n(1-y_n(w^Tz_n+b))=0\)
可以证明,KKT条件,是拉格朗日对偶问题的最优解\((b,w,\alpha)\)等同于拉格朗日原始问题的最优解,的充要条件
Solving Dual SVM
我们可以通过求拉格朗日对偶问题的最优解\(\alpha\)来获得最优的\(b,w\)
回顾一下这个拉格朗日对偶问题:
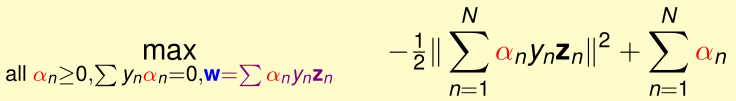
展开max(...)内的部分,这个问题相当于一个带约束条件的二次规划问题:
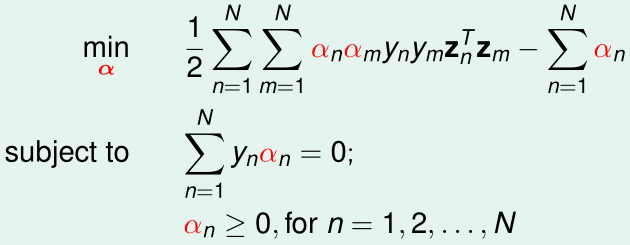
该最优化问题有n个变量(\(\alpha_1,\cdots,\alpha_n\)),n+1个约束条件(n个不等式约束,1个等式约束)
为了与标准的二次规划问题对应起来,我们把等式约束拆成两个不等式约束:
即
再与QP问题的标准形式对应起来:

求出最优的\(\alpha\)后,根据KKT条件(3)可以得到\(w=\sum_{n=1}^N\alpha_ny_nz_n\)
然后,由KKT条件(4):\(\alpha_n(1-y_n(w^Tz_n+b))=0\)可以发现,当\(\alpha_n>0\)时,有\(y_n(w^Tz_n+b)=1\),即\(w^Tz_n+b=y_n\)(说明\(x_n\)是支持向量),所以我们只要找任意一个\(\alpha_n>0\),即可得到\(b=y_n-w^Tz_n\)
Messages behind Dual SVM
上一节中,我们已经提到过\(\alpha_n>0\)的\(x_n\)都是支持向量,但是要注意\(x_n\)是支持向量并不能得到\(\alpha_n>0\)(KKT条件(4)表明也可以是\(\alpha_n=0\))
我们根据获得最优的\(\alpha\)后推导\(w,b\)的公式,可以看出,\(w,b\)只与\(\alpha_n>0\)的支持向量有关
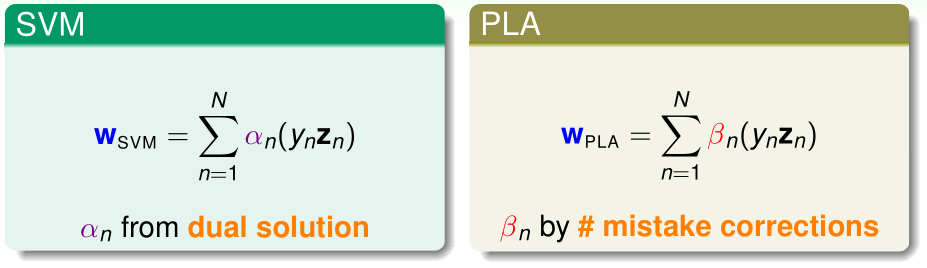
回顾之前学过的PLA,SVM、PLA的\(w\)都可以看作是N个\(y_nz_n\)的加权之和,只不过SVM的\(y_nz_n\)的权重是对偶问题的最优解\(\alpha_n\),而PLA的\(y_nz_n\)的权重是PLA训练过程中在第n个样本上的犯错次数。
对于基于批量梯度下降/随机梯度下降的逻辑回归、线性回归而言,若\(w_0=0\),则它们的w也可以看作是\(y_nz_n\)的线性组合,我们称这样的w能被数据表示
而在SVM中,由于w只是那些\(\alpha_n>0\)的支持向量的\(y_nz_n\)的线性组合,因此我们说SVM的w只被支持向量表示
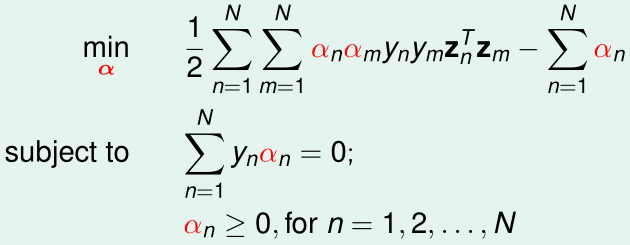
在对偶问题中,\(\tilde{d}\)只存在于\(y_ny_mz_n^Tz_m\)的运算过程中,计算\(y_ny_mz_n^Tz_m\)的复杂度是\(O(\tilde d)\)的,为了避免受到\(\tilde d\)的影响,后面会采用核函数的方法解决此问题
另外由于对偶问题有n个变量,在数据量n很大时,使用一般的二次规划算法是不可行的,因此我们要利用约束条件\(\sum_{n=1}^N y_n\alpha_n\)

