机器学习基石(林轩田)学习笔记:Lecture 16

Lecture 16:Three Learning Principles

Occam's Razor

奥卡姆剃刀原则：如无必要，勿增实体(entities must not be multiplied beyond necessity)

意思就是，拟合训练数据时，在保证\(E_{in}\)足够小的前提下，要用尽可能简单的模型去拟合。

简单的假设函数h的参数比较少，对应的假设函数集\(\mathcal H\)的大小比较小。这两点之间是有关联性的：h的参数如果可以用l个二进制位描述的话，对应的\(|\mathcal H|=2^l\)，也就是说，假设函数h的参数少，等同于\(|\mathcal H|\)小

我们可以从另一角度解释奥卡姆剃刀原则。机器学习算法是希望通过训练数据学习到某种规律，假设现在有\(n\)个点作为n个训练样本的输入特征，我们随机把它们分为正负样本(共有\(2^n\)种标签方法)，那么学习算法训练出的\(g\)，使得\(E_{in}(g)=0\)的概率小于等于\(\frac {m_\mathcal H(n)}{2^n}\)(根据Lecture 5 成长函数\(m_\mathcal H\)的定义，这n个点最多只有\(m_\mathcal H(n)\)种标签方案，能被\(g\in \mathcal H\)完美分类)

\(\mathcal H\)越是复杂时，\(m_\mathcal H(n)\)越大，学习算法能对这堆毫无规律性的训练数据完美分类的概率越高，也就说明越容易过拟合了

Sampling Bias

在Hoffending不等式里，我们有前提条件：采样的样本\(x^{(i)}\)与真实的\(x\)都满足独立同分布，且概率分布都为\(P\)，在满足这一前提时，该不等式才成立。

在VC理论中，训练样本的分布\(P(x^{(i)},y^{(i)})\)要与真实的\(P(x,y)\)足够接近，我们才能保证\(E_{in}(g),E_{out}(g)\)是足够接近的。

因此，在机器学习训练过程中，我们应该让训练样本、验证集样本的分布尽可能接近真实测试环境的样本的分布

Data Snooping

之前本课程提到过，在模型选择时，我们应尽量避免偷窥数据，实际上，在机器学习实践中，我们很容易无形中让测试数据受到污染

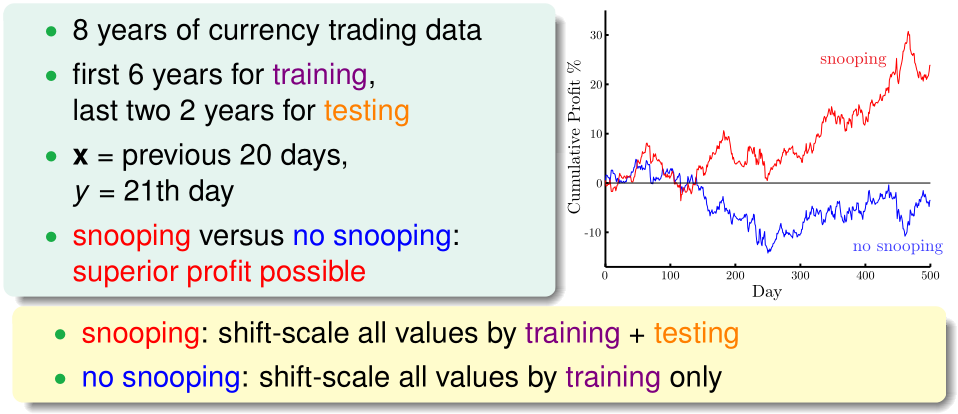
例如在汇率预测问题中，我们选前6年数据作训练数据，后2年数据作测试数据，在对训练数据放缩预处理时，我们用8年的全部数据提供信息，比只用前6年的数据提供信息，结果更好。因为前者相当于无形中偷窥了测试数据。