机器学习基石(林轩田)学习笔记:Lecture 12 & Lecture 13
Lecture 12:Nonlinear Transformation
Quadratic Hypothesis

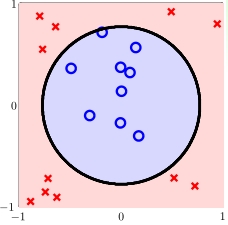
在二分类问题中,如果我们遇到的训练集是上图所示的\(x\in \mathbb R^2\)的若干训练样本,这些样本是线性不可分的,我们只能考虑用更高阶的假设函数,如二次的假设函数\(h(x)=\mathrm{sign}(-x_1^2-x_2^2+0.6)\)
我们可以把这个二次的假设函数里每一项(常数项1、二次项\(x_1^2,x_2^2\))看作是经过某种特征变换\(\Phi\)得到的新特征\(z_i\)
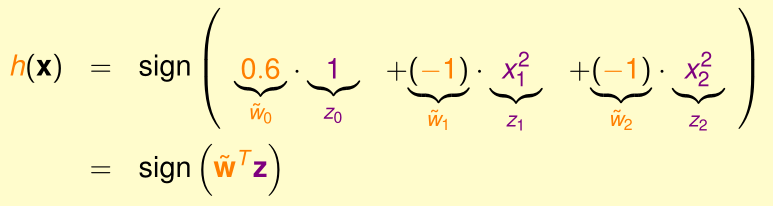
这个特征变换\(\Phi\)可以看作是一个由输入特征空间\(\mathcal X\)映射到\(\mathcal Z\)的函数:\(\Phi:\mathcal X\mapsto \mathcal Z\)
在上图中,训练样本的输入特征在\(\mathcal X\)中是线性不可分的,但是经特征变换\(\Phi\)映射到\(\mathcal Z\)中后就变成线性可分的了。
更一般地,一个从\(x=(x_1,x_2)\)变换到二次特征\(z\)的\(\Phi\)为:
那么对于之前我们已经学过的线性的机器学习算法而言,只要把输入特征经过特征变换映射到二阶形式的新特征,再套用原有的线性的机器学习算法,就变成了二次的机器学习算法。
Nonlinear Transform
类似于从原始一次特征映射到二次特征,实现二次的机器学习算法一样,我们也可以从原始一次特征通过\(\Phi\)映射到更高阶的特征,然后用这些更高阶的特征作为输入特征,训练机器学习算法,之后,对于每个新的输入样本x,用\(\Phi(x)\)作输入特征提供给学习算法,从而得到预测结果。
Price of Linear Transform
假设输入特征是d+1维的,\(x=(1,x_1,\cdots,x_d)\),通过特征变换\(\Phi_Q(x)\)映射到Q阶特征

得到的新的特征的维度为\(1+\tilde d\)=\((1+x_1+\cdots+x_d)^Q\)的展开式的项数=\(C_{Q+d}^Q=C_{Q+d}^d=O(Q^d)\)
(具体证明参考https://wenku.baidu.com/view/ce95c41902d276a201292e3b.html)
可见,随着输入特征维度d与新特征阶数Q的增大,新的特征的维度会爆炸式增长,这将大大提高存储与学习算法训练过程的代价
另一方面,阶数Q很大时,Q阶的假设函数的VC维也会变得很大,不过由于Q阶的假设函数的参数个数为\(\tilde d+1\),根据Lecture 7的推导,任意\(\tilde d+2\)个数据点不能被\(\mathcal H_{\Phi_Q}\) shattered,所以我们可以保证\(d_{VC}(\mathcal H_{\Phi_Q})\leq \tilde d+1\)
Structured Hypothesis Sets
假设输入特征是d+1维的,\(x=(1,x_1,\cdots,x_d)\),通过特征变换\(\Phi_Q(x)\)映射到Q阶特征,我们发现:

设通过\(\Phi_Q\)映射到新的Q阶特征,构建出的Q阶的假设函数的集合为\(\mathcal H_Q\),显然:

由于高阶的假设函数集包含了整个低阶的假设函数集,所以显然高阶的\(\mathcal H\)的\(E_{in}(g)\)比低阶的\(\mathcal H\)的\(E_{in}(g)\)小(g是学习算法找到的\(E_{in}\)最小的假设函数,因为高阶\(\mathcal H\)有更多假设函数可供选择,所以它的\(E_{in}\)更小)
另外,我们还能发现,高阶的\(\mathcal H\)的VC维更高
证明:若高阶的\(\mathcal H_{Q}\)的VC维是\(d_{VC}(\mathcal H_{Q})\)),低阶的\(\mathcal H_{q}\)的VC维是\(d_{VC}(\mathcal H_{q})\)
则存在一组\(d_{VC}(\mathcal H_{q})\)个数据点,可以被\(\mathcal H_q\) shattered,而\(\mathcal H_q\subset \mathcal H_Q\),说明这些点可以被\(\mathcal H_Q\) shattered
因此,\(d_{VC}(\mathcal H_{Q})\geq d_{VC}(\mathcal H_{q})\)
于是我们可以得到:

回顾Lecture 7的学习曲线:
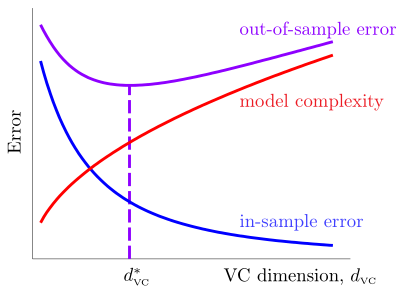
可见,\(E_{out}(g)\)是先减小,后增大的,新特征的阶数(以及VC维)不是越大越好
实践中,我们应该尽量采用低阶的特征:首先尝试使用一阶特征,再采用二阶特征,以此类推,直到\(E_{in}(g)\)达到足够小
Lecture 13:Hazard of Overfitting
What is Overfitting?
回顾Lecture 7的学习曲线:

当\(d_{VC}> d^*_{VC}\)时,随着\(d_{VC}\)增大,\(E_{in}\)不断减小,而\(E_{out}\)不断增大,这时候发生了过拟合。
过拟合发生的原因有:
- VC维过高
- 存在噪声(noise)
- 训练集大小n太小
如果过拟合存在,就会导致学习模型的泛化能力差(bad generalization)
The Role of Noise and Data Size
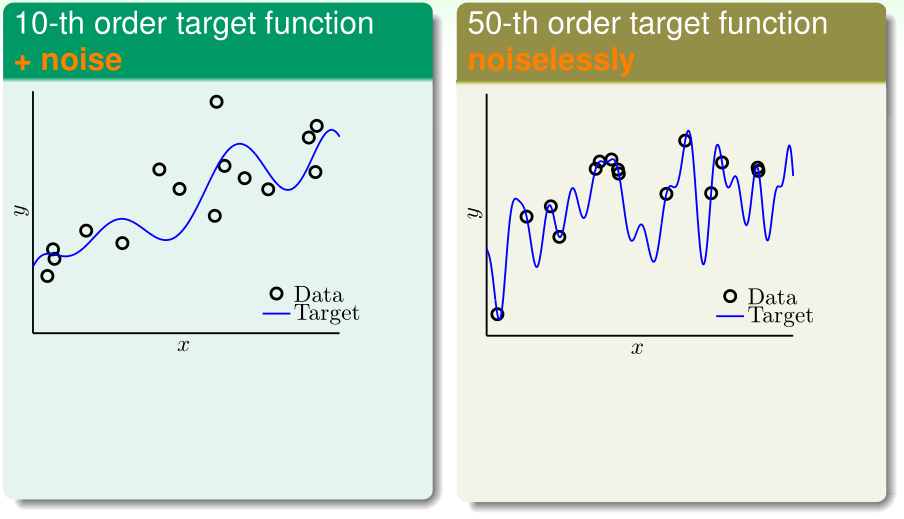
考虑两种情况:
- 左图:理想的目标函数f(x)是10阶的,而从f(x)获得的训练样本噪声很大
- 右图:理想的目标函数f(x)是50阶的,而从f(x)获得的训练样本噪声很小
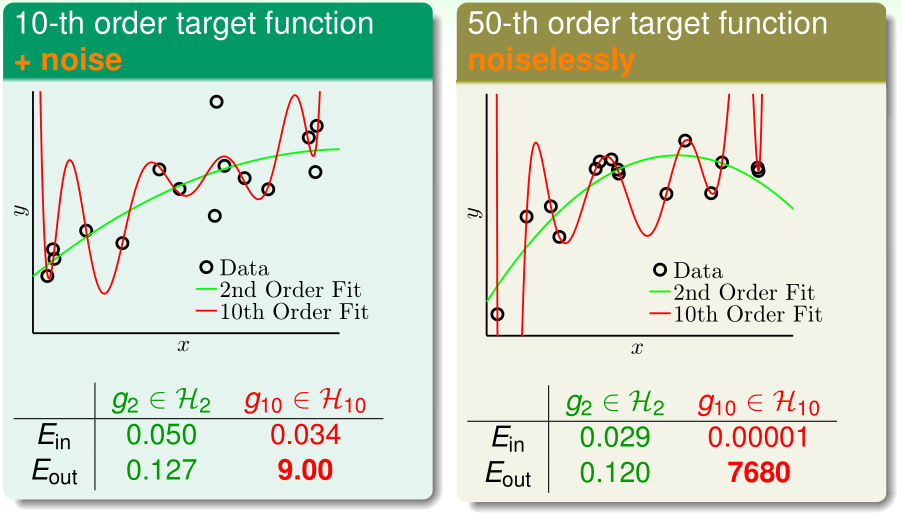
现在我们分别用二次函数构成的集合\(\mathcal H_2\)和10次函数构成的集合\(\mathcal H_{10}\)来拟合这些训练数据,最终得到的\(g_2,g_{10}\)如上图,可见,在左右两种情况下,\(g_2\)的训练误差都比\(g_{10}\)大,但\(g_2\)泛化误差更小
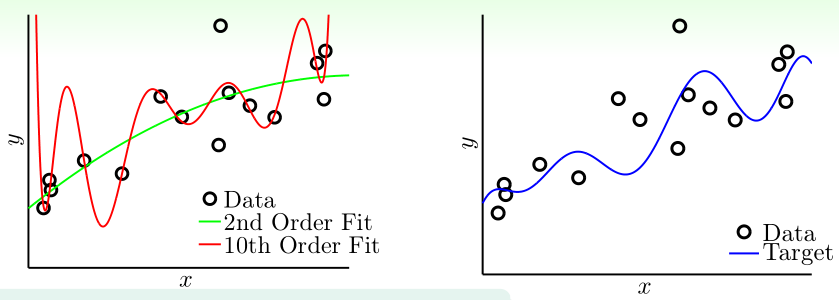
首先看左图的情况(目标函数为10阶,训练样本有噪声)。在Lecture 12中我们知道:
- 对于同样的训练数据,\(\mathcal H_{10}\)的\(E_{in}(g)\)小于等于\(\mathcal H_{2}\)的\(E_{in}(g)\)(g是学习算法从H中选出的训练误差最小的假设函数)
- \(\mathcal H_{10}\)的\(d_{VC}\)大于等于\(\mathcal H_{2}\)的\(d_{VC}\),表明\(\mathcal H_{10}\)的\(E_{in},E_{out}\)之间的gap要远大于\(\mathcal H_{2}\)的gap
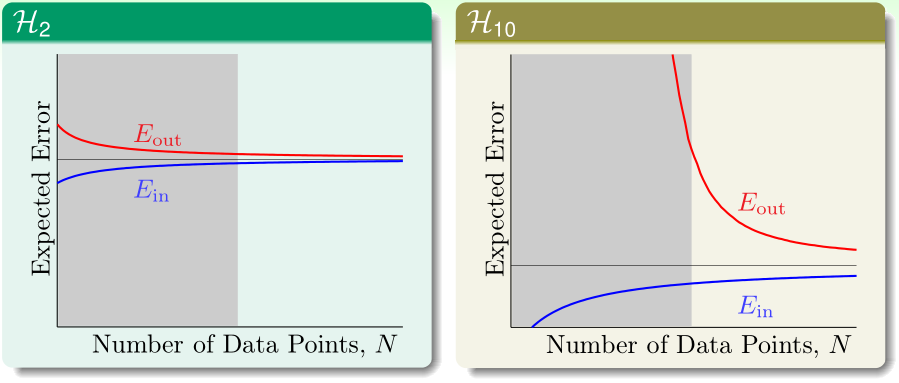
据此我们可以画出\(\mathcal H_{2}\)和\(\mathcal H_{10}\)的学习曲线,训练样本数n在灰色区域时,\(\mathcal H_{10}\)的\(E_{in}\)足够小,但与\(E_{out}\)之间的gap太大,由于n太有限,\(\mathcal H_{10}\)选出了能很好拟合有噪声的训练样本的\(g_{10}\),但\(g_{10}\)不能推广到没有噪声的理想目标函数\(f(x)\)的情况,此时就发生了过拟合。
在这里,训练样本的噪声被称为随机噪声(stochastic noise)
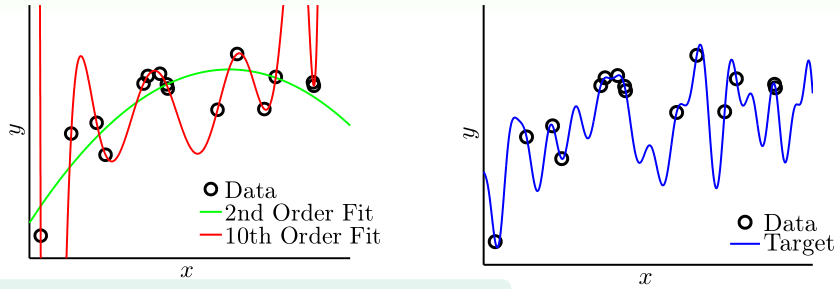
再来看右图的情况(目标函数为50阶,训练样本无噪声),此时依然是\(\mathcal H_2\)中选出的\(g_2\)表现更好
在这个情况里,由于训练样本太少时\(\mathcal H_{10}\)也会发生过拟合,因此我们也可以认为它是有"噪声"的,把它当作是有确定噪声(deterministic noise)的情况:目标函数过于复杂,而已知的训练样本又太少
Deterministic Noise
在前一节的问题中,对于每个训练样本的真实输出值y,我们可以看作是输入x给理想的目标函数f(x)(阶数为\(Q_f\)),然后加上高斯噪声\(\epsilon\)(\(\epsilon\sim \mathcal N(0,\sigma^2)\))的结果,则\(y\sim \mathcal N(f(x),\sigma^2)\)
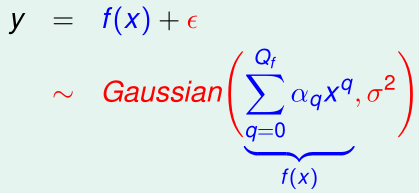
其中,阶数\(Q_f\)可以表示目标函数的复杂度,\(\sigma^2\)可以表示噪声的大小
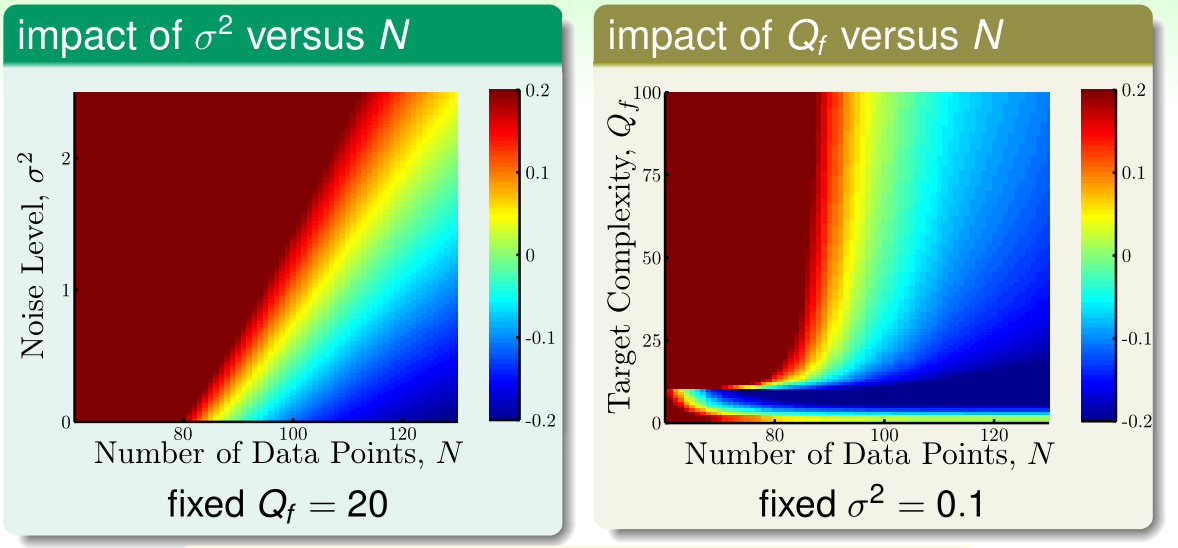
我们用\(E_{out}(g)-E_{in}(g)\)表示过拟合的程度,上图左侧是\(E_{out}(g)-E_{in}(g)\)关于\(\sigma^2,n\)的图像(\(Q_f\)固定为20),右侧是\(E_{out}(g)-E_{in}(g)\)关于\(Q_f,n\)的图像(\(\sigma^2\)固定为0.1)
可见在过拟合中,\(Q_f\)起到了类似随机噪声\(\sigma^2\)的效果,n不变时,\(Q_f\)越大,过拟合程度越大,所以我们称之为deterministic noise
由上图可见,引发过拟合的因素有:
- 1、训练样本数\(n\)太小
- 2、随机噪声\(\sigma^2\)太大
- 3、目标函数复杂度\(Q_f\)太大
- 4、假设函数复杂度(VC维)太大(上图右侧\(Q_f,n\)都很小时,\(Q_f\)<假设函数复杂度的情况)

