机器学习基石(林轩田)学习笔记:Lecture 10 & Lecture 11

Lecture 10:Logistic Regression

Logistic Regression Problem

在之前使用PLA/口袋算法实现线性二分类时，我们理想的目标函数\(f(x)\)的输出\(\in\{1,-1\}\)

而逻辑回归理想的目标函数\(f(x)=P(y=1|x)\)(给定x时其标签y=1的概率)，\(f(x)\in\{1,-1\}\)

在逻辑回归中，理想中没有噪声的训练样本的\(y^{(i)}\)应该是\(P(y=1|x^{(i)})\)，但实际上给出的有噪声的训练样本的\(y^{(i)}\)则是服从概率分布\(P(y|x^{(i)})\)的随机变量的观测值

设输入特征为\(x=(x_0,\cdots,x_d)^T,x_0=1\),逻辑回归的假设函数为\(h(x)=\theta(w^Tx),\theta(x)\)是sigmoid函数

Logistic Regression Error

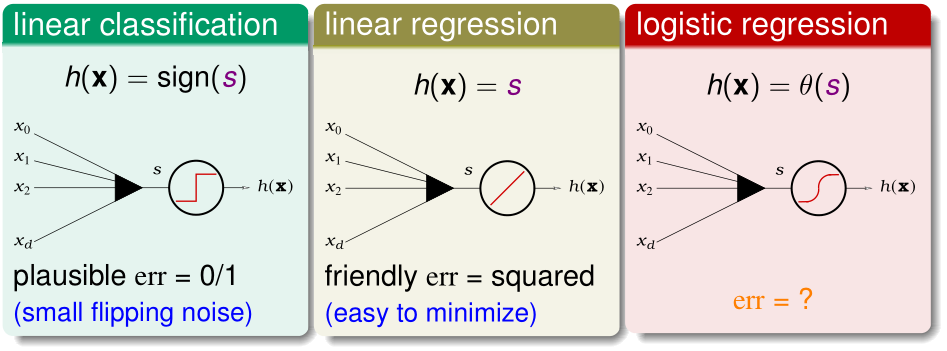
PLA/口袋算法、线性回归、逻辑回归的假设函数都可以视为输入特征的加权之和\(w^Tx\)，经激励函数h(x)处理后得到的结果。

• PLA/口袋算法的h(x)就是sign(x)，误差函数err为0/1误差;
• 线性回归的h(x)就是y=x，误差函数err为平方误差;
• 逻辑回归的h(x)就是sigmoid(x)，下面用极大似然估计的方法得到它的误差函数

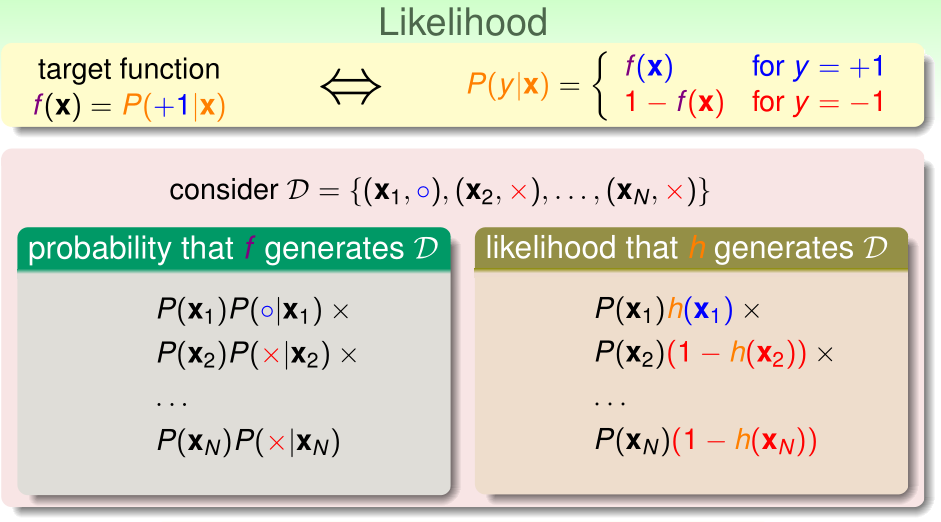
首先介绍似然性(likelihood)。对于目标函数\(f(x)=P(y=1|x)\)，给出\(x^{(1)},\cdots,x^{(n)}\)，通过这个目标函数随机得到\(y^{(1)},\cdots,y^{(n)}\)的概率为

\[\prod_{i=1}^n P(x^{(i)})P(y=y^{(i)}|x^{(i)}) \]

似然性直白地讲，就是用我们的假设函数h(x)代替理想的目标函数f(x)，产生\(y^{(1)},\cdots,y^{(n)}\)的概率

学习算法找到的假设函数h越接近理想的f(x)，似然性就越大。所以学习算法的优化目标就是最大化似然函数

逻辑回归的假设函数\(h(x)=\theta(w^Tx)\),\(1-h(x)=h(-x)\)，这个式子之后会大大方便简化表达式

对于假设函数h而言，其似然函数：

\[\mathcal L(h)=\prod _{i=1}^n P(x^{(i)})h(y^{(i)}x^{(i)}) \]

\[\arg \max_{h} \prod _{i=1}^n P(x^{(i)})h(y^{(i)}x^{(i)})=\arg \max_{h}\prod _{i=1}^n h(y^{(i)}x^{(i)}) \]

而\(\arg \max_{h}\prod _{i=1}^n h(y^{(i)}x^{(i)})\)就是要找到\(\arg \max_{w}\prod _{i=1}^n \theta(y^{(i)}w^Tx^{(i)})\)，对该优化目标取对数

\[\arg \max_{w}\prod _{i=1}^n \theta(y^{(i)}w^Tx^{(i)})=\arg \max_{w}\sum _{i=1}^n \ln \theta(y^{(i)}w^Tx^{(i)}) \]

\[=\arg \min_{w}\frac 1 n \sum _{i=1}^n -\ln \theta(y^{(i)}w^Tx^{(i)}) \]

\[=\arg \min_{w}\frac 1 n \sum _{i=1}^n \ln (1+\exp(-y^{(i)}w^Tx^{(i)})) \]

err(w,x,y)=\(\ln (1+\exp(-y^{(i)}w^Tx^{(i)}))\)，这被称为交叉熵误差

Gradient of Logistic Regression Error

根据之前使用极大似然估计的推导，

\[E_{in}(w)=\frac 1 n \sum _{i=1}^n \ln (1+\exp(-y^{(i)}w^Tx^{(i)})) \]

\(E_{in}(w)\)是连续、二阶可微的凸函数，我们令\(\nabla E_{in}(w)=0\)即可得到最优的参数\(w\)

Gradient Descent

直接令\(\nabla E_{in}(w)=0\)是得不到解析解的，我们只能考虑使用迭代的方式最优化这个参数w

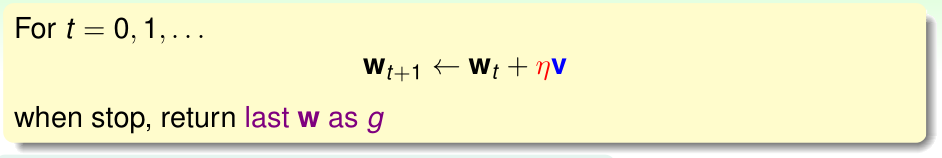
这里的向量v是单位方向向量，\(\eta\)是学习率(步长)，我们知道，沿着与梯度相反的方向走，下降速度是最快的。所以这里v取与梯度相反方向的方向向量：

将这个v代入上式：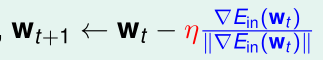

此时每次下降的步长都是相同的(步长为\(\eta\))，而我们希望随着"坡度"越缓，步长越小，令\(\eta'=\frac \eta {\|\nabla E_{in}(w_t)\|}\)，则：

\[w_{t+1}\gets w_t -\eta '\nabla E_{in}(w_t) \]

\(\eta'\)不变，则"坡度"越缓，\(\|\nabla E_{in}(w_t)\|\)越小，步长也就越小

Lecture 11:Linear Models for Classification

Linear Models for Binary Classification

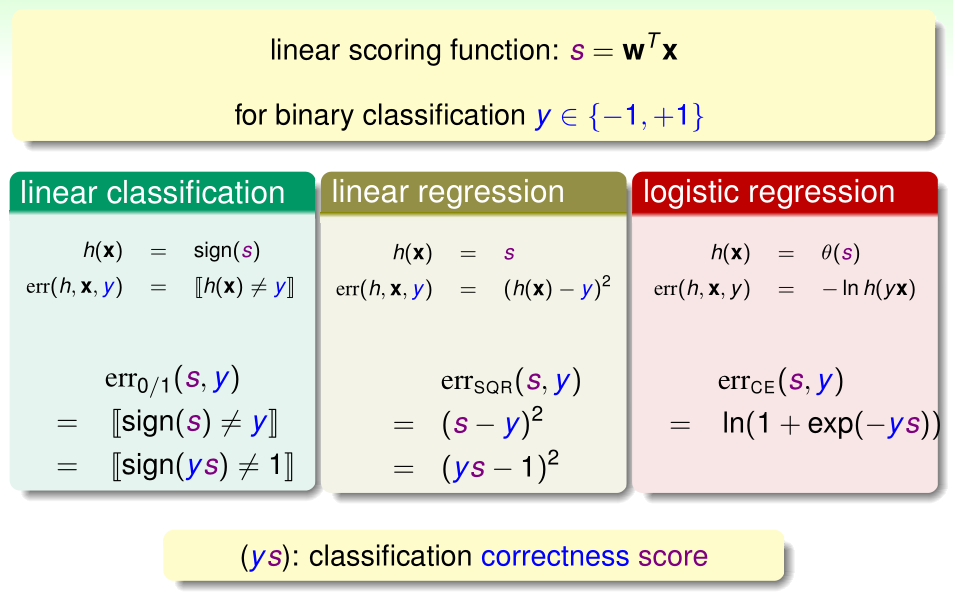
首先我们回顾之前学过的三种二分类算法(线性分类(PLA/口袋算法实现),线性回归实现二分类,逻辑回归)的假设函数与误差函数

为了统一起见，我们令\(s=w^Tx\)，把标签y与s尽量放到一起，\(ys\)可以表示分类的正确程度：

• 在线性分类(PLA/口袋算法)，\(ys>0\)说明分类正确(误差值为0)，\(ys<0\)表示分类错误(误差值为1)
• 在线性回归实现二分类中，\(ys\)越接近1，表明正确度越高(误差值越小)
• 在逻辑回归中，\(ys>0\)说明分类正确，\(ys<0\)表示分类错误；而且\(ys>0\)时其值越大，表明输出正确标签的置信度越大(误差值越小)，在\(ys<0\)时其值越小，表明错得越离谱(误差值越大)

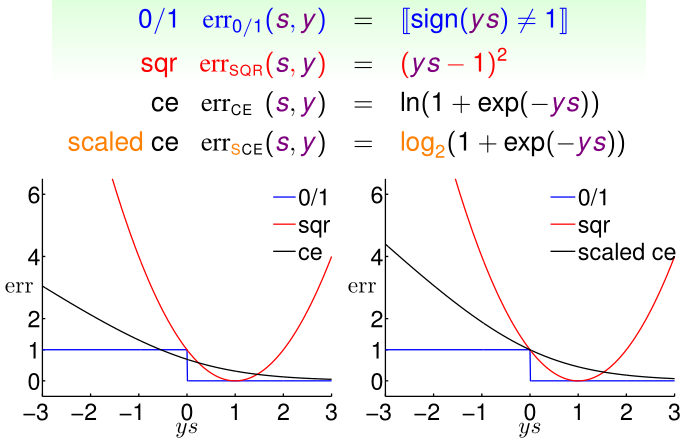
我们把三类算法的误差函数(0/1误差、平方误差、交叉熵误差)关于ys的图像画在直角坐标系中，可见\(err_{CE}\)并不是永远大于等于\(err_{0/1}\)，所以我们做个小trick：用\(\log_2\)代替交叉熵误差中的\(\ln\)，得到\(err_{SCE}\)(scaled cross-entropy)，这样就可以保证\(err_{SCE}\geq err_{0/1}\)了，\(err_{SCE}=\frac 1 {\ln 2}err_{CE}\)

此时，\(\forall y,s(s=w^Tx)\)，我们有：

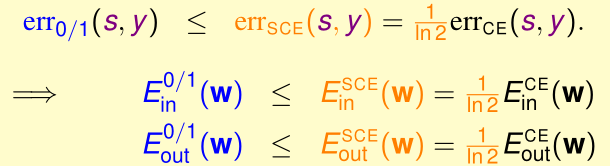
在PLA/口袋算法中，有VC Bound：

\[E_{out}^{0/1}(w)\leq E_{in}^{0/1}(w)+\Omega^{0/1} \]

将代进去，得到：

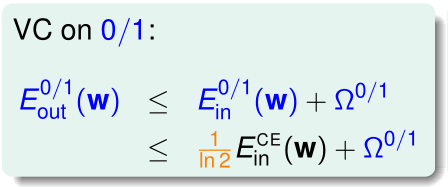
在逻辑回归中，我们也有类似的VC Bound:

\[E_{out}^{CE}(w)\leq E_{in}^{CE}(w)+\Omega^{CE} \]

代入到，得到：

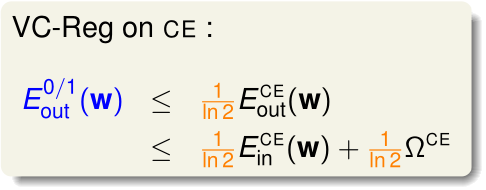
所以，在逻辑回归中，我们只要保证最后得到\(E_{in}^{CE}(g)\approx 0,E_{in}^{CE}(g)\approx E_{out}^{CE}(g)\)，就能给\(E_{in}^{0/1}(g),E_{out}^{0/1}(g)\)确定上限，保证这两个也接近于0，所以说逻辑回归实现二分类是可行的

Stochastic Gradient Descent

CS229和ng在coursera上的课都讲了随机梯度下降，这里不再赘述

Multiclass via Logistic Regression

One vs. All

OVA的方法在CS229和ng在coursera上的课都讲过，这里不再赘述

OVA最大的问题是样本不平衡，即每次分类的正样本数目一般明显小于负样本数目，这会影响最后的分类效果

One vs. One

对于K分类问题，OVO的方法是做\(\frac {K(K-1)} 2\)次分类，每次对训练集中标签为第i类和第j类的训练样本(\(i\neq j\))进行分类，这样就得到了\(\frac {K(K-1)} 2\)个分类器

在对未知的新样本分类时，我们用\(\frac {K(K-1)} 2\)个分类器对这个样本做分类，每个分类器输出它的预测标签，我们用这\(\frac {K(K-1)} 2\)个预测标签做投票，选其中出现次数最大的那个标签作为最终分类结果

OVO的优点是：高效(虽然看上去要训练\(\frac {K(K-1)} 2\)个分类器，但每个分类器只用了训练集中很少的训练样本)，而且解决了OVA正负样本不平衡的问题

OVO的缺点是：对\(\frac {K(K-1)} 2\)个分类器，每个分类器要单独存一个参数\(w_{i,j}\)，所需存储空间更多，而且在预测时，要把输入特征同时给\(\frac {K(K-1)} 2\)个分类器做分类，预测分类的速度比OVA更慢

答案：(2)
理由：10分类问题，OVO方法要训练10x9/2=45个分类器，每个分类器的训练样本数为2n/10，那么总共训练费时为\(45\times (\frac {2n}{10})^3=\frac 9 {25} n^3\)
在这个问题中，使用OVA方法则要训练10个分类器，每个分类器训练样本数为n，总共训练费时为\(10n^3\)，可见在这里，OVO比OVA的训练时间短很多