机器学习基石(林轩田)学习笔记:Lecture 8 & Lecture 9
Lecture 8:Noise and Error
Noise and Probabilistic Target
一般来说,训练集上是有噪声(noise)的,例如:
- 1、少量训练样本的标签是错的(被人类专家错误分类)
- 2、多个训练样本有着同样的输入特征,但分类标签不同
- 3、训练样本的输入特征不准确
回顾之前的弹珠罐子问题。每个弹珠(\(x^{(i)}\sim P(x),y^{(i)}=f(x^{(i)})\))的颜色是绿色还是橙色(\(1\{f(x)\neq h(x)\}\)),这是确定无疑的。
现在,假设每个训练样本的真实标签\(y^{(i)}\sim P'(y|x)\),那么每个弹珠的颜色(\(1\{y\neq h(x)\}\))是不确定的
可以证明,VC理论在\(x^{(i)}\)是独立同分布(服从概率分布P(x)),\(y^{(i)}\)是独立同分布(服从概率分布P(y|x))时依然成立。
我们可以将\(P(y|x)\)视为由理想的目标函数(mini-target)\(f(x^{(i)})\)在点x的取值+噪声决定的,\(f(x^{(i)})=\arg \max_{l}P(y=l|x^{(i)})\),例如\(P(y=1|x^{(i)})=0.7\),\(P(y=-1|x^{(i)})=0.3\),那么在单个\(x^{(i)}\)上理想的\(f(x^{(i)})=1\)
学习算法的任务是,在给定训练集(输入特征x服从分布P(x))时,预测理想的mini-target \(f(x)\)
当没有噪声时,我们可以视为是
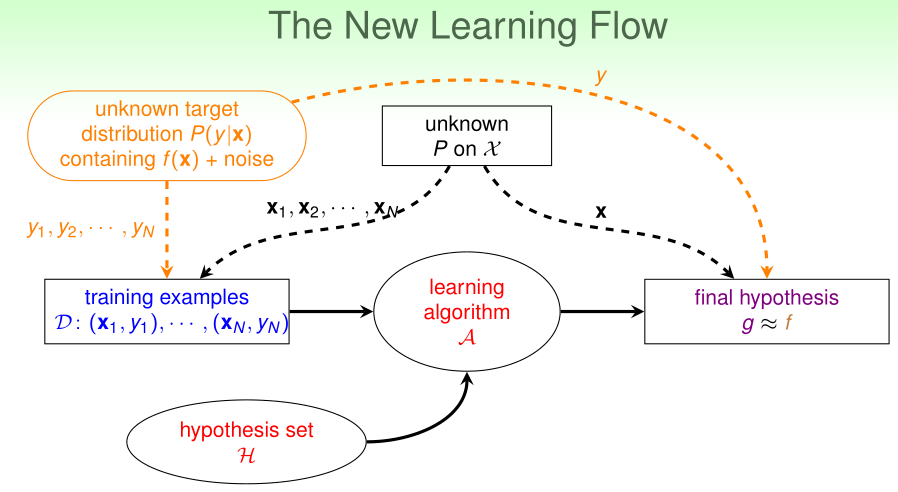
在有噪声的情况下,整个学习过程如上图所示,我们不知道数据输入特征\(x\)的概率分布\(P(x)\),也不知道在给定输入特征x的条件下,标签\(y\)的分布\(P(y|x)\),我们只知道n个训练样本(观测数据)\((x_1,y_1),\cdots,(x_n,y_n)\)

答案:(4)
理由:
- (1)错误,因为已知训练集D是线性可分时,我们也差不多找到了可以完美分类所有样本的参数\(w^*\)
- (2)错误,因为D不是线性可分,可能是由于D中有噪声导致的,采用口袋算法即可。
- (3)错误,因为有可能碰巧D是线性可分的,而真正的所有数据的分布情况是线性不可分的。
Error Measure
我们用误差函数\(E(g,f)\)来表示学习算法最终选取的假设函数g与理想的目标函数f之间的差异
泛化误差(out-of-sample error)是在所有(未知的)输入特征\(x\)下的分类误差的平均值。也可以说是在输入特征\(x\sim P(x)\)下分类误差值的期望。
我们定义单点误差(pointwise error)为在单个训练样本上的误差值:err(g(x),f(x))
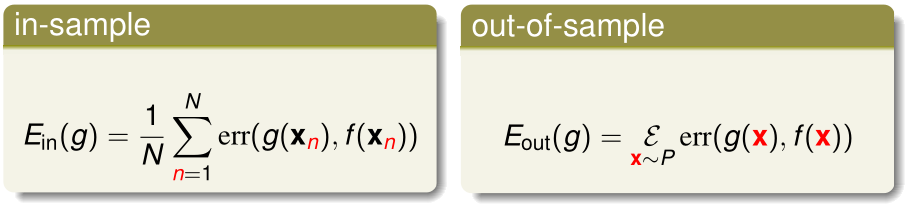
经验误差可以看作是n个训练样本的单点误差的平均值,泛化误差可以看作是输入特征x服从分布P(x)时,单点误差的期望

单点误差分为0/1误差(也叫分类误差,一般用于分类问题)和平方误差(一般用于回归问题)

如果标签\(y\in\{1,2,3\}\),已知给定x的情况下\(P(y|x)\),从上图可见,不同的误差函数(0/1误差和平方误差)对理想目标函数在该点x的取值f(x)的影响
对于大多数假设函数集合\(\mathcal H\)和单点误差函数err而言,VC理论都是适用的。
Algorithmic Error Measure

如上图,对于二分类问题而言,我们可以对错误的分类作如下两种归类:
- 真实输出为1,假设函数输出为-1的为false reject(对应ng的课里的false negative)
- 真实输出为-1,假设函数输出为1的为false accept(对应ng的课里的false positive)

在超市的指纹识别中,假设函数输出分类为1表示给优惠,-1表示不给优惠;如果有本来不该优惠的顾客得到了优惠不要紧,但该优惠的顾客没得到优惠后果很严重,所以此时我们希望尽量少出现false reject,所以让false reject的惩罚系数取更大的值

在CIA的指纹系统中,如果有员工刷了指纹没通过不要紧,但如果有不法分子刷了指纹通过了,后果很严重,所以此时我们希望少出现false accept,它的惩罚系数取更大的值。
Weighted Classification

在CIA指纹系统的问题中,为了减少false accept,我们需要采用加权的泛化误差和经验误差,定义如上图所示。
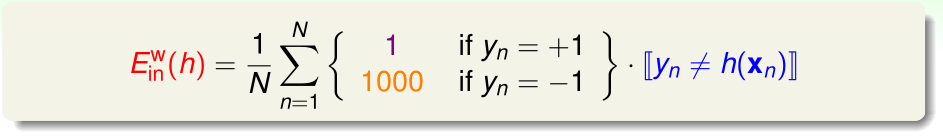
进一步地,我们可以令这个新的(加权)经验误差为\(E_{in}^W(h)\),其定义如上图,在口袋算法中,我们用这个\(E_{in}^W(h)\)替代当时用的不加权的\(E_{in}(h)\)即可。

实际上,在这个问题中,我们只需要把训练样本中标签\(y^{(i)}=-1\)的样本复制1000遍,套用之前已有的口袋算法便能达到一样的效果。因为这样做,使用之前的口袋算法,每次抽样碰到标签为-1的概率变大了1000倍。
Lecture 9:Linear Regression
Linear Regression Problem
给出输入特征\(x=(x_0,x_1,\cdots,x_d),x_0=1\),预测对应的输出值\(y\approx \sum_{i=0}^dw_ix_i\),线性回归的假设函数可以表示为\(h(x)=w^Tx\)(这个假设函数很像感知机的假设函数,只是去掉了sign())
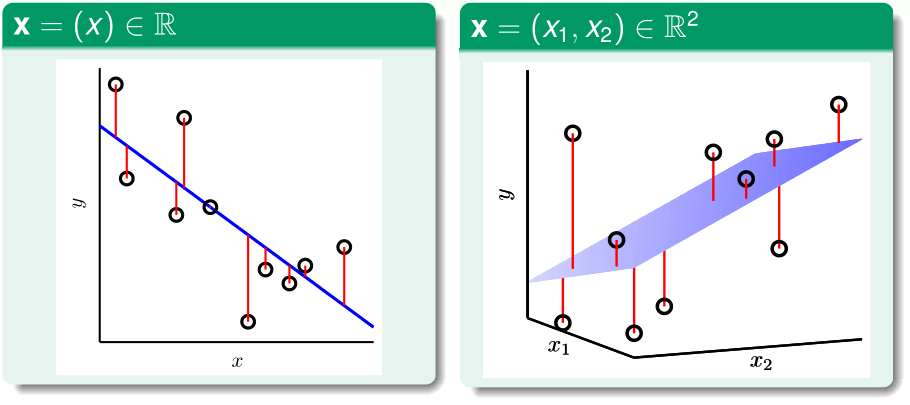
上图中,蓝色的就是假设函数(d=1是直线,d=2是平面),红色的线段表示的就是真实输出值和预测值之间的差异
在线性回归问题中,误差函数err采用平方误差:\(err(\hat y,y)=(\hat y-y)^2\),相应地,经验误差和泛化误差分别为:

Linear Regression Algorithm
\(E_{in}(w)\)用矩阵的形式表示如下:
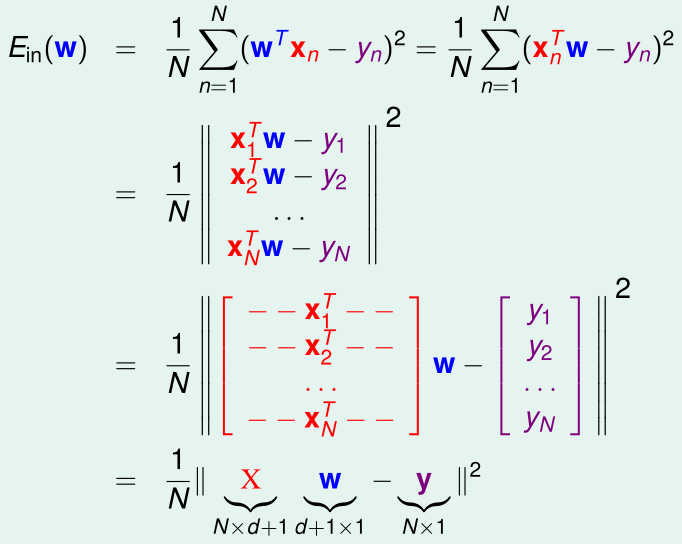
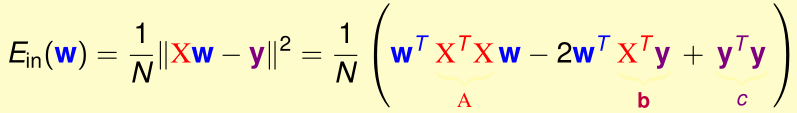
(这里用到了\(|x|^2=x^Tx\))
\(E_{in}(w)\)是连续可微的凸函数。令\(\nabla E_{in}(w)=0\),就能得到\(E_{in}(w)\)最小的w:
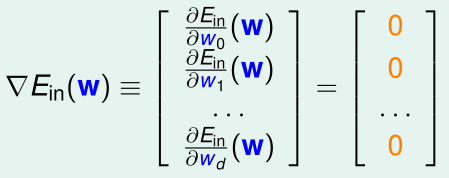
一般在\(n\gg d+1\)时,\(X^TX\)可逆,此时可以直接得到w
当\(X^TX\)为奇异阵时,\(w=(X^TX)^{-1}X^Ty=X^+y\),\(X^+\)是\(X\)的伪逆,我们通过其他方式可以得到\(X^+\),从而求出w

答案:(3)
理由:\(\hat y=Xw_{LIN}=XX^+y\)
Generalization Issue
因为我们求得的\(w_{LIN}\)是解析解,所以可以用比VC理论更简单的方式证明\(E_{in}\approx E_{out}\)
根据之前的线性回归的经验误差的定义,我们有:
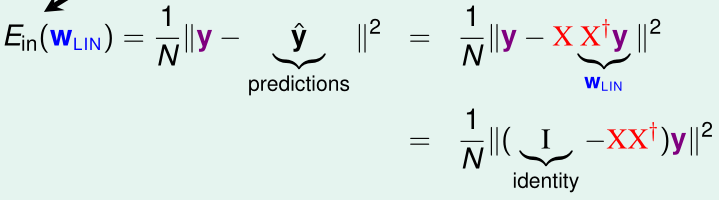
(我们称\(XX^+\)为hat matrix \(H\),也就是X的列空间的投影矩阵)
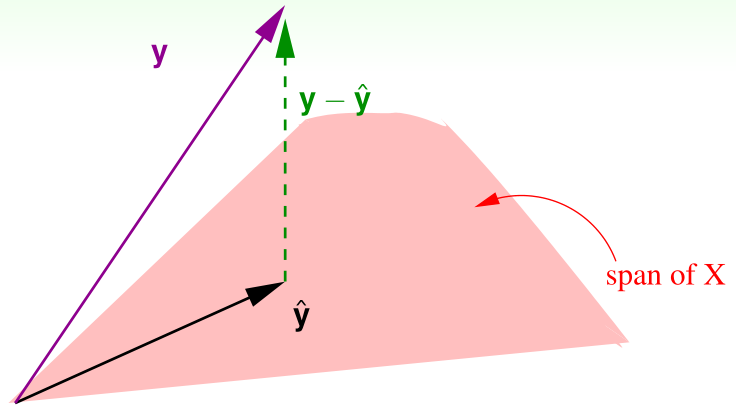
我们对n个输入特征的n个预测值构成的列向量\(\hat y=Xw_{LIN}\in C(X)\),如上图所示,可以直观看出\(\hat y\)在X的列空间中,我们要最小化的\(E_{in}(w_{LIN})\)则是向量\(y-\hat y\)的模长,显然\(y-\hat y\)垂直于X的列空间时\(y-\hat y\)的模长最小
而\(H\)是X的列空间的投影矩阵,向量y通过投影矩阵H投影到X的列空间中得到\(\hat y=Hy\),那么通过\((I-H)y\)则可以得到\(y-\hat y\perp C(X)\)
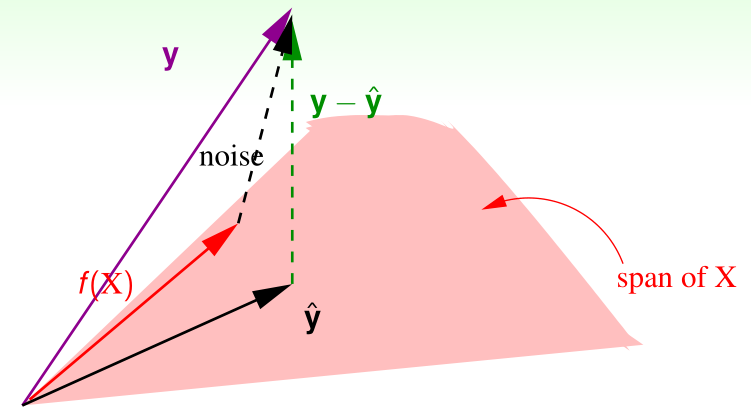
上图中,f(X)是最理想的目标函数,而真实输出值\(y=f(X)+\)噪声noise,可以发现,\(noise\)投影到X的列空间后得到的\(H\ noise=\hat{noise}\)和\(noise\)之间的差异也是\(y-\hat y\),
于是,
用向量noise范数的平方\(\|noise\|^2\)表示noise level,就能得到\(E_{in}\)的规模了,课程也给出了\(E_{out}\)的规模,但证明复杂,这里略去
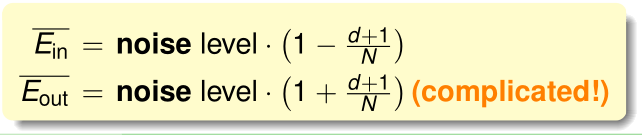
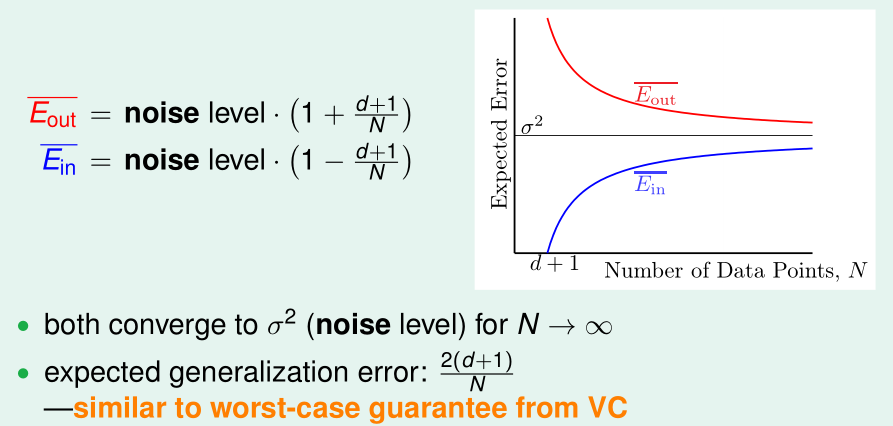
随着训练样本数n增大,\(\bar E_{in},\bar E_{out}\)将收敛于noise level
Linear Regression for Binary Classification

之前介绍的线性分类算法(PLA、口袋算法),输出值要么为1,要么为-1,误差函数用0/1误差;而这里的线性回归输出值在整个实数域内,误差函数为平方误差,可以快速得到解析解。
实际上线性回归算法也可以用于分类,我们直接把每个样本的标签当作线性回归问题的真实输出值即可。
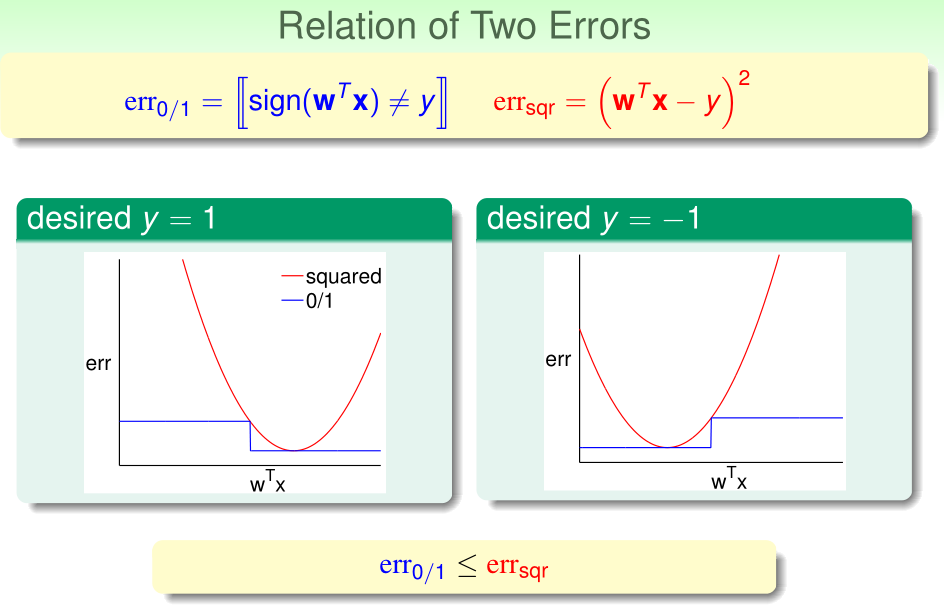
在分类问题中,可以证明,对于任意的\(w^Tx\),这里的线性回归的平方误差总是大于之前PLA/口袋算法的0/1误差
在PLA/口袋算法中,根据VC Bound,有:
又\(E_{in_{classification}}\leq E_{in_{regression}}(w)\),从而:
所以这里用线性回归问题解决二分类的Eout也是有上界的,虽然这个上界比PLA/口袋算法的Eout上界高,但是实际上线性回归解决二分类也是可行的,而且它也可以为PLA/口袋算法初始化参数w,从而加速学习过程。

