机器学习基石(林轩田)学习笔记:Lecture 6 & Lecture 7

Lecture 6:Theory of Generalization

对于n个点\(x^{(1)},\cdots,x^{(n)}\)，break point=k，我们称此时\(\mathcal H\)的成长函数\(m_\mathcal H(n)=B(n,k)\)，可以证明\(B(n,k)\leq n^k\)(而且这个上界很宽松)

根据Lecture 4推得的公式

\[P(\mathcal D\ is\ bad\ for\ all\ h)\leq 2m\exp(-2\epsilon^2n) \]

即

\[P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\leq 2m\exp(-2\epsilon^2n) \]

此时我们希望把其中的m替换为\(n^k\)，但这个替换并不是简单的替换，其中证明很复杂，这里省去，最终可以得到

\[P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\leq 2\cdot 2m_\mathcal H(2n)\exp(-2\frac 1 {16}\epsilon^2n) \]

\[P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\leq 4m_\mathcal H(2n)\exp(-\frac 1 8\epsilon^2n) \]

我们称这个引入成长函数的新不等式为VC(Vapnik­-Chervonenkis) bound

而在已知break point=k时，\(m_\mathcal H(n)=O(n^k)\)，此时我们可以说机器是可以学习的，能够保证\(E_{in}(g)\approx E_{out}(g)\)。

Lecture 7:The VC Dimension

Definition of VC Dimension

之前我们已经定义了假设函数集\(\mathcal H\)的break point，break point是满足\(m_\mathcal H(n) <2^n\)的最小的n

而假设函数集\(\mathcal H\)的VC维\(d_{VC}(\mathcal H)\)是存在一组\(x^{(1)},\cdots,x^{(n)}\)，满足\(m_\mathcal H(n) =2^n\)的最大的n

或者说，存在n个点\(x^{(1)},\cdots,x^{(n)}\)，不论这n个点标签是怎样的，都能从\(\mathcal H\)中找到一个h对它们全部正确分类(即存在\(h\in \mathcal H\)能shatter这n个点)

根据上述定义，显然有\(d_{VC}(\mathcal H)=\)break point(\(\mathcal H\))-1

回顾Lecture 5中\(\mathcal H\)分别为positive rays、positive intervals、convex sets以及2D感知机时的\(m_\mathcal H(n)\)，我们可以得到对应的\(d_{VC}\)

当\(n\geq 2,d_{VC}\geq 2\)时，我们有\(m_\mathcal H(n)\leq n^{d_{VC}}\)，在我们已知\(d_{VC}\)时，Lecture 6的不等式

\[P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\leq 4m_\mathcal H(2n)\exp(-\frac 1 8\epsilon^2n) \]

中的\(m_\mathcal H(2n)\)就可以被替换掉：

\[P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\leq 4m_\mathcal H(2n)\exp(-\frac 1 8\epsilon^2n) \]

\[\leq 4(2n)^{d_{VC}}\exp(-\frac 1 8\epsilon^2n) \]

则\(P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\)的上界就只与n有关了。

答案：(4)
理由：题目条件只告诉我们，存在一组n个点不能被\(\mathcal H\) shattered，但我们不能判定是否存在一组n个点可以被\(\mathcal H\) shattered，也就无法推断\(d_{VC}(\mathcal H)\)了

VC Dimension of Perceptron

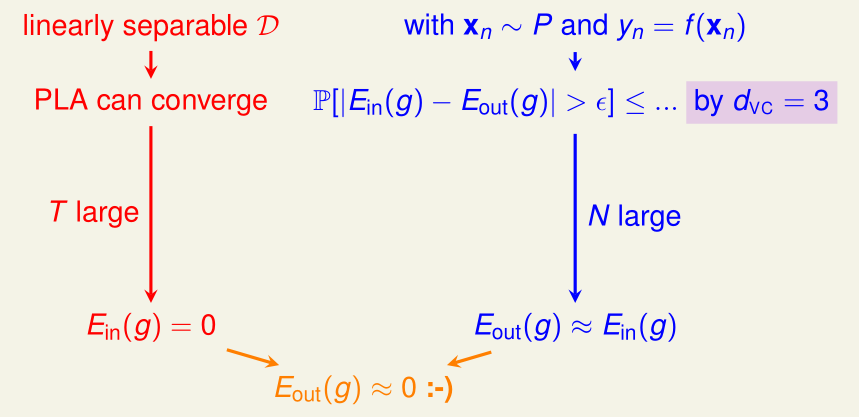
对于2D感知机而言，假设训练集\(\mathcal D\)线性可分，那么经过足够多次迭代，我们能找到一个假设函数\(g,E_{in}(g)=0\)

而所有的输入数据\(x{(n)}\sim P,y^{(n)}=f(x^{(n)})\)(f(x)是我们未知的一个函数)

由于2D感知机的\(d_{VC}=3\)，所以\(P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\)有一个确定的、只关于n的上界，n足够大时，\(E_{out}(g)\approx E_{in}(g)\)

下面我们把2D感知机的VC维，推广到d-D感知机的情况(d>2)：\(d_{VC}=d+1\)

首先证明,d-D感知机\(d_{VC}\geq d+1\):

我们可以构造一组d+1个点，使得它们能被d-D感知机的\(\mathcal H\) shattered:

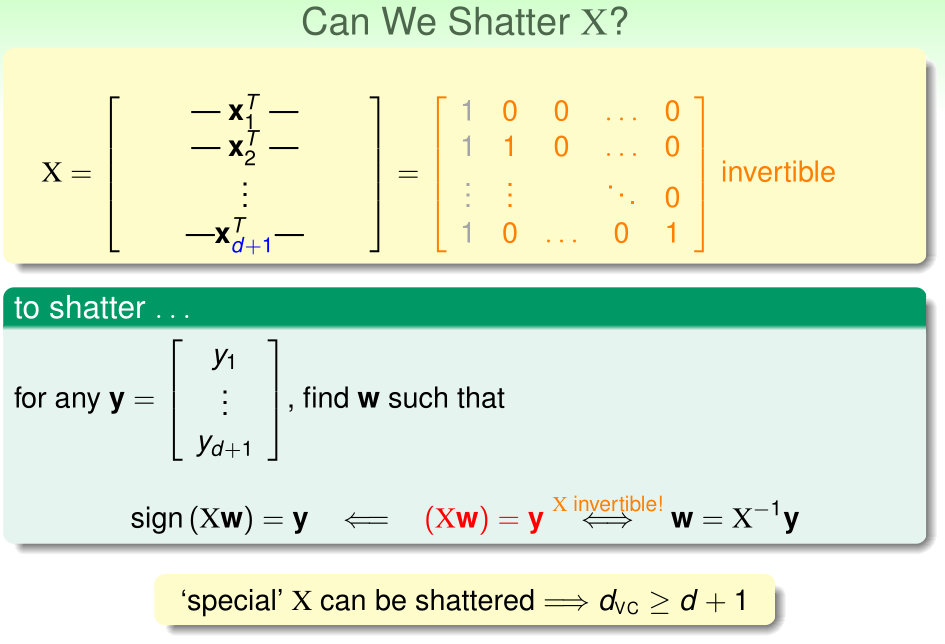
(注意第一列灰色的1对应于偏置)

显然这样的d+1个输入数据构成的矩阵\(X\)可逆，对于任意的标签列向量\(y\)，令\(Xw=y,w=X^{-1}y\)，此时显然有\(\mathrm{sign}(Xw)=\mathrm{sign}(y)=y\)，所以这d+1个点能被shattered

再证明，d-D感知机\(d_{VC}\leq d+1\):

此时d+2个输入数据构成的矩阵\(X\)，\(r(X)\leq d+1\)，所以行向量组线性相关，不妨设\(x_{d+2}\)可以被其他d+1个行向量线性表示(如果不能的话，找一个可以被其他行向量线性表示的\(x_i\)交换到\(x_{d+2}\))

\[x_{d+2}=a_1x_1+\cdots a_{d+1}x_{d+1} \]

若\(a_1>0,a_2<0,\cdots,a_{d+1}<0\)，则，如果这d+2个点的标签分别为

\[y_1=\mathrm{sign}(a_1),y_2=\mathrm{sign}(a_2),\cdots,y_{d+1}=\mathrm{sign}(a_{d+1}),y_{d+2}=-1) \]

那么

\[w^Tx_{d+2}=a_1w^Tx_1+a_2w^Tx_2+\cdots+a_{d+1}w^Tx_{d+1} \]

为了满足要求，\(w^Tx_1\)与\(a_1\)同号,......,\(w^Tx_{d+1}\)与\(a_{d+1}\)同号，那么\(a_1w^Tx_1>0,\cdots,a_{d+1}w^Tx_{d+1}>0\)，从而

\[w^Tx_{d+2}=a_1w^Tx_1+a_2w^Tx_2+\cdots+a_{d+1}w^Tx_{d+1}>0 \]

这就导致第d+2个数据分类一定是错误的。

所以对于任意的d+2个点，d-D感知机的\(\mathcal H\)都不能shatter它们。\(d_{VC}(\mathcal H)\leq d+1\)

Physical Intuition of VC Dimension

假设函数集\(\mathcal H\)的VC维决定了假设函数的分类能力(这体现在参数数量上，参数越多)。VC维越大，\(\mathcal H\)的分类能力越强，\(\mathcal H\)能够shatter更多的点。

一般地，VC维\(\approx\)假设函数参数个数(但这个规律在某些时候不成立)

回顾之前所学的内容，机器要想学习，必须满足：

• 1、\(E_{in}(g)\approx E_{out}(g)\)，泛化误差是可以通过假设函数在训练集上的经验误差近似估计的。
• 2、\(E_{in}(g)\)能够做到足够小。这样学习算法才能从\(\mathcal H\)中选取出一个经验误差足够小的g,从而根据(1)保证它的泛化误差足够小，这样学习算法才是有效的。

当\(\mathcal H\)为有限集时：

• (a)\(m=|\mathcal H|\)小，此时根据之前推出的不等式，可以满足(1)，但是由于可供选择的假设函数h太少，不能满足(2)
• (b)\(m=|\mathcal H|\)很大，可选择的假设函数很多，(2)能满足，但是(1)就无法满足了。

类似地，当\(\mathcal H\)为无限集时：

• (a)VC维很小，此时根据之前推出的不等式，可以满足(1)，但是由于假设函数分类能力太弱，不能满足(2)
• (b)VC维很大，假设函数分类能力很强，(2)能满足，但是(1)就无法满足了。

可见合适大小的VC维是非常重要的。

Interpreting VC Dimension

\[P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\leq 4(2n)^{d_{VC}}\exp(-\frac 1 8\epsilon^2n) \]

令\(\delta=4(2n)^{d_{VC}}\exp(-\frac 1 8\epsilon^2n)\)，则，\(\epsilon =\sqrt{\frac 8 n \ln (\frac{4(2n)^{d_{VC}}}{\delta})}\)

那么我们至少有\(1-\delta\)的把握，使得对于所有的\(h\in \mathcal H\):

\[\ |E_{in}(h)-E_{out}(h)|\leq\epsilon=\sqrt{\frac 8 n \ln (\frac{4(2n)^{d_{VC}}}{\delta})} \]

\[E_{out}(h)\leq E_{in}(h)+\sqrt{\frac 8 n \ln (\frac{4(2n)^{d_{VC}}}{\delta})} \]

令\(\Omega=\sqrt{\frac 8 n \ln (\frac{4(2n)^{d_{VC}}}{\delta})}\ \ \mathrm{w.r.t}\ \ n,\mathcal H,\delta\)，则

\[P(\exists h\in \mathcal H\ \mathrm{s.t.}\ |E_{in}(h)-E_{out}(h)|>\epsilon)\leq 4(2n)^{d_{VC}}\exp(-\frac 1 8\epsilon^2n)<\delta \]

我们令误差容忍度\(\epsilon=0.1\)，\(\delta=0.1\)，如果我们已知\(d_{VC}=3\)，那么样本数取多少才合适呢？

从上表可见，理论上我们至少要\(n\approx 10000d_{VC}\)

然而VC Bound这个上界很宽松，实际上一般来说\(n\approx 10d_{VC}\)就够了