机器学习基石(林轩田)学习笔记:Lecture 4 & Lecture 5

Lecture 4:Feasibility of Learning

问题背景

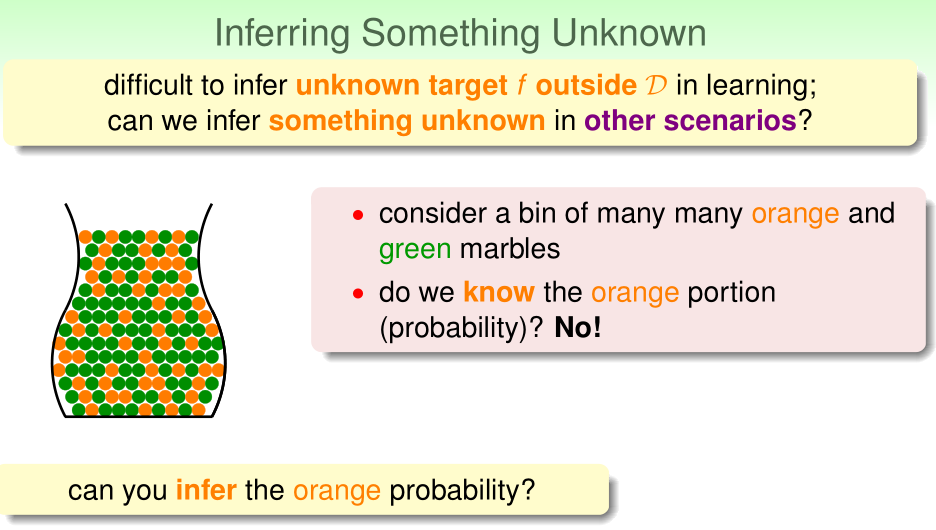
给出一个罐子，其中有若干绿色、橙色弹珠，显然我们无法准确确定其中橙色珠子的比例。

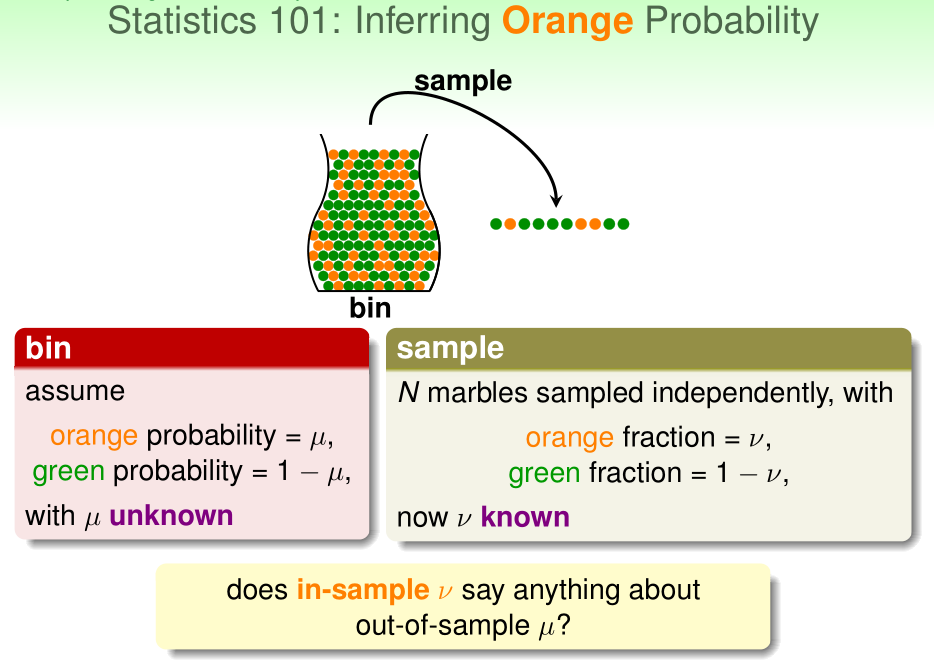
但我们可以通过从其中抽出n个弹珠作为样本来近似估计这一比例。若样本中橙色弹珠比例为\(\nu\),我们估计整个罐子中橙色弹珠比例为\(\mu\)

Hoeffding不等式

Hoeffding不等式可以告诉我们\(\nu\)对\(\mu\)的近似程度。设样本数量为n，则

\[P(|\nu-\mu|>\epsilon)\leq 2\exp(-2\epsilon^2n) \]

我们称"\(\nu=\mu\)"是大致近似正确的(probably approximately correct,PAC)

样本数量n越大、误差容限度\(\epsilon\)越大，\(\nu\approx \mu\)的概率也就越大了。

答案：(3)
理由：\(|\nu-\mu|\geq 0.3,\epsilon=0.3,n=10\)，代入公式计算即可

根据Hoeffding不等式与经验误差来估计假设函数\(h\)的泛化误差

在弹珠罐子问题中，橘色弹珠比例是未知的，采样出来的n个弹珠是独立同分布的(都服从某个伯努利分布)

在机器学习中，对于给定的假设函数\(h(x)\)，我们不知道它是否接近理想中的目标函数\(f(x)\)，我们从无数的数据中采样得到n个已知样本\((x^{(i)},y^{(i)})\)(也就是所谓的训练集\(\mathcal D\))，\(x^{(i)}\)也是独立同分布的(服从概率分布\(P\)),所有的\(x\sim P\)(所有的x服从某个概率分布)，注意训练样本内和样本外的x，都服从概率分布\(\mathcal P\)，这一点非常重要！

现在，我们希望用已知的\(E_{in}(h)=\frac 1 n \sum_{i=1}^n 1\{h(x^{(i)})\neq y^{(i)}\}\)(经验误差)来近似估计\(E_{out}(h)=E_{x\sim P}[1\{h(x^{(i)})\neq y^{(i)}\}]\)(泛化误差)

于是我们可以类比弹珠罐子问题，\(h(x^{(i)})=y^{(i)}\)相当于绿色弹珠，\(h(x^{(i)})\neq y^{(i)}\)相当于橙色弹珠

此时，\(E_{in}(h)\)就相当于样本中橙色弹珠的比例，\(E_{out}(h)\)就相当于罐子中橙色弹珠的比例。

同样根据Hoeffding不等式，我们有

\[P(|E_{in}(h)-E_{out}(h)|>\epsilon)\leq 2\exp (-2\epsilon^2n) \]

于是，只要训练集大小n、误差容忍度\(\epsilon\)足够大，我们就可以说"经验误差=泛化误差"是大约近似正确(PAC)的。此时，学习算法在\(\mathcal H\)中选择经验误差最小的那个假设函数h，就能得到很好的结果(学习算法选择的假设函数\(g\approx\)理想的\(f\))

答案：(2)
理由：之前我们讲的内容，成立的前提条件是，采样得到的样本与全部数据的概率分布是近似的

在\(\mathcal H\)中选取最佳的\(h\)

丢硬币问题

让150个人，每个人丢5次硬币，则有$1-(1-\frac 1 {2^5})>99% $的概率，至少有一个人连续5次丢硬币得到正面朝上，然而这个人手上的硬币和其他人的硬币是一模一样的。

在机器学习问题中，也会遇到类似的情况：在\(\mathcal H\)中选取的经验误差最小的\(h\)(\(E_{in}\)就是一个人丢若干次硬币，正面朝上的比例=0)，有可能泛化误差很大(\(E_{out}\)就是实际上丢硬币正面朝上的概率=1/2)。

坏样本与坏数据

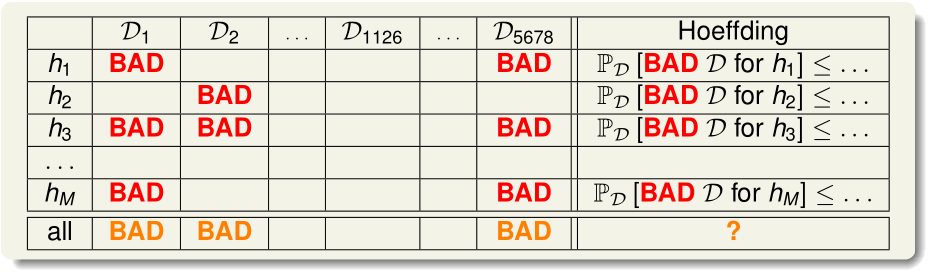
对于给定的假设函数h，我们定义\(E_{in}\)很小而\(E_{out}\)很大(\(|E_{in}(h)-E_{out}(h)|>\epsilon\))的训练集\(\mathcal D\)是坏训练样本(BAD)

\[P(|E_{in}(h)-E_{out}(h)|>\epsilon)=P(\mathcal D\ is\ bad\ for\ h)=\sum_{\mathcal D_i}P(\mathcal D_i)\cdot 1\{\mathcal D_i \ is \ bad\ for\ h\} \]

则训练集\(\mathcal D\)对于全体h而言都是坏的概率

\[P(\mathcal D\ is\ bad\ for\ all\ h)=P(\mathcal D\ is\ bad\ for\ h_1\cup\cdots\cup\mathcal D\ is\ bad\ for\ h_m) \]

\[\leq \sum_{i=1}^m P(\mathcal D\ is\ bad\ for\ h_i) \]

(根据union bound不等式)

\[=\sum_{i=1}^mP(|E_{in}(h_i)-E_{out}(h_i)|>\epsilon) \]

\[\leq 2m\exp(-2\epsilon^2n) \]

这表明在\(\mathcal H\)为有限集时，训练样本n、误差容忍度\(\epsilon\)足够大，就可以说经验误差和泛化误差是PAC的。

Lecture 5:Training versus Testing

Recap

机器学习最终选择的假设函数\(g\)应当满足：

• 1、\(E_{in}(g)\approx E_{out}(g)\)：这保证了泛化误差近似于经验误差
• 2、\(E_{in}(g)\)足够小：这是机器学习算法的训练过程的结果

当\(\mathcal H\)是有限集时，根据Lecture 4得到的公式：

• \(|\mathcal H|\)很小时，能满足第一条，但是由于可供选择的假设函数太少，\(E_{in}(g)\)做不到足够小，无法满足第二条；
• \(|\mathcal H|\)很大时，可选的假设函数足够多，可以选出g使得\(E_{in}(g)\)足够小，但是此时无法满足第一条

然而在感知机算法(以及口袋算法)中，\(|\mathcal H|=+\infty\)，这些算法都能很好地学习，下面谈谈这个问题的原因。

Effective Number of Lines

我们回顾union bound:

\[P(A_1\cup \cdots \cup A_m)\leq P(A_1)+\cdots+P(A_m) \]

不等式取等号，当且仅当\(A_1,\cdots,A_m\)没有交集。然而实际上一般这m个事件是有交集的，上面的上限显然定得太大了。

我们需要把所有假设函数划分成有限个类。划分的依据是：对于给定的n个点\(\{x^{(1)},\cdots,x^{(n)}\}\)，分类\(\{y^{(1)},\cdots,y^{(n)}\}\)完全相同的假设函数划分为同一个类。这样，同一类假设函数的\(E_{in}(h)\)完全相同。

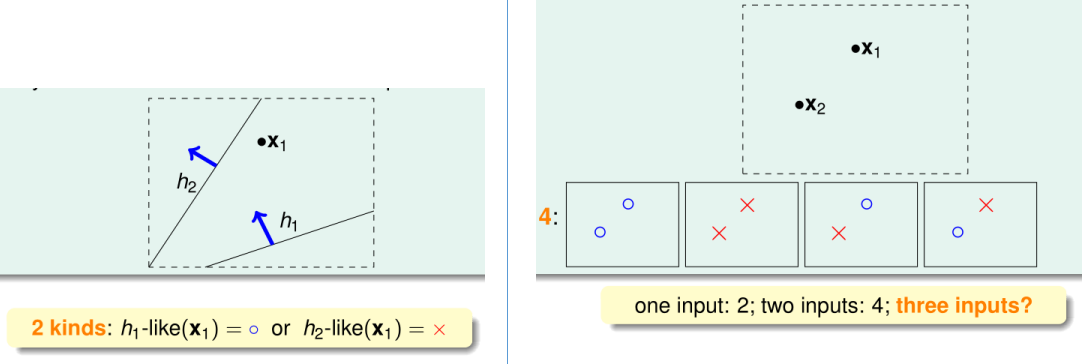
如上图，n=1时有\(2^1=2\)种分类，n=2时有\(2^2=4\)种分类

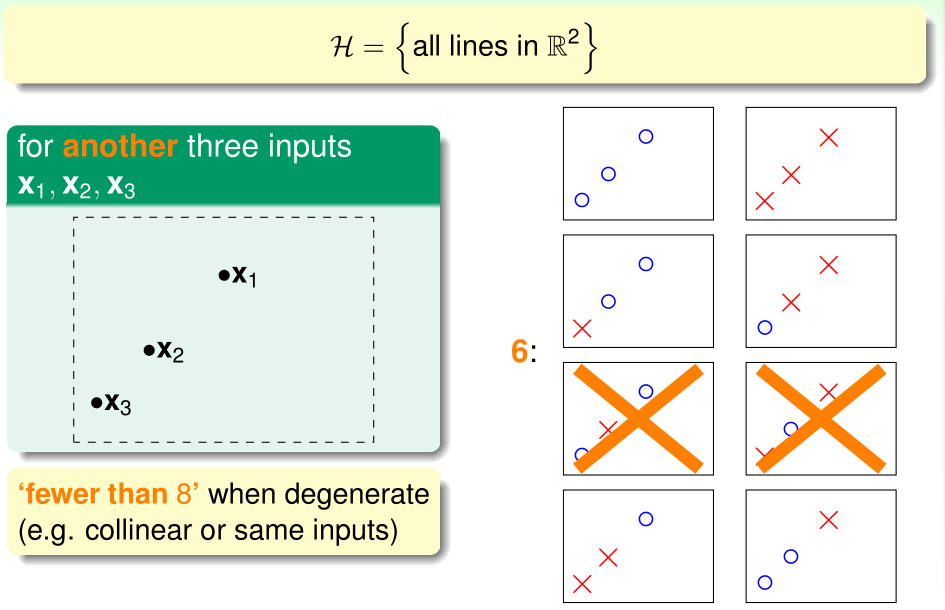
然而，当假设函数集合\(\mathcal H\)为全体决策边界为二维直线的分类器(显然是无限集)时，对于上图给定的三个点，只能把决策函数分为6类，另有2种\(x^{(i)}\)的标签方案是找不到可以完全正确分类的决策函数的。

同样的\(\mathcal H\)在给定上图所示的四个点时，只能将决策函数分为14类，另有2种\(x^{(i)}\)的标签方案是找不到可以完全正确分类的决策函数的。

可见，当假设函数集合\(\mathcal H\)为全体决策边界为二维直线的分类器时，假设函数的类数\(\leq 2^n\)
对于这种无限集\(\mathcal H\)，我们可以把Lecture 4中\(P(\mathcal D\ is\ bad\ for\ all\ h)\leq 2m\exp(-2\epsilon^2n)\)中的m替换成一个数字effective(n)
如果effective(n)\(\ll 2^n\)，那么即使这里的\(|\mathcal H|\)是无限大的，也能做到\(E_{in}(g)\approx E_{out}(g)\),机器学习也是有可能的

Effective Number of Hypotheses

对于假设函数集合\(\mathcal H\)为全体决策边界为二维直线的分类器、给定二维平面上n个点\(x^{(1)},\cdots,x^{(n)}\)时，我们称dichotomy(用符号\(H(x^{(1)},\cdots,x^{(n)})\)表示)是所有假设函数的类别构成的集合。

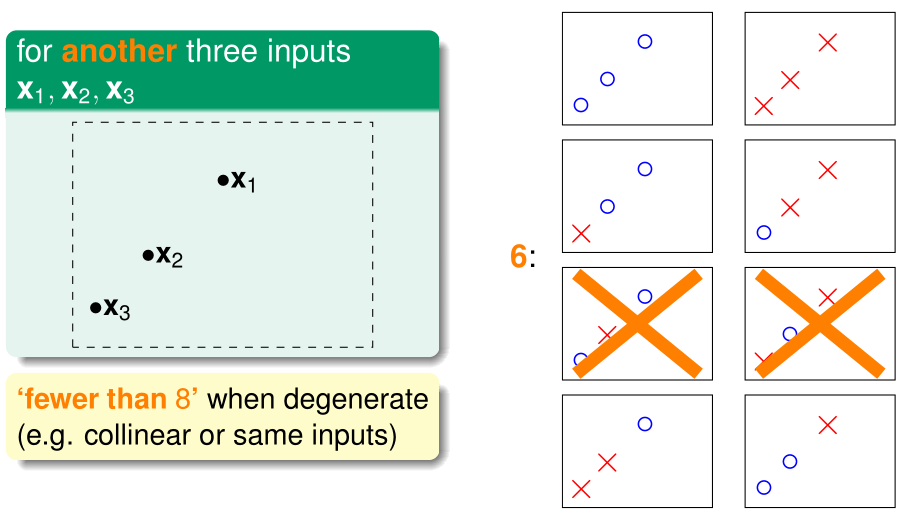
还是用上一节的例子，对于这样给定的三个点\(x^{(1)},x^{(2)},x^{(3)}\)，对应的dichotomy包含6个元素。\(\mathcal H(x^{(1)},x^{(2)},x^{(3)})=6\)

尽管\(|\mathcal H|\)可能是无穷大的，但是根据上一节的证明，我们知道\(|\mathcal H(x^{(1)},\cdots,x^{(n)})|\leq 2^n\)，其大小取决于\(x^{(1)},\cdots,x^{(n)}\)在二维平面中的分布

我们定义成长函数(growth function)\(m_\mathcal H(n)\)为：

\[m_\mathcal H(n)=\max_{x^{(1)},\cdots,x^{(n)}}|\mathcal H(x^{(1)},\cdots,x^{(n)})| \]

显然\(m_\mathcal H(n)\leq 2^n\)

对于由\(h=\mathrm{sign} (x-a)\)构成的集合而言，显然\(m_\mathcal H(n)=n+1\ll 2^n\)

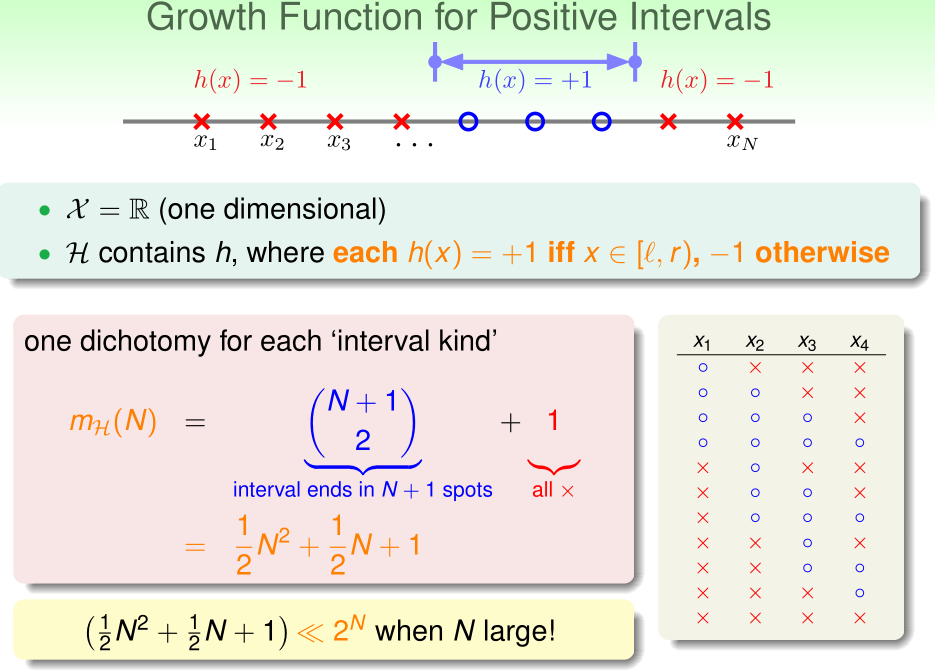
对于由\(h=1 (x\in[L,R]),h=-1(x\notin [L,R])\)构成的集合，\(m_\mathcal H(n)=O(n^2)\ll 2^n\)

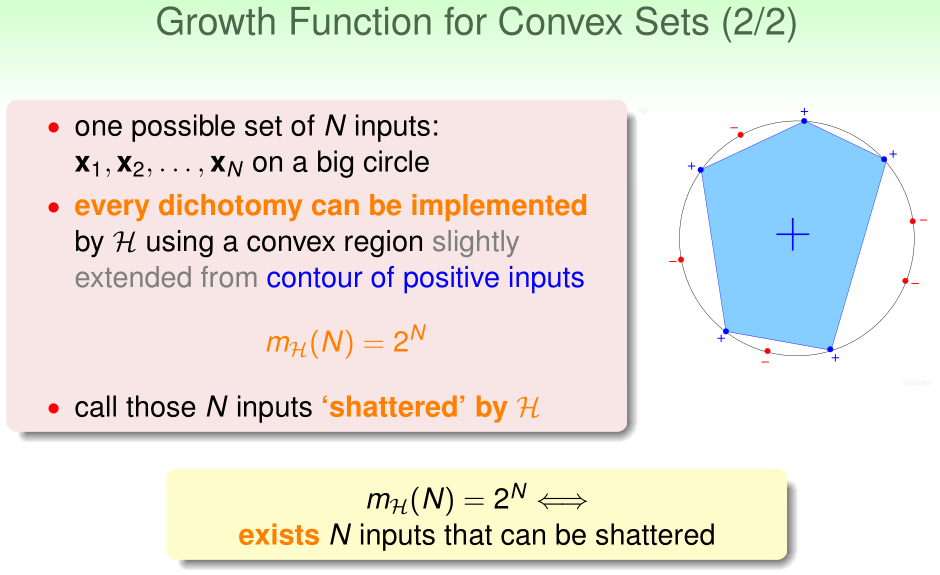
对于n个点分布成一个圈，假设函数为凸多边形区域，此时\(m_\mathcal H(n)=2^n\)，换言之，不论这样的n个点的标签是怎样的，都能找到一个假设函数，使得它们全部被正确分类，我们称这样的n个点可以被\(\mathcal H\) shattered

在前一节中，我们已经知道，n>=3时，一定存在一组\(x^{(1)},\cdots,x^{(n)}\)是不能被任何感知机假设函数正确分类的，表明n>=3时\(m_\mathcal H(n)<2^n\)，我们称满足\(m_\mathcal H(k)<2^k\)的最小的k是break point，或者说，对于任意的k个点都不能被\(\mathcal H\) shattered的最小的k是break point，那么：

• 对于2D感知机算法而言，break point=4(n=3时，取不共线的三个点，这样的三个点可以被shattered)；
• 对于positive rays而言break point=2；
• 对于positive intervals而言break point=3；
• 对于convex sets而言，没有break point(break point=+INF)