机器学习基石(林轩田)学习笔记:Lecture 2 & Lecture 3

Lecture 2: Learning to Answer Yes/No

感知机假设函数集合

假设未知的目标函数为\(f:\mathcal X \mapsto y\)，学习算法\(\mathcal A\)的任务是，根据已有的训练集\(\mathcal D:(x_1,y_1),\cdots,(x_n,y_n)\)，从假设函数集合\(\mathcal H\)中选出最佳的假设函数\(g\)，使得\(g\approx f\)

对于二分类问题：给出输入特征\(x=(x_1,\cdots,x_d)\)，预测其分类\(y\in \{1,-1\}\)，

感知机算法的假设函数可以描述为：

• \(\sum_{i=1}^d w_ix_i>\)阈值t时，假设函数输出分类为1
• \(\sum_{i=1}^d w_ix_i<\)阈值t时，假设函数输出分类为-1

形式化地可以表示为\(h\in \mathcal H\),

\[h(x)=\mathrm{sign}((\sum_{i=1}^d w_ix_i)-t) \]

(x>0时sign(x)=1;x=0时sign(x)=0;x<0时sign(x)=-1,x=0的情况可以忽略)

为了方便表述，我们令\(w_0=-t,x_0=1\)，列向量\(w=(w_0,\cdots,w_d)^T\),\(x=(x_0,\cdots,x_d)^T\),则

\[h(x)=\mathrm{sign}((\sum_{i=1}^d w_ix_i)+(-t)\cdot 1) \]

\[=\mathrm{sign}(\sum_{i=0}^d w_ix_i) \]

\[=\mathrm{sign}(w^Tx) \]

感知机学习算法(Perceptron learning algorithm,PLA)

由于每个参数wi都是实数，因此感知机算法的假设函数集合是无限集。在集合中枚举每个假设函数是不现实的。

感知机学习算法的核心是：随意从某个假设函数\(g_0\)出发，针对它在训练集\(\mathcal D\)上的错误分类，不断修正其参数向量\(w\)

每次，我们从\(\mathcal D\)中找到分类错误的训练样本\((x^{n(t)},y^{n(t)})\)，\(\mathrm{sign}((w^{t})^T x^{n(t)})\neq y^{n(t)}\)，然后作出修正：

\[w^{(t+1)}\gets w^{(t)}+y^{n(t)}x^{n(t)} \]

直到最终假设函数\(g\)在训练集\(\mathcal D\)上没有任何错误分类

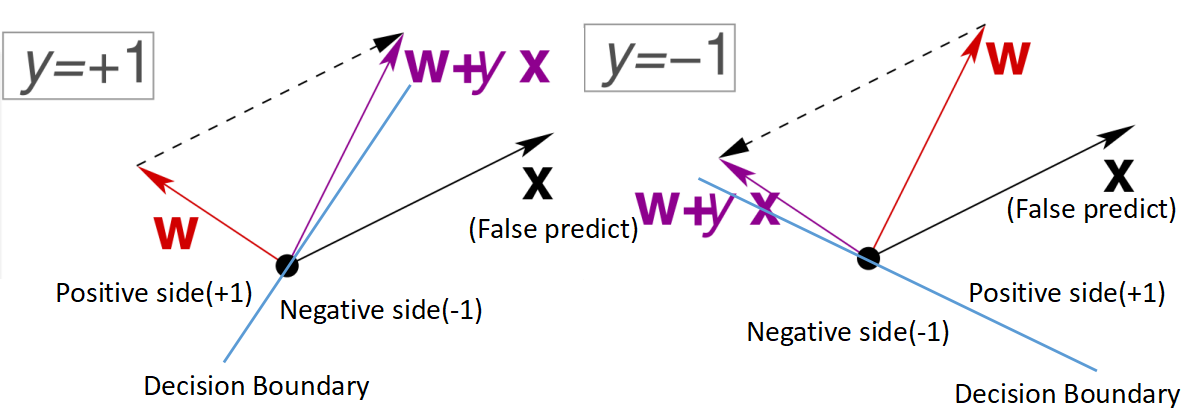
由上图可见，被错误分类的样本x(false predict)的真实标签为y=+1和y=-1时，向量w的变化情况，w会朝着使得这个样本x被正确分类的方向变化。

答案：(3)
证明：根据PLA的参数w的更新公式，\(w_{t+1}=w_t+y_nx_n\)，两边同时转置，并右乘\(x_n\)

\[w_{t+1}^Tx_n=w_t^Tx_n+y_nx_n^Tx_n=w_t^Tx_n+y_n\|x_n\|^2 \]

两边同时乘\(y_n\)

\[y_nw_{t+1}^Tx_n=y_nw_t^Tx_n+y_n^2\|x_n\|^2\geq y_nw_t^Tx_n \]

这一结果表明，随着感知机学习算法的迭代不断进行，它会尝试不断修正每个错误

训练集线性可分情况时的PLA

当训练集\(\mathcal D\)线性可分时，一定存在一个\(w_f\)，使得\(\mathrm{sign}(w_f^Tx_n)\)可以对所有训练样本正确分类。则对于任意的训练样本x，都有\(yw_f^Tx>0\)......(1)

\(y_{n(t)}w_f^Tx_{n(t)}\geq \min_n y_{n}w_f^Tx_{n}>0\)......(2)

对于\(\|w_{t+1}\|\)，我们有：

\[\|w_{t+1}\|^2=\|w_t+y_{n(t)}x_{n(t)}\|^2 \]

\[= \|w_t\|^2+2y_{n(t)}w_t^Tx_{n(t)}+\|y_{n(t)}x_{n(t)}\|^2 \]

\[\leq \|w_t\|^2+0+\|y_{n(t)}x_{n(t)}\|^2 \]

(\((x_{n(t)},y_{n(t)})\)是被错误分类的，所以有\(y_{n(t)}w_t^Tx_{n(t)}<0\))

\[\leq \|w_t\|^2+\max_n \|y_{n}x_{n}\|^2 \]

\[= \|w_t\|^2+\max_n \|x_{n}\|^2 \]

(\(\max_n \|x_{n}\|^2\)是已知常数)

如果初始时参数\(w_{t=0}=0\)，则经过T轮迭代后，对于\(\|w_T\|\)我们有：

\[\|w_T\|^2\leq \|w_{T-1}\|^2+\max_n \|x_{n}\|^2 \]

\[\leq \cdots\leq \|w_{0}\|+T\max_n \|x_{n}\|^2=T\max_n \|x_{n}\|^2 \]

\[\|w_T\|\leq \sqrt T \max_n \|x_{n}\| \]

对于\(w_fw_T\)我们有：

\[w_f^Tw_t=w_f^T(w_{t-1}+y_{n(t-1)}x_{n(t-1)}) \]

\[=w_f^Tw_{t-1}+y_{n(t-1)}w_f^Tx_{n(t-1)} \]

\[\geq w_f^Tw_{t-1}+\min_n y_{n}w_f^Tx_{n} \]

(使用不等式(2))

\[\geq w_f^Tw_{t-2}+2\min_n y_{n}w_f^Tx_{n} \]

\[\geq w_f^Tw_{0}+t\min_n y_{n}w_f^Tx_{n} \]

\[=t\min_n y_{n}w_f^Tx_{n} \]

则\(w_f,w_T\)之间夹角的余弦值

\[\cos(w_f,w_T)=\frac{w_f^T w_T}{\|w_f\|\|w_T\|}\geq \frac {T\min_n y_{n}w_f^Tx_{n}}{\|w_f\|\|w_T\|} \]

\[\geq \frac {T\min_n y_{n}w_f^Tx_{n}}{\|w_f\|\sqrt T \max_n \|x_{n}\|} \]

\[= \frac {\sqrt T\min_n (e^{w_f})\cdot (y_{n}x_{n})}{\max_n \|x_{n}\|} \]

\[\geq C\sqrt T \]

(\(\max_n \|x_{n}\|\)为常量，而\(\forall (x_n,y_n)\in \mathcal D\)，根据不等式(1)，\(y_nx_n \cdot w_f>0\)，另外，显然\(y_nx_n\)与单位向量的内积有下界)

答案：(2)
证明：

\[\frac{\sqrt T\min_n y_nw_f^Tx_n}{\|w_f^T\|\max_n\|x_n\|}\leq \frac{w_f^Tw_T}{\|w_f\|\|w_T\|}=\cos(w_f,w_T)\leq 1 \]

\[\sqrt T\leq \frac{\|w_f^T\|\max_n\|x_n\|}{\min_n y_nw_f^Tx_n} \]

\[T\leq \frac{\|w_f^T\|^2\max_n\|x_n\|^2}{(\min_n y_nw_f^Tx_n)^2} \]

\[T\leq \frac{\max_n\|x_n\|^2}{(\min_n y_n\frac{w_f^T}{\|w_f^T\|}x_n)^2}=\frac{R^2}{\rho^2} \]

这表明，迭代次数T是有上界的

训练集线性不可分情况时的PLA

当训练集线性不可分时，之前的PLA算法会不断循环下去，这时我们可以考虑找到这样的参数\(w_g\):

\[w_g=\arg\min_w \sum_{i=1}^m 1\{y^{(i)}\neq \mathrm{sign}(w^Tx^{(i)})\} \]

然而这个算法是NP-Hard的，并不可行

为了解决这个问题，下面介绍PLA的改进算法：口袋算法(pocket algorithm)

• 初始化口袋参数\(\hat w\)
• for t=0,1,...,MAX-ITERATION{
• ____随机找一个当前的假设函数\(\mathrm{sign}(w^{(t)}x)\)错误分类的训练样本\((x^{n(t)},y^{n(t)})\)
• ____\(w^{(t+1)}:=w^{(t)}+y^{n(t)}x^{n(t)}\)
• ____如果\(w^{(t+1)}\)比\(\hat w\)分类错误率更低，\(\hat w:=w^{(t+1)}\)
• }
• 最终选取的参数为\(\hat w\)

答案:(1)
理由：口袋算法在每次迭代时，都要用训练集D计算一遍\(w^{(t+1)}\)的分类错误率，所以在训练集D线性可分时，速度更慢

Lecture 3: Types of Learning

本讲主要介绍了不同类型的机器学习算法

根据输出\(y\)的不同对机器学习算法分类

根据输出\(y\)的不同，可以将机器学习算法分类为：

• 1、二分类问题(\(y\in\{0,1\}\))
• 2、多分类问题(\(y\in\)大于2个元素构成的集合)
• 3、回归问题(\(y\)是连续值)
• 4、结构化学习(structured learning)(\(y\)是一个结构化的信息)

1、2、3比较常见，而(4)结构化学习算法的输出\(y\)是一个结构，例如输入一个句子，输出它的语法结构：

答案：(2)
理由：由于该问题的输出\(y\in\)包含四个元素的集合，所以是多分类问题。

根据训练集的输出\(y^{(i)}\)的不同对机器学习算法分类

根据训练集的输出\(y^{(i)}\)的不同，可以将机器学习算法分类为：

• 1、监督学习(所有训练样本\(y^{(i)}\)已知)
• 2、无监督学习(所有训练样本\(y^{(i)}\)未知)：例如聚类、密度估计、异常检测等
• 3、半监督学习(部分训练样本\(y^{(i)}\)已知)
• 4、强化学习(不直接给出训练样本\(y^{(i)}\)，只给出每个行为的反馈reward)

答案：(3)
理由：一部分训练样本的\(y^{(i)}\)已知

根据训练数据的提供方式对机器学习算法分类

根据训练数据的提供方式，可以将机器学习算法分类为

• 1、批量学习(batch learning)：一次性将全部训练数据提供给学习算法
• 2、在线学习(online learning)：依次将一个个训练样本提供给学习算法
• 3、主动学习(active learning)：学习算法可以查询对其最有用的未标记样本，并交由人类专家进行标记，再提供给学习算法。

答案：(3)
理由：该学习算法可以主动向人类询问

根据输入特征空间的不同对机器学习算法分类

根据输入特征空间的不同，可以将机器学习算法分类为

• 1、具体特征(concrete features)：输入特征的每个维度都有其具体意义。如判断是否给顾客提供信用卡这一问题中，输入特征的每个维度代表顾客的某种个人信息(收入、欠债情况、工龄等)
• 2、原始特征(raw features)：如数字识别问题中，每个像素点的灰度值是一种特征。有时需要通过特征工程，从原始特征手工提取除具体特征。
• 3、抽象特征(abstract features)：如用户ID等

答案：(4)