CS229 Machine Learning学习笔记:Note 12(强化学习与自适应控制)
强化学习的概念
在监督学习中,我们会给学习算法一个训练集,学习算法尝试使输出尽可能接近训练集给定的真实值y;训练集中,对于每个样本的输入x,都有确定无疑的正确输出y
在强化学习中,我们只会给学习算法一个奖励函数(reward function),用这个函数来提示学习主体(learning agent)什么时候做得好,什么时候做得差。例如,对于一个机器人,当它向前行走时,我们给它奖励(奖励函数值为正),当它摔倒或向后退时,我们给它惩罚(奖励函数值为负)
马尔可夫决策过程(Markov decision processes,MDP)
马尔可夫决策过程是一个元组\((S,A,\{P_{sa}\},\gamma,R)\),其中:
- \(S\)是所有状态构成的集合。(例如,一个直升机的所有可能出现的位置)
- \(A\)是所有动作构成的集合。(例如,对直升机可以进行的所有操作)
- \(\{P_{sa}\}\)是所有的状态转移概率(state transition probability)构成的集合,对于每个\(s\in S,a\in A\),都有一个\(P_{sa}\),\(P_{sa}\)表示当前状态为s,选择操作a以后,转移到的下一个状态的概率分布。
- \(\gamma\in [0,1)\)被称为折扣因子(discount factor),时刻t得到的奖励,要乘上\(\gamma^{t}\),这表明同样的奖励,越早得到,其衰减越少。
- \(R\)是关于状态s和动作a的函数,称为奖励函数(reward function),有时R只与状态s有关。
马尔可夫决策过程是这样进行的:
- 时刻0:我们从状态\(s_0\)开始,选择一个动作\(a_0\in A\);然后,根据\(s_1\sim P_{s_0a_0}\),我们可以随机得到下一步转移到的状态\(s_1\)
- 时刻1:我们选择一个新的动作\(a_1\in A\),根据\(s_2\sim P_{s_1a_1}\),我们可以随机得到下一步转移到的状态\(s_2\)
- ......
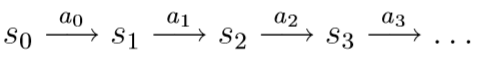
整个过程如上图所示。整个过程中,我们得到的总奖励为
当奖励函数R只与\(s\)有关时,上式可以化简为:
下面我们讨论的是奖励函数R只与\(s\)有关的情况。
在强化学习中,我们的目标是最大化总奖励的期望:
由于\(\gamma\)的衰减作用,我们希望正的奖励值出现得越早越好,负的奖励值出现得越晚越好
策略(policy)函数是一个函数\(\pi:S \mapsto A\),\(\pi(s)\)表示当前状态s时下一步采取的动作,无论何时我们处于状态s,都会采取相同的动作\(a=\pi(s)\)
我们还定义对应于策略\(\pi\)的价值函数为
\(V^\pi(s)\)表示的是,策略函数为\(\pi\),初始状态为s时,得到的总奖励的期望。
当策略函数\(\pi\)固定时,\(V^\pi\)满足Bellman方程:
这表明,\(V^\pi(s)\)由两部分组成:
- 1、当前时刻可以立刻得到的奖励\(R(s)\);
- 2、下一时刻及其未来可以得到的奖励之和的期望,这个和式可以写作\(E_{s'\sim P_{s\pi(s)}}[V^\pi(s')]\)(因为\(s'\)服从分布\(P_{s\pi(s)}\))
有了bellman方程后,我们可以更方便地求出\(V^\pi(s)\)了。在给定\(S,A,\pi,P_{s\pi(s)},R(s)\),状态集是有限集(\(|S|<+\infty\))时,对于每个\(V^\pi(s)\),我们列一个方程,得到\(|S|\)个未知数、\(|S|\)个方程构成的方程组,解出这个方程组即可求出每个\(V^\pi(s)\)
据此,我们进一步还可以定义最优价值函数:
这个函数表示初始状态为s,通过选取最优策略,得到的总奖励的期望的最大值,这个函数的Bellman方程为
等号右侧第一项表示当前时刻可以立刻得到的奖励,第二项表示,当前时刻得到奖励后,选取最优的动作a,下一时刻及其以后得到的奖励的期望的最大值。
根据\(V^*\)的bellman方程,我们可以定义\(\pi^*:S\mapsto A\)
\(\pi^*(s)\)表示状态s时下一步采取的最优动作。
显然,\(\pi^*\)是最优的决策函数,\(V^*\)选择的决策函数就是\(\pi^*\),则有:
这里我们要注意,\(\pi^*\)对于所有状态s而言,都是最优的决策函数。
值迭代与策略迭代
对于已知\(S,A,P_{sa},R(S),\gamma\),且状态数目、决策数目有限的马尔可夫决策过程,我们有两种算法求出\(\pi^*\)
值迭代(value iteration)
- 初始化:所有\(V(s):=0\)
- Repeat until convergence{
- ____对于每个状态\(s\),套用\(V^*\)的bellman方程更新:\(V(s)=R(s)+\max_{a\in A} \gamma \sum_{s'\in S}P_{sa}(s')V(s')\)
- }
这个算法有两种更新方式
- 1、同步更新(synchronous update):将所有的\(V^*(s)=R(s)+\max_{a\in A} \gamma \sum_{s'\in S}P_{sa}(s')V^*(s')\)计算好后,同时将所有\(V(s)\)的值用新值覆盖掉
- 2、异步更新(asynchronous update):对于每个s,计算出\(V^*(s)=R(s)+\max_{a\in A} \gamma \sum_{s'\in S}P_{sa}(s')V^*(s')\)后立刻覆盖掉原来的\(V(s)\)
值迭代若干次后,\(V\)的值将收敛于\(V^*\)的值。这样我们就找到了\(V^*\),我们再用公式\(\pi^*(s)=\arg\max_{a\in A}\sum_{s'\in S}P_{sa}(s')V^*(s')\)求出所有\(\pi^*(s)\)
策略迭代(policy iteration)
- 随机初始化策略函数\(\pi\)
- Repeat until convergence{
- ____(a)令\(V:=V^\pi\)
- ____(b)对于每个状态s,套用\(\pi^*(s)\)的公式,令\(\pi(s):=\arg\max_{a\in A}\sum_{s'\in S}P_{sa}(s')V(s')\)
- }
策略迭代若干次后,\(V\)收敛于\(V^*\),\(\pi\)收敛于\(\pi^*\),这样就可以同时得到\(V^*,\pi^*\),但是很显然,每次迭代的步骤(a)需要解一个|S|个未知数、|S|个方程的线性方程组,计算量太大。因此一般值迭代更常用。
\(P_{sa},R(S)\)未知的马尔可夫决策过程
在大多数情况下,\(S,A,\gamma\)是已知的,但\(P_{sa},R(S)\)是未知的,这两个量需要我们从数据中近似估计。
如果我们已知策略函数\(\pi\),那么我们可以根据策略函数\(\pi\),做T次试验,每次试验,随机初始状态\(s_0^{(i)}\),然后根据策略函数\(\pi\)执行若干步,直至达到终止条件(如倒立摆问题中杆子倒下)
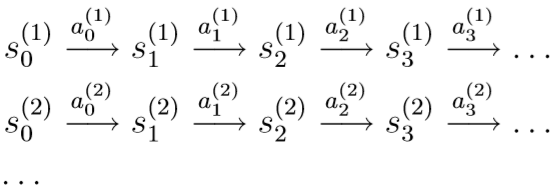
通过这T次试验,我们可以得到\(P_{sa},R(s)\)的近似估计:
\(P_{sa}(s')=\)从状态s采用动作a到达状态s'的次数/在状态s采用动作a的总次数
若\(P_{sa}(s')=0/0\),即,在状态s采用动作a的试验次数为0,这时我们就令\(P_{sa}(s')=1/|S|\),就是假设在状态s,采用动作a到其他任何状态的概率分布,是均匀分布。
类似地,我们也可以对\(R(s)\)近似估计,\(R(s)=\)试验中,在状态s得到的奖励的平均值。
- 随机初始化策略函数\(\pi\)
- Repeat{
- ____(a)根据策略函数\(\pi\)执行若干次试验
- ____(b)使用之前所有的观测数据(不只是本次循环,还有之前所有循环的),估计\(P_{sa},R\)
- ____(c)值迭代,用上一次循环得到的\(V^*\)的估计值,作为本次值迭代的初始的\(V\)的值,最终得到新的\(V^*\)的估计值
- ____(d)用新的\(V^*\)的估计值更新\(\pi\)
- }
这里(c)步用上一次循环得到的\(V^*\)的估计值,可以大大加快每次值迭代的速度。

