CS229 Machine Learning学习笔记:Note 11(独立成分分析ICA)

问题描述

鸡尾酒会问题

在一个酒会上，n个人站在不同的位置同时说话，另外有n个麦克风放在房间不同的位置录音，由于每个麦克风、人的位置不同，所以n个麦克风录下的声音是有差别的。现在要用n个麦克风的录音，还原n个人的说话声音。

建立模型

为了简化问题，我们把某时刻某个声音看作一个实数。令n维列向量\(s^{(i)}\)代表时刻(i)原始n个人说话的声音，实数\(s^{(i)}_j\)表示时刻(i)原始的第j个人说话的声音；n维列向量\(x^{(i)}\)代表时刻(i)时n个麦克风的录音，实数\(x^{(i)}_j\)表示时刻(i)第j个麦克风的录音。

现在，我们得到了若干个时刻的录音数据\(\{x^{(1)},\cdots,x^{(m)}\}\)，目标是要还原每个时刻的原始说话声音\(\{s^{(1)},\cdots,s^{(m)}\}\)

我们用\(x=As\)表示n个人说话声音混在一起，被麦克风录下的过程。矩阵A被称为混合矩阵(mixing matrix)，

最原始的方法

令\(W=A^{-1}\)，我们称之为解混矩阵(unmixing matrix)，只要能求出W，就能通过\(s^{(i)}=Wx^{(i)}\)得到结果。

为了方便表述，令\(w_i^T\)为矩阵W的第i行(\(w_i \in \mathbb R ^n\))。\(W=\begin{pmatrix}-w_1^T-\\\vdots\\-w_n^T-\end{pmatrix}\)

于是时刻i的第j个声音来源\(s_j^{(i)}=w_j^Tx^{(i)}\)

然而在只知道\(\{x^{(1)},\cdots,x^{(m)}\}\)时，这个做法有一系列问题。

• 首先，我们无法区别\(W\)与\(PW\)(P是n阶排列矩阵)，不过这个问题影响不大，求出的是W还是PW，只会导致求出的\(s^{(i)}\)中每个元素的排列顺序不同。

• 其次，我们无法确定每个\(w_i\)的比例(范数的大小)。例如，一种情况下，我们得到了\(W\)和\(s^{(i)}\)，在另一种情况下，我们可能得到的是\(2W\)和\(\frac 1 2 s^{(i)}\)；不仅如此，一种情况下，我们得到了\(w_j,s_j^{(i)}\)，在另一种情况下，我们可能得到了\(\alpha w_j,\frac 1 \alpha s_j^{(i)}\)

• 另外，如果原始声音代表的向量\(s\sim \mathcal N (0,I)\)，此时的\(A\)也是不唯一的。
  假设\(x=As\)，\(\mathrm{Cov}(x)=E[(x-0)(x-0)^T]=E[Ass^TA^T]=AE[ss^T]A^T=AA^T\)
  对于任意一个正交阵R，\(A'=AR\)，\(x'=A's\)，\(\mathrm{Cov}(x')=E[(x'-0)(x'-0)^T]=E[ARss^TR^TA^T]=ARE[ss^T]R^TA^T=AA^T\)
  所以\(A'=AR\)和\(A\)都是合法的。

线性变换对密度函数的影响

在介绍独立成分分析前，先了解一下线性变换对密度函数的影响。

首先看最简单的\(x=As,x\in \mathbb R,s\in \mathbb R\)的情况。注意\(p_x(x)\neq p_s(Wx)(W=A^{-1})\)，比如A=2,\(s\)在区间[0,1]上均匀分布(\(p_s(s)=1(s\in [0,1])\))，则\(p_x(x)=0.5(x\in [0,2])\)

然而如果\(p_x(x)= p_s(Wx)\)，则\(p_x(x)=p_s(Wx)=1\neq 0.5\)，不正确。

正确的式子应为\(p_x(x)= p_s(Wx)|W|\),推广到\(x,s\)是维度相同的向量，变换阵A可逆的情况时，也有\(p_x(x)= p_s(Wx)|W|\)(\(W=A^{-1}\))

ICA算法

下面从最大似然估计的角度来介绍ICA算法

首先假设每个说话人的原始声音\(s_i\)的分布是由密度函数\(p_s\)决定的。那么n个人的原始声音\(s\)的联合分布为：

\[p(s)=\prod_{i=1}^n p_s(s_i) \]

(这里假设n个人的原始声音都是相互独立的)

又\(s=Wx,s_i=w_i^Tx\)，则有

\[p(x)=\prod_{i=1}^n p_s(w_i^Tx)|W| \]

然后我们需要确定每个原始声音的分布的密度函数\(p_s\)

对于实数值的随机变量z而言，其累积分布函数(cumulative distribution function,cdf)\(F\)是\(F(z_0)=P(z\leq z_0)=\int_{-\infty}^{z_0}p_z(z)dz\)，\(p_z(z)=F'(z)\)

为了确定\(p_s\)，首先我们要确定它对应的累积分布函数，累积分布函数是单调递增的，\(F(z)\)随着z增大，函数值由0单调递增到1，这里我们选择Sigmoid函数作为累积分布函数，\(g(s)=\frac 1 {1+e^{-s}}\)，则\(p_s(s)=g'(s)\)

对于大小为m的训练集\(\{x^{(1)},\cdots,x^{(m)}\}\)，我们可以写出关于W的似然函数：

\[L(W)=\prod_{i=1}^m p(x^{(i)})=\prod_{i=1}^m \prod_{j=1}^n p_s(w_j^Tx^{(i)})|W|=\prod_{i=1}^m \prod_{j=1}^n g'(w_j^Tx^{(i)})|W| \]

相应地，对数似然函数

\[l(W)=\sum_{i=1}^m \log (\prod_{j=1}^n g'(w_j^Tx^{(i)})|W|) \]

\[=\sum_{i=1}^m [\sum_{j=1}^n (\log g'(w_j^Tx^{(i)})+\log |W|)] \]

令\(\nabla_Wl=0\)，得到梯度上升算法的W的更新公式为：

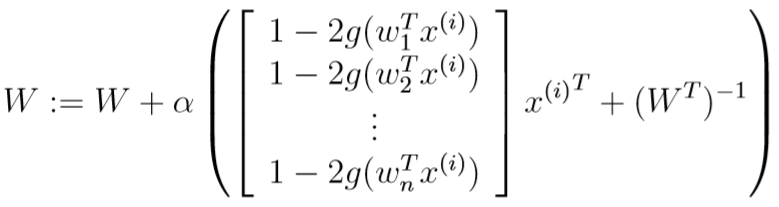
(这里用到了公式\(\nabla_W|W|=|W|(W^{-1})^T\))

实际上，这里的假设\(x^{(i)}\)之间相互独立，往往是不成立的。因为一般\(x^{(i)}\)是连续一段时间上的数据，相邻时刻的数据关联性很强。但我们可以通过随机梯度下降算法，对全体\(x^{(i)}\)随机重新排列(random shuffle)，这样就可以近似地认为\(x^{(i)}\)之间相互独立