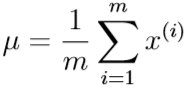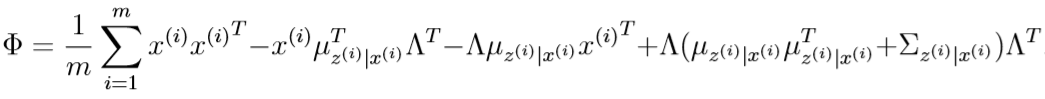CS229 Machine Learning学习笔记:Note 9(因子分析)

问题描述

现在要用多元高斯分布模型拟合若干样本点\(x^{(i)}\in \mathbb R^n\)，但样本特征维数\(n\gg\)样本数\(m\)，此时，求出的协方差矩阵

\[\Sigma_{n\times n}=\frac 1 m (x^{(1)}-\mu,\cdots,x^{(m)}-\mu)(x^{(1)}-\mu,\cdots,x^{(m)}-\mu)^T \]

因为\(r(x^{(1)}-\mu,\cdots,x^{(m)}-\mu)\leq m\)，所以

\[r(\Sigma)\leq \min(r(x^{(1)}-\mu,\cdots,x^{(m)}-\mu),r((x^{(1)}-\mu,\cdots,x^{(m)}-\mu)^T))\leq m<n \]

表明\(\Sigma\)是奇异矩阵，不可逆，而且\(\det \Sigma=0\)，这就导致最终得到的模型是没有意义的。

下面先介绍通过对\(\Sigma\)加入两种约束条件来得到可逆的\(\Sigma\)，然后介绍建立因子分析模型、通过EM算法最大似然估计来得到可逆的\(\Sigma\)

对\(\Sigma\)加入约束条件

如果样本数m太小，我们无法套以往的公式得到可逆的\(\Sigma\)，但是我们可以考虑对\(\Sigma\)加入一些约束条件使其可逆

令\(\Sigma\)为对角阵

令\(\Sigma\)为对角阵，且有

\[\Sigma_{j,j}=\frac 1 m \sum_{i=1}^m (x^{(i)}_j-\mu_j)^2 \]

即对角阵的第j个主对角元是对第j种特征的方差的经验估计(empirical estimate)，其实这种约束就是使多元高斯分布模型还原成了n个相互独立的特征的n个单变量高斯分布模型

从图像上看，这个高斯分布的等高线的轴与坐标轴平行。

这种约束一般可以保证\(\Sigma\)可逆，但还是可能出现某种特征的方差为0，导致\(\Sigma\)变成奇异阵

令\(\Sigma\)为数量阵

我们还可以对\(\Sigma\)作进一步的约束，令其为数量阵(主对角元全部相同的对角阵)：\(\Sigma=\sigma^2 I\)，通过最大似然估计可以得到参数

\[\sigma^2=\frac 1 {mn}\sum_{j=1}^n\sum_{i=1}^m(x_j^{(i)}-\mu_j)^2 \]

\[\mu=\frac 1 m \sum_{i=1}^m x^{(i)} \]

证明如下

注意：以上两种约束，实际上都是在假设n种特征之间相互独立的前提下进行的，因此丢失了数据种一部分有用的信息；现在我们希望利用特征之间的相关性，下面介绍因子分析模型

联合多元高斯分布的条件分布与边缘分布

在介绍因子分析之前，首先介绍联合多元高斯分布，以及如何找到联合多元高斯分布的条件分布与边缘分布。

联合多元高斯分布

假设我们现在有一个随机变量(r+s维列向量)\(x=\begin{pmatrix}x_1\\x_2\end{pmatrix}\),\(x_1\in \mathbb R^r,x_2\in \mathbb R^s\)，我们假设\(x\sim \mathcal N (\mu,\Sigma)\)

其中，

\(\mu=\begin{pmatrix}\mu_1\\\mu_2\end{pmatrix}\)，\(\mu_1\in \mathbb R^r,\mu_2\in \mathbb R^s\)

\(\Sigma=\begin{pmatrix}\Sigma_{11}&\Sigma_{12}\\\Sigma_{21}&\Sigma_{22}\end{pmatrix}\),\(\Sigma_{11}\in \mathbb R^{r\times r}\),\(\Sigma_{12}\in \mathbb R^{r\times s}\),\(\Sigma_{21}\in \mathbb R^{s\times r}\),\(\Sigma_{22}\in \mathbb R^{s\times s}\)

很容易发现，因为\(x\)的均值是\(\mu\)，所以\(x_1\)的均值是\(\mu_1\)，\(E[x_1]=\mu_1\)

而

\[\mathrm{Cov}(x)=\Sigma=\begin{pmatrix}\Sigma_{11}&\Sigma_{12}\\\Sigma_{21}&\Sigma_{22}\end{pmatrix} \]

\[=E[(x-\mu)(x-\mu)^T] \]

\[=E[\begin{pmatrix}x_1-\mu_1\\x_2-\mu_2\end{pmatrix}\begin{pmatrix}x_1-\mu_1\\x_2-\mu_2\end{pmatrix}^T] \]

\[=E\begin{pmatrix}(x_1-\mu_1)(x_1-\mu_1)^T & (x_1-\mu_1)(x_2-\mu_2)^T\\ (x_2-\mu_2)(x_1-\mu_1)^T & (x_2-\mu_2)(x_2-\mu_2)^T \end{pmatrix}\]

第一行\(\Sigma_{11}\)就是\(x_1\)部分的协方差矩阵，与最后一行的矩阵对应起来，可得\(\mathrm{Cov}(x_1)=(x_1-\mu_1)(x_1-\mu_1)^T\),\(E[(x_1-\mu_1)(x_1-\mu_1)^T]=\mathrm{Cov}(x_1)\)

由于联合高斯分布中，某个随机变量的边缘分布也是高斯分布，因此可以得到\(x_1\sim \mathcal N(\mu_1,\Sigma_{11})\)

根据多元高斯分布的性质，若两个变量集是联合高斯分布，那么其中一个集基于另一个变量集上的条件分布，仍为高斯分布，\(x_1|x_2\sim \mathcal N(\mu_{1|2},\Sigma_{1|2})\)，其中

\[\mu_{1|2}=\mu_1+\Sigma_{12}\Sigma_{22}^{-1}(x_2-\mu_2) \]

\[\Sigma_{1|2}=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21} \]

因子分析模型(The Factor analysis model)

首先，我们令隐含随机变量(k维列向量)\(z\in \mathbb R ^k\)

\[z\sim \mathcal N(0,I_k) \]

\[x|z\sim \mathcal N(\mu+\Lambda z,\Psi) \]

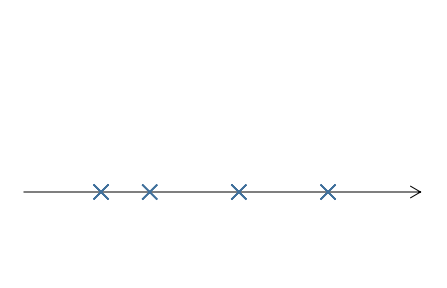
在这个模型中，我们假设每个数据\(x^{(i)}\)，首先是通过一个k维多元高斯分布模型随机生成k维变量\(z^{(i)}\)(图中k=1)

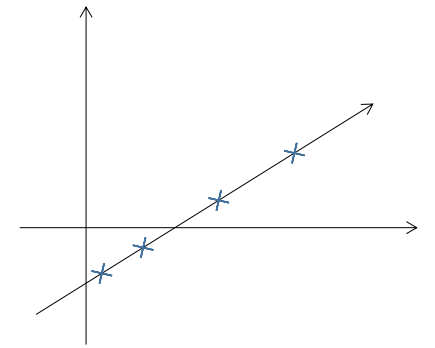
再通过仿射变换\(\mu+\Lambda z^{(i)}\)映射到\(\mathbb R ^n\)向量空间(图中n=2，\(\mu+\Lambda z^{(i)}\)为蓝叉)

最后，通过给\(\mu+\Lambda z^{(i)}\)添加噪声\(\Psi\)得到\(x^{(i)}\)，具体而言，\(x^{(i)}\)是服从以\(\mu+\Lambda z^{(i)}\)为中心，协方差矩阵为\(\Psi\)的多元高斯分布(图中黑叉)

最终生成的\(x^{(i)}\)如图所示

如果我们把\(x^{(i)}\)看作是\(\mu+\Lambda z^{(i)}\)加上一个随机误差\(\epsilon\)，则\(x^{(i)}=\mu+\Lambda z+\epsilon\)，\(\epsilon \sim \mathcal n (0,\Psi)\)

随机变量\(z,x\)服从联合高斯分布：

\[\begin{pmatrix}z\\x\end{pmatrix}\sim \mathcal N(\mu_{zx},\Sigma) \]

由于\(z\)均值为0，而

\[E[x]=E[\mu+\Lambda z+\epsilon]=\mu+\Lambda E[z]+E[\epsilon]=\mu \]

所以x均值为\(\mu\)

从而有\(\mu_{zx}=\begin{pmatrix}0\\\mu\end{pmatrix}\)

然后我们计算\(\Sigma\)，首先，显然\(\Sigma_{zz}=\mathrm{Cov}(z)=I\)

再计算\(\Sigma_{zx}\)：

\[\Sigma_{zx}=E[(z-E[z])(x-E[x])^T] \]

\[=E[z(\mu+\Lambda z+\epsilon-\mu)^T] \]

\[=E[z(\Lambda z+\epsilon)^T] \]

\[=E[z(z^T \Lambda^T+\epsilon^T)] \]

\[=E[zz^T]\Lambda^T+E[z \epsilon^T] \]

\[=\mathrm{Cov}(z)\Lambda^T+E[z]E[\epsilon^T] \]

(\(z,\epsilon\)相互独立，期望可以拆开)

\[=\Lambda^T \]

(Cov(z)=I)

类似地，可以求出\(\Sigma_{xx},\Sigma_{xz}\)

最终得到\(\Sigma\)：

\[\Sigma=\begin{pmatrix}I&\Lambda^T\\\Lambda&\Lambda\Lambda^T+\Psi\end{pmatrix} \]

\(\begin{pmatrix}z\\x\end{pmatrix}\)的高斯分布模型为：

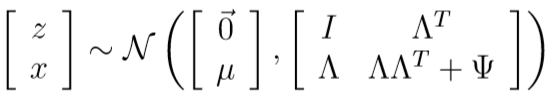
根据\(\mu_{zx}\)和\(\Sigma\)可见，\(x\)的边缘分布\(x\sim \mathcal N(\mu,\Lambda\Lambda^T+\Psi)\)

则似然函数和对数似然函数分别为：

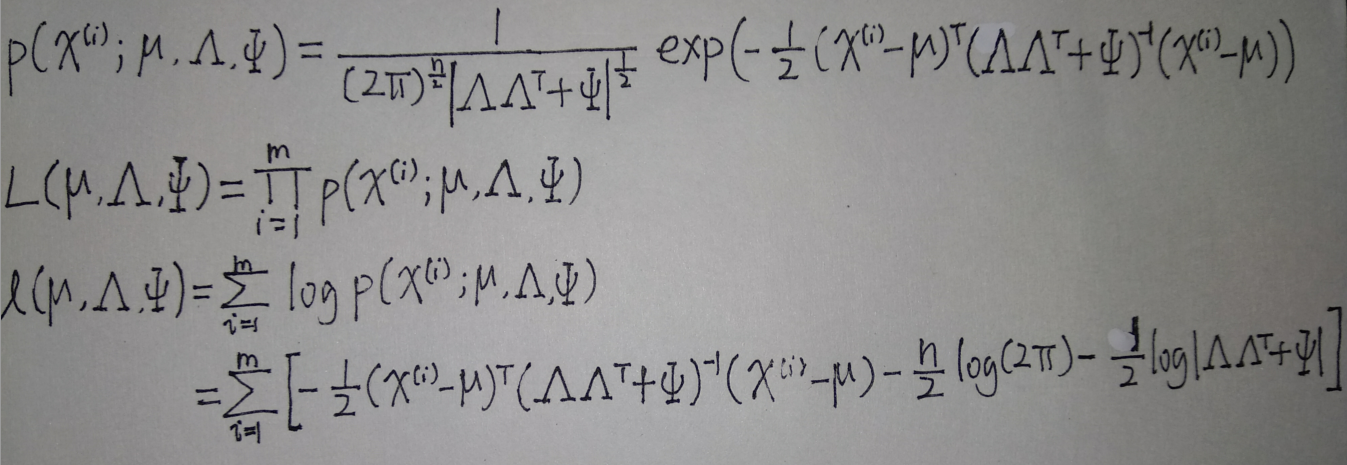
如果直接最大化这个对数似然函数，我们无法得到参数\(\mu,\Lambda,\Psi\)的封闭解(解析解)，下面介绍用EM算法最大化对数似然函数

因子分析的EM算法

和Note 8的EM算法类似，在E-step中，我们先求出\(Q_i\)：

\[Q_i(z^{(i)})=p(z^{(i)}|x^{(i)};\mu,\Sigma,\Psi) \]

之前我们已经说过，在给出\(x^{(i)}\)的条件下\(z^{(i)}\)服从多元高斯分布：

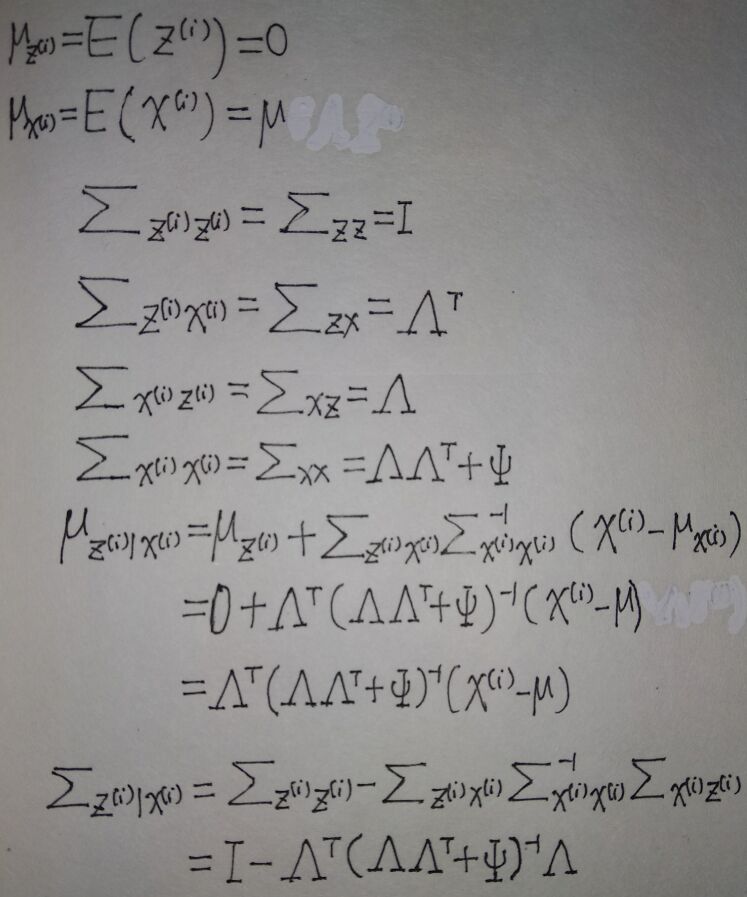
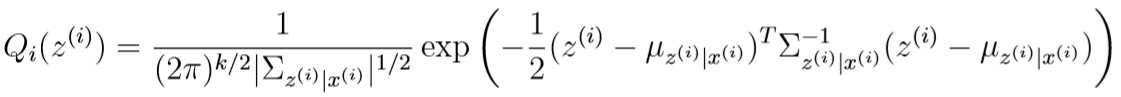
然后开始M-step，跟Note 8差不多，我们需要最大化关于参数\(\mu,\Lambda,\Psi\)的值，注意这里\(z^{(i)}\)是连续值，所以是积分式，而不是和式

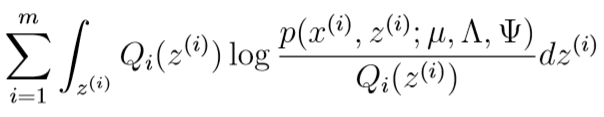
(因为很明显\(z^{(i)}\sim Q_i\)，后面为了方便表述会把这个下标省去)

去掉其中与参数无关的部分后，要最大化的式子变成了

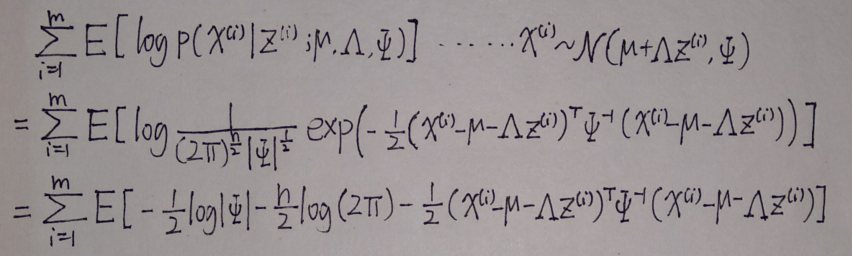
该式子对\(\Lambda\)求向量微分

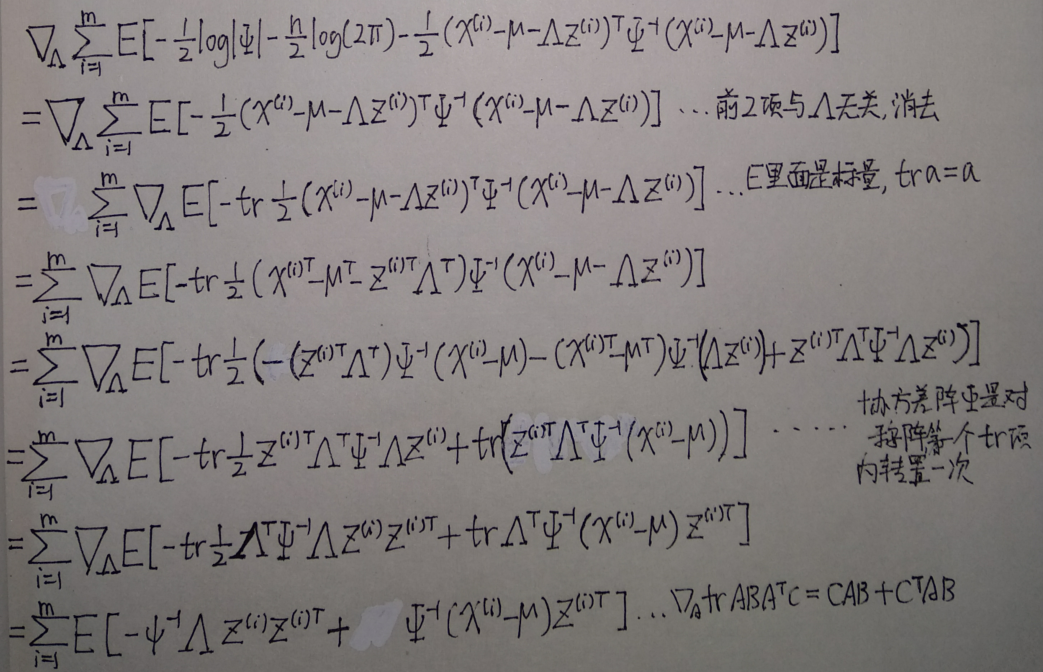
令其等于0，得到

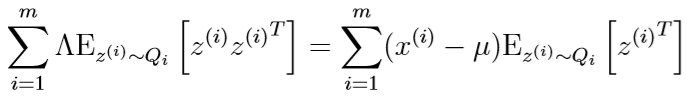
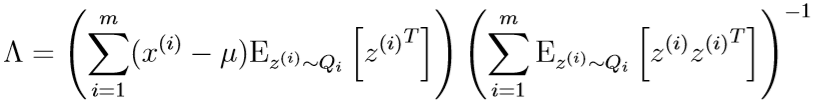
之前我们已经证明了，\(Q_i\)是均值为\(\mu_{z^{(i)}|x^{(i)}}\)，均方差为\(\Sigma_{z^{(i)}|x^{(i)}}\)的多元高斯分布。

对于随机列向量Y，其协方差矩阵

\[\mathrm{Cov}(Y)=E[(Y-E[Y])(Y-E[Y])^T] \]

\[=E[YY^T-E[Y]Y^T-Y(E[Y])^T+E[Y](E[Y])^T] \]

\[=E[YY^T]-E[Y]E[Y^T]-E[Y](E[Y])^T+E[Y](E[Y])^T \]

E[Y]是常量(Y的均值)，所以E[Y]=Y

\[=E[YY^T]-E[Y](E[Y])^T \]

从而有：\(E[YY^T]=E[Y](E[Y])^T+\mathrm{Cov}(Y)\)

套用这个公式可得

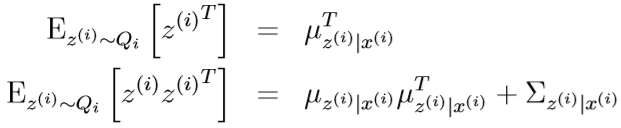
代入到之前的式子里，得到\(\Lambda\)的更新公式：

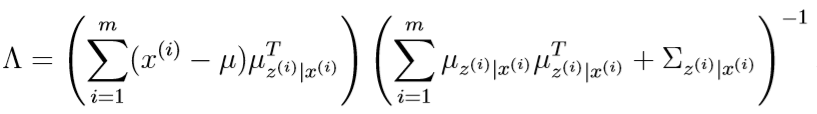
类似地，也可以求出\(\mu,\Psi\)的更新公式：