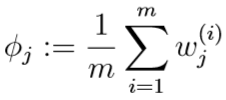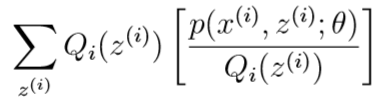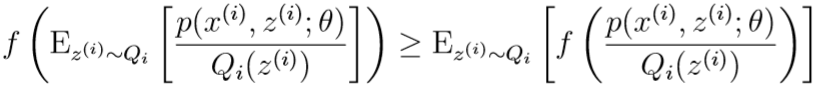CS229 Machine Learning学习笔记:Note 8(EM算法)

琴生不等式(Jensen's inequality)

对于函数\(f(x)\in \mathbb R(x\in \mathbb R)\)，当\(f''(x)\geq 0\)时，f(x)为凸函数，当\(f''(x)> 0\)时，f(x)为严格凸函数

若把自变量x换成向量，则当f的hessian矩阵H半正定(记作\(H\geq 0\))时，f(x)是凸函数，当f的hessian矩阵H正定时(记作\(H>0\))，f(x)是严格凸函数

琴生不等式： 设f是一个凸函数，X是随机变量(标量或向量)，则有：

\[E[f(X)]\geq f(E[X]) \]

• 如果f是严格凸函数，则当且仅当X=E[X]的概率为1(例如X是常数)时，\(E[f(X)]= f(E[X])\)

• E[X]也可简写为EX

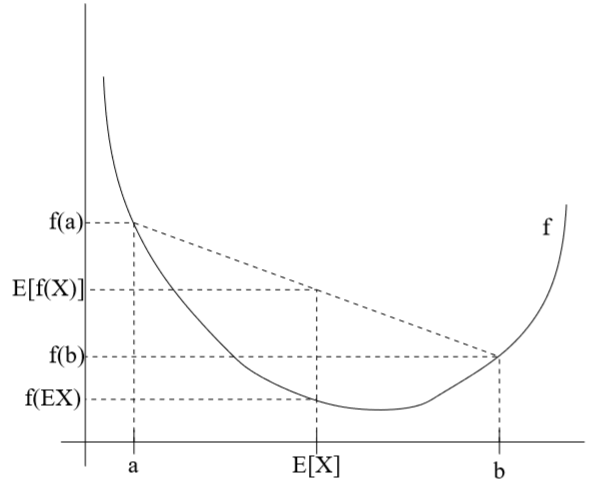
例如对于上图的凸函数f(x),随机变量\(X\in\{a,b\}\)，\(p(X=a)=p(X=b)=0.5\)，则\(E[X]=0.5a+0.5b=\frac 1 2 (a+b)\)，同样地，\(E[f(X)]=0.5f(a)+0.5f(b)=\frac 1 2 (f(a)+f(b))\)，从图中可见\(E[f(X)]\geq E[X]\)

相反地，若f(x)是凹函数，则-f(x)是凸函数，对-f(x)运用琴生不等式可得\(E[f(X)]\leq f(E[X])\)

问题简化后的EM算法

先考虑简化过的情况。假设给定训练集\(\{x^{(1)},\cdots,x^{(m)}\}\)，其中m个样本之间相互独立。现在要用模型\(p(x,z)\)(z是隐含随机变量，\(z^{(i)}\)表示\(x^{(i)}\)所属类别)对这些数据拟合，关于\(\theta\)的对数似然函数为：

\[l(\theta)=\sum_{i=1}^m \log p(x;\theta)=\sum_{i=1}^m\log\sum_{z}p(x,z;\theta) \]

在Note 7中已经提到过，直接最大化这个对数似然函数很难，如果给定了所有\(z^{(i)}\)，最大化这个函数就很容易了。

而EM算法可以有效地最大化上面的对数似然函数，其核心是重复进行两个步骤：

• (1)通过琴生不等式确定对数似然\(l\)的下限，并通过构造\(Q_i\)(\(x^{(i)}\)的标签\(z^{(i)}\)的概率分布)使不等式两边取等，换言之，找到使对数似然取值最小的\(Q_i\)(E-step)
• (2)更新参数\(\theta\)，让这个下限变大(M-step)

对于每个训练样本\(x^{(i)}\)，令\(Q_i\)为\(x^{(i)}\)的标签\(z^{(i)}\)的概率分布，根据概率分布函数的特点，有：\(\sum_{z}Q_i(z)=1,Q_i(z)\geq 0\)

对数似然函数\(l(\theta)\)=

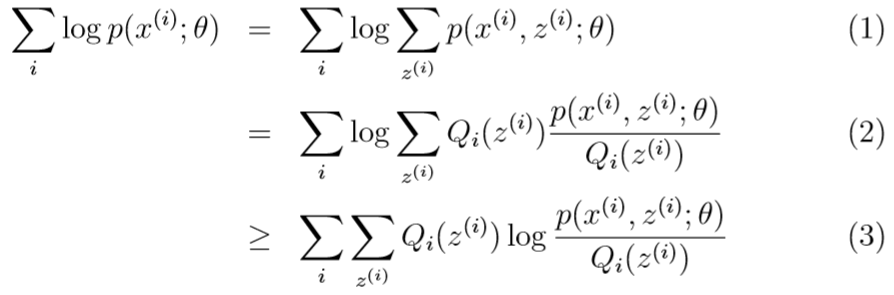
其中从(2)到(3)运用了琴生不等式：此处\(f(x)=\log x\)

这一项可以视为\([p(x^{(i)},z^{(i)};\theta)/Q_i(z^{(i)})]\)的期望\(E_{z^{(i)}\sim Q_i}[\cdot]\)
根据琴生不等式，有：

不等式(3)告诉我们，在给定每个\(z^{(i)}\)的分布\(Q_i\)后，关于\(\theta\)的对数似然函数的取值的下限

为了让不等式(3)取等号，根据琴生不等式的取等条件，这里要令被计算期望的\([p(x^{(i)},z^{(i)};\theta)/Q_i(z^{(i)})]\)是一个常数c(c与\(z^{(i)}\)无关)：

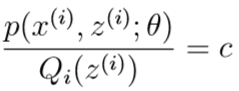
此时\(Q_i(z^{(i)})\)与\(p(x^{(i)},z^{(i)};\theta)\)成比例，而之前根据概率分布的性质，我们知道\(\sum_{z}Q_i(z)=1\)，

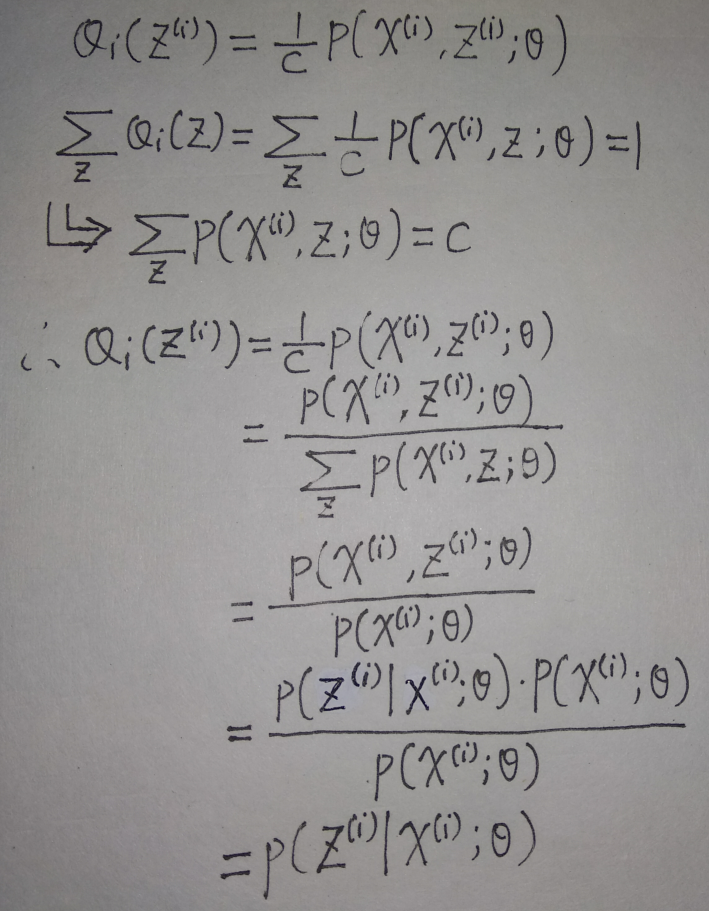
所以，我们只要令\(Q_i(z^{(i)})=p(z^{(i)}|x^{(i)};\theta)\)，即在\(x^{(i)}\)的条件下，\(z^{(i)}\)的后验分布，即可使得琴生不等式左右两边取等。

问题简化后的EM算法可以描述为：

Repeat until convergence{
____(E-step)For each i,令\(Q_i(Z^{(i)})=p(z^{(i)}|x^{(i)};\theta)\)
____(M-step)更新参数：\(\theta:=\arg \max_\theta \sum_i\sum_{z^{(i)}} Q_i(z^{(i)})\log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i{z^{(i)}}}\)
}

证明：上述算法能保证每次迭代都使对数似然函数值增大

假设第t,t+1次迭代后的参数分别为\(\theta^{(t)},\theta^{(t+1)}\)，下面证明\(l(\theta^{(t)})\leq l(\theta^{(t+1)})\)

第t次迭代后，现在到了第t+1次迭代：我们取\(Q_i^{(t)}(z^{(i)})=p(z^{(i)}|x^{(i)};\theta^{(t)})\)，此时不等式(3)取等

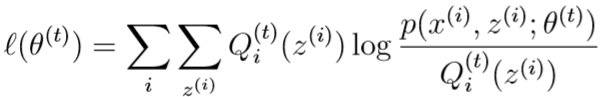......(7)

再次用不等式(3):

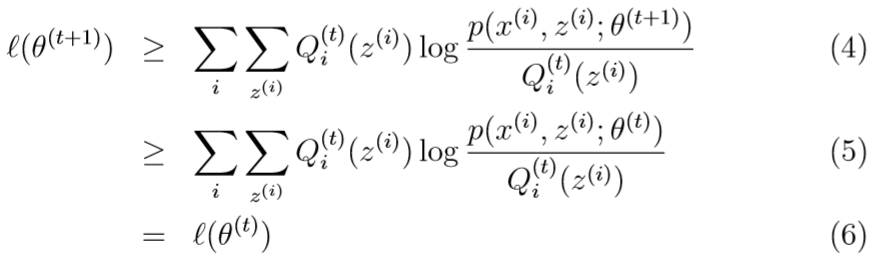
其中，不等式(4)用到了之前的不等式(3)，(4)到(5)是根据第t+1次迭代的M-step的更新规则\(\theta:=\arg \max_\theta \sum_i\sum_{z^{(i)}} Q_i(z^{(i)})\log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i{z^{(i)}}}\)，(5)到(6)是根据这一堆不等式上面的式(7)

高斯混合模型的EM算法

E-step: 与之前问题简化过的EM算法差不多，\(w_j^{(i)}=Q_i(z^{(i)}=j)=p(z^{(i)}=j|x^{(i)};\theta,\mu,\Sigma)\)，其中\(Q_i(z^{(i)}=j)\)表示在\(Q_i\)分布下，第i个样本分类为j的概率

M-step: 在确定了\(z^{(i)}\)的分布\(Q_i\)后，最大化关于\(\phi,\mu,\Sigma\)的量：

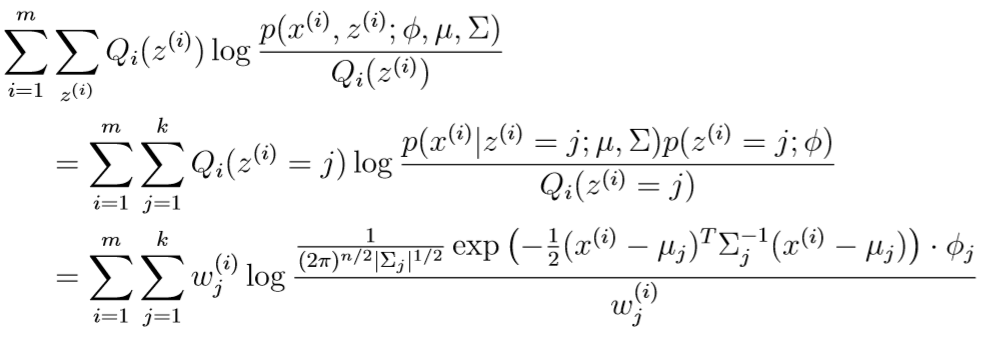
例如，求出这个式子对参数\(\mu_l\)的偏导：

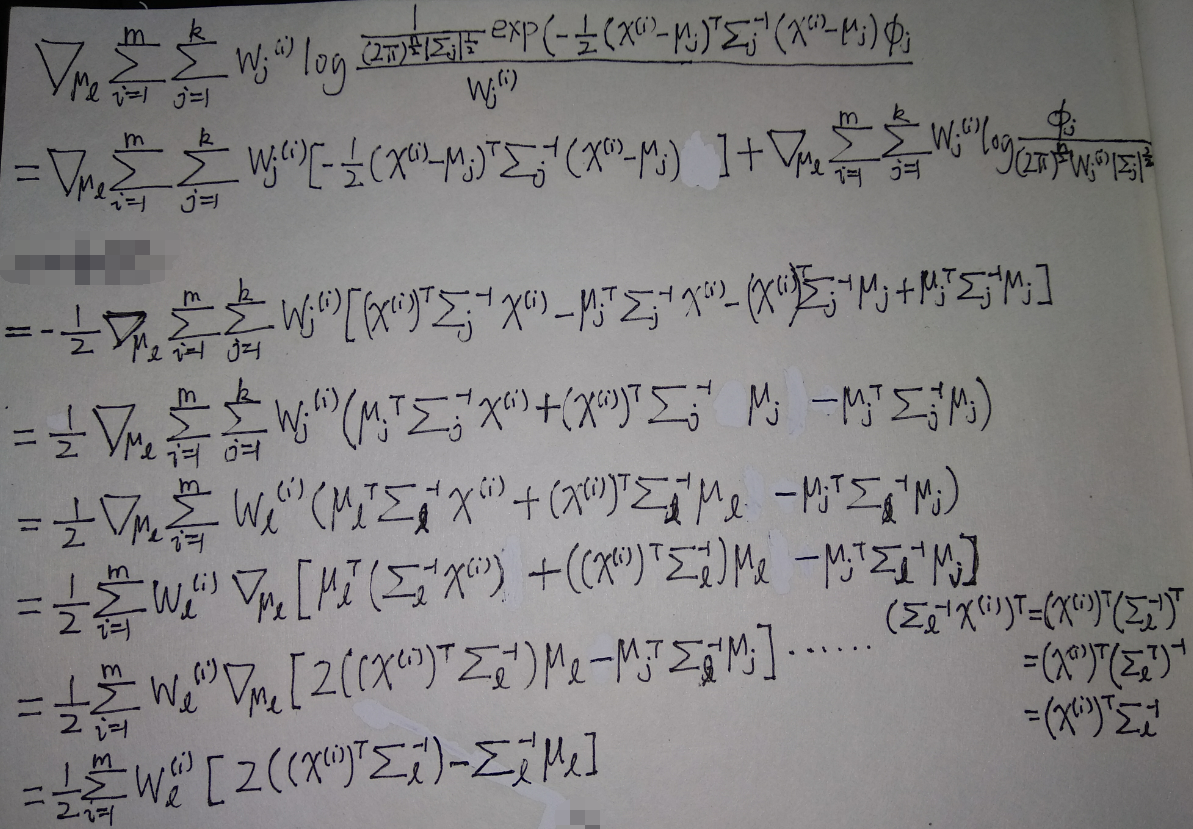
并令其等于0，得到新的\(\mu_l\)

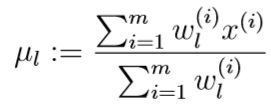
再举一例：求出新的\(\phi_j\)，在原式中去掉与\(\phi_j\)无关的部分，可以发现优化目标等价于：

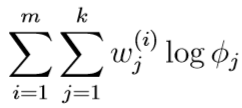
但是这个优化目标有约束条件\(\sum_{j=1}^k \phi_j=1\)(因为\(\phi_1,\cdots,\phi_k\)是多项式分布的参数，\(\phi_j=p(z^{(i)}=j;\phi)\))，因此我们要构造拉格朗日函数：

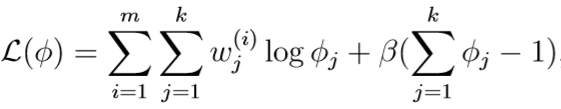
其中\(\beta\)是拉格朗日乘子，拉格朗日函数对\(\phi_j\)求偏导：

\[\frac \partial {\partial \phi_j}\mathcal L(\phi)=\sum_{i=1}^m \frac{w_j^{(i)}}{\phi_j}+\beta \]

令其等于0，解得：

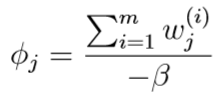
又因为\(\sum_{j=1}^k \phi_j=1\)，所以：
\(\sum_{j=1}^k \phi_j=-\sum_{j=1}^k \frac{\sum_{i=1}^m w_j^{(i)}}{\beta}=1\)，\(-\beta=\sum_{j=1}^k\sum_{i=1}^m w_j^{(i)}=\sum_{i=1}^m\sum_{j=1}^k w_j^{(i)}\)

又\(w_j^{(i)}=Q_i(z^{(i)}=j)\),\(\sum_{j=1}^k w_j^{(i)}=1\)，所以\(-\beta=\sum_{i=1}^m 1=m,\beta=-m\)，代入上式得：