CS229 Machine Learning学习笔记:Note 7(K-means聚类、高斯混合模型、EM算法)

K-means聚类

ng在coursera的机器学习课上已经讲过K-means聚类，这里不再赘述

高斯混合模型

问题描述

聚类问题：给定训练集\(\{x^{(1)},\cdots,x^{(m)}\}\)，每个数据没有任何标签。这是一个无监督学习问题

模型描述

首先，我们认为每个数据所属的类别满足一定的概率分布。定义隐含随机变量(latent random variable)\(z^{(1)},\cdots,z^{(m)}\)，随机变量\(z^{(i)}\)代表了第i个数据\(x^{(i)}\)所属的类别。

每个\(z^{(i)}\in\{1,\cdots,k\}\)，\(z^{(i)}\sim \mathrm{Multinomial}(\phi)\)，即每个\(z^{(i)}\)服从由参数\(\phi_1,\cdots,\phi_k\)决定的多项式分布，\(p(z^{(i)}=j)=\phi_j\)，\(\sum_{j=1}^k \phi_j=1\)

另外，我们认为对于k个不同的标签，相对应有k个不同的多元高斯分布。在已知\(x^{(i)}\)所属类别\(z^{(i)}=j\)后，\(x^{(i)}\)服从其类别\(j\)对应的多元高斯分布：\((x^{(i)}|z^{(i)}=j)\sim \mathcal N (\mu_j,\Sigma_j)\)；进一步，我们可以得到\(x^{(i)},z^{(i)}\)的联合分布：

\[p(x^{(i)},z^{(i)})=p(x^{(i)}|z^{(i)})p(z^{(i)}) \]

整个模型可以描述为：对于每个样本\(x^{(i)}\)，首先根据多项式分布随机生成其标签\(z^{(i)}\)(隐含随机变量)，然后根据标签\(z^{(i)}\)对应的多元高斯分布模型随机生成该样本\(x^{(i)}\)

该模型关于\(\phi,\mu,\Sigma\)的似然函数为：

\[\mathcal L(\phi,\mu,\Sigma)=\sum_{i=1}^m p(x^{(i)};\phi,\mu,\Sigma) \]

\[=\sum_{i=1}^m\sum_{j=1}^k p(x^{(i)}|z^{(i)}=j;\mu_j,\Sigma_j)p(z^{(i)}=j;\phi_j) \]

相应地，对数似然函数为：

\[l(\phi,\mu,\Sigma)=\sum_{i=1}^m \log p(x^{(i)};\phi,\mu,\Sigma) \]

\[=\sum_{i=1}^m\log[\sum_{j=1}^k p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)] \]

这个式子不能通过令对数似然函数\(l\)对各个参数的偏导数=0来求得最优解。

但如果我们已知每个样本的标签\(z^{(i)}=j\)的话，即，\(p(z^{(i)}\neq j;\phi)=0\)，此时对数似然函数可以简化为

\[l(\phi,\mu,\Sigma)=\sum_{i=1}^m\log[p(x^{(i)}|z^{(i)};\mu,\Sigma)p(z^{(i)};\phi)] \]

\[l(\phi,\mu,\Sigma)=\sum_{i=1}^m[\log p(x^{(i)}|z^{(i)};\mu,\Sigma)+\log p(z^{(i)};\phi)] \]

此时再对各参数求偏导,并令偏导函数=0，得到各参数取值：

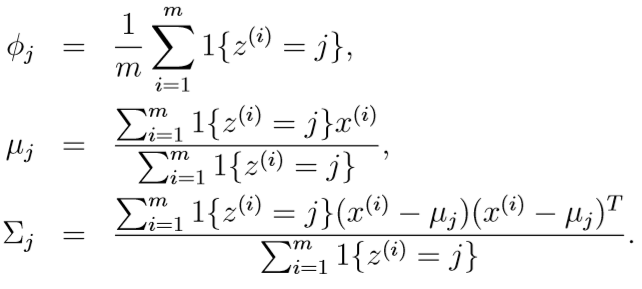
此时各参数的式子和高斯判别分析模型非常相似，但如果现在不知道每个样本的分类\(z^{(i)}\)，就需要另一种算法：EM算法

EM(Expectation-Maximization)算法

Repeat until convergence{
____(E-step)
____For each i,j:
________令\(w_j^{(i)}:=p(z^{(i)}=j|x^{(i)};\phi,\mu,\Sigma)\)
____(M-step)更新各个参数
____\(\phi_j:=\frac 1 m \sum_{i=1}^m w_j^{(i)}\)
____\(\mu_j:=\frac{\sum_{i=1}^m w_j^{(i)}x^{(i)}}{\sum_{i=1}^m w_j^{(i)}}\)
____\(\Sigma_j:=\frac {\sum_{i=1}^m w_j^{(i)}(x^{(i)}-\mu_j)(x^{(i)}-\mu_j)^T}{\sum_{i=1}^m w_j^{(i)}}\)
}

可见，这里用更"软"的\(w_j^{(i)}\)替代了原有的\(1\{z^{(i)}=j\}\)，其中：

\(p(z^{(i)}=j|x^{(i)};\phi,\mu,\Sigma)\)是在给定\(x^{(i)}\)的条件下\(z^{(i)}=j\)的后验概率，根据贝叶斯公式有：

\[p(z^{(i)}=j|x^{(i)};\phi,\mu,\Sigma)=\frac{p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{p(x^{(i)})} \]

\[=\frac{p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{\sum_{l=1}^k p(x^{(i)}|z^{(i)}=l;\mu,\Sigma)p(z^{(i)}=l;\phi)} \]

\(p(x^{(i)}|z^{(i)}=l;\mu,\Sigma)\)是在标签\(l\)对应的多元高斯分布模型中，\(x^{(i)}\)的概率

根据最开始的假设\(z^{(i)}\)服从多项式分布，\(p(z^{(i)}=l;\phi)=\phi_l\)