CS229 Machine Learning学习笔记:Note 3(支持向量机、SMO算法)

在逻辑回归中，对于输入特征\(x\)，\(|\theta^Tx|\)越是大于0，则分类结果为0(1)的置信度将越大。所以要让决策边界离正负样本的距离尽可能远，这就是SVM的motivation

符号约定

为方便描述，样本标签\(y\in\{-1,1\}\)，而非之前的{0,1}，并单独表示偏置\(b\)，使得参数\(w\)为n维列向量(而非之前的n+1维列向量)，输入特征x也为n维列向量(去掉了\(x_0=1\)这一项)，则假设函数可以表示为：

\[h_{w,b}(x)=g(w^Tx+b) \]

注意这里的\(g(z)\)当\(z\geq 0\)时为1，否则为-1,这样做就跳过了得到\(p(y=1|x)\)的中间过程

函数边界(Functional Margin)

令训练样本为\((x^{(i)},y^{(i)})\)，则由参数\((w,b)\)决定的，训练样本i对应的函数边界为：

\[\hat \gamma^{(i)}=y^{(i)}(w^Tx+b) \]

为了让训练样本离决策边界尽可能远，在\(y^{(i)}=1\)时，我们希望\(w^Tx+b \gg 0\)，\(y^{(i)}=-1\)时，我们希望\(w^Tx+b \ll 0\)，即，要让函数边界\(\hat \gamma^{(i)} \gg 0\)

而由之前假设函数里的\(g(z)\)的定义可知，\(g(z)=g(2z)\)，则\(g(w^Tx+b)=g(2w^Tx+2b)\)，所以为了让函数边界更大，可以用\((2w,2b)\)代替\((w,b)\)，然而这种放大倍数是毫无意义的，没有改变决策边界。所以这里强制要求\(\|w\|_2=1\)

对应于一个训练集\(S\)的函数边界就是:

\[\hat \gamma=\min_{i=1,\cdots,m}\hat \gamma^{(i)} \]

几何边界(Geometric Margin)

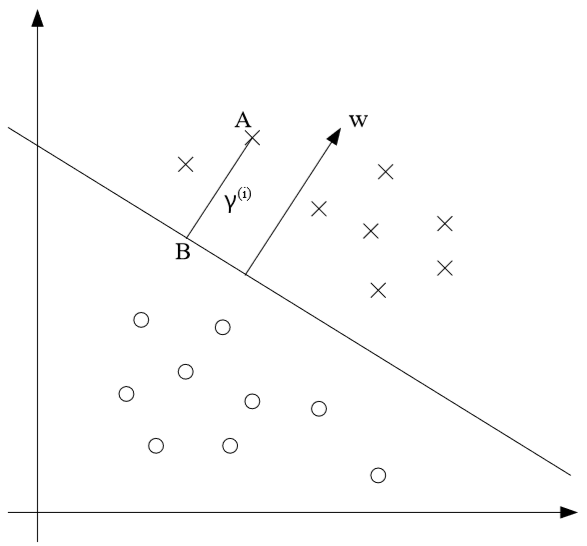
训练样本i的几何边界\(\gamma^{(i)}\)是\(x^{(i)}\)到决策边界的距离。如图所示(X为正样本y=1，O为负样本y=-1)

\(y^{(i)}=1\)时，注意到向量\(w\)垂直于决策边界\(w^Tx+b=0\),则\(x^{(i)}\)到决策边界的投影点可以表示为：

\[x^{(i)}-\gamma^{(i)}\frac w {\|w\|} \]

该点在决策边界上，满足\(w^Tx+b=0\)，则

\[w^T(x^{(i)}-\gamma^{(i)}\frac w {\|w\|})+b=0 \]

解得

\[\gamma^{(i)}=\frac 1 {\|w\|}(w^Tx^{(i)}+b) \]

\(y^{(i)}=-1\)时，类似的有

\[\gamma^{(i)}=-\frac 1 {\|w\|}(w^Tx^{(i)}+b) \]

综上可得

\[\gamma^{(i)}=\frac {y^{(i)}} {\|w\|}(w^Tx^{(i)}+b) \]

对训练集S而言，

\[\gamma=\min_{i=1,\cdots,m}\gamma^{(i)} \]

注意到，当存在约束条件\(\|w\|_2=1\)时，\(\gamma^{(i)}=\hat\gamma^{(i)}\)

SVM的优化目标

假定现在的训练集是线性可分的，SVM需要最大化决策边界与正、负样本之间的间隔，即最大化几何间隔\(\gamma\)，优化目标为：

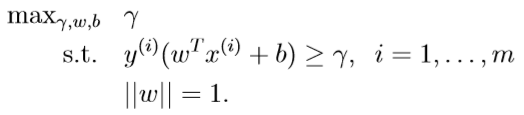
即，在满足每个样本被正确分类，且到决策边界的距离大于\(\gamma\)的前提下，最大化几何间隔，而约束条件里的\(\|w\|=1\)则保证了\(\gamma=\hat\gamma\)，但这个约束条件不方便凸优化，优化目标需要改写为：

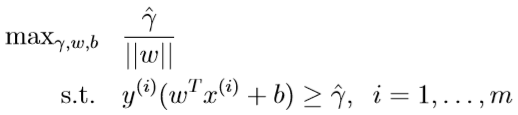
由于参数\((w,b)\)对应于\(\hat \gamma\)时，参数\((kw,kb)\)对应于\(k \hat \gamma\)，二者是等价的，所以如果上面的优化目标求出的解是\((w,b)\)，在强制令\(\hat \gamma=1\)时，也能求得等价的参数\((kw,kb)\)

因此，优化目标中可以令\(\hat \gamma=1\)，则\(\max_{\gamma,w,b}\frac{\hat \gamma}{\|w\|}\)转化为\(\max_{\gamma,w,b}\frac{1}{\|w\|}\)，这等价于\(\min_{\gamma,w,b} \|w\|\)，进一步，等价于\(\min_{\gamma,w,b}\frac{1}2 \|w\|^2\)

从而，优化目标等价于：

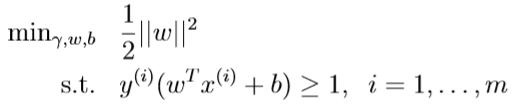
拉格朗日对偶问题(Lagrange duality)

拉格朗日乘数法

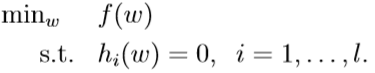
对于上面这个最优化问题，约束条件为l个等式，则可以通过拉格朗日乘数法构造拉格朗日函数：

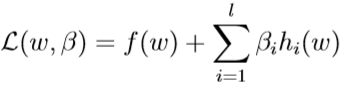
令\(\mathcal L(w,\beta)\)对各个参数的偏导数为0，就能求出\(w,\beta\)：

\[\frac{\partial \mathcal L}{\partial w_i}=0,\frac{\partial \mathcal L}{\partial \beta_i}=0 \]

广义拉格朗日函数(Generalized Lagrangian)

对于下面这个最优化问题，我们称之为原始优化问题(Primal Optimization Problem)

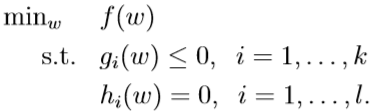
该问题有k个不等式约束条件，l个等式约束条件

构造广义拉格朗日函数

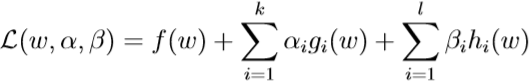
其中的\(\alpha_i,\beta_i\)都是拉格朗日乘子

再定义关于w的函数\(\theta_{\mathcal P}(w)\)(P代表原始(primal)):

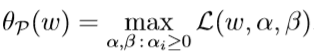
表示给定w，且有约束条件\(\alpha_i\geq 0\)的情况下\(\mathcal L (w,\alpha,\beta)\)的最大值。

则：

• 1.给定的\(w\)不满足原始问题的某些约束条件。

如果存在\(g_i(w)>0\)，取\(\alpha_i=+\infty\)，则\(\theta_{\mathcal P}(w)=+\infty\)

如果存在\(h_i(w)>0(<0)\)，取\(\alpha_i=+\infty(-\infty)\)，则\(\theta_{\mathcal P}(w)=+\infty\)

• 2.给定的\(w\)满足原始问题的全部约束条件

如果对于给定的\(w\)，\(g_i(w)< 0\),则\(\alpha_i=0,\alpha_ig_i(w)=0\)(否则\(\alpha_i>0,\alpha_ig_i(w)<0\)，\(\theta_{\mathcal P}(w)\)取不到最大值)

若\(g_i(w)= 0\),则\(\alpha_ig_i(w)=0\)

若\(h_i(w)=0\)，则\(\beta_ih_i(w)=0\)

所以若给定的\(w\)满足原始问题的全部约束条件时，\(\theta_{\mathcal P}(w)=f(w)\)；反之，不满足某些原始约束条件时，该函数取值为\(+\infty\)：

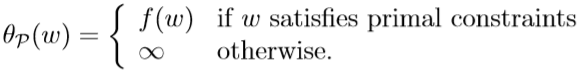
所以，优化问题：

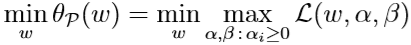
等价于之前的原始优化问题，因为这里的\(\theta_{\mathcal P}(w)\)起到了排除不满足原始约束条件的\(w\)的作用。

我们令\(p^*=\min_w \theta_{\mathcal P}(w)\)为原始问题的最优值。

定义关于\(w\)的函数\(\theta_{\mathcal D}(\alpha,\beta)\)(D代表对偶(dual))

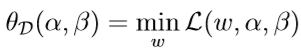
原始优化问题的对偶问题为：

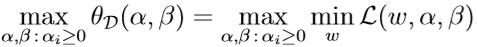
令\(d*=\max_{\alpha,\beta:\alpha_i\geq 0}\theta_{\mathcal D}(\alpha,\beta)\)为对偶问题的最优值。

\(d^*,b^*\)有如下关系：

\[d^*\leq p^* \]

但在一些特殊条件下，\(d^*= p^*\)，此时可以通过求解对偶优化问题来得到原始优化问题的解。下面介绍这些条件：

KKT(Karush-Kuhn-Tucker)条件

假设：优化目标函数\(f\)、不等式约束函数\(g_i\)是凸函数，\(h_i(w)=a_i^Tw+b_i\)(对\(w\)向量中各元素的线性组合加上偏置)；一定存在一个w，使得对于任意的\(g_i(w)\)，满足\(g_i(w)<0\)

在有了这些假设的前提下，一定存在\(w^*,\alpha^*,\beta^*\)，\(w^*\)是原始优化问题的最优解，\(\alpha^*,\beta^*\)是对偶优化问题的最优解。\(w^*,\alpha^*,\beta^*\)，\(w^*\)满足KKT条件：

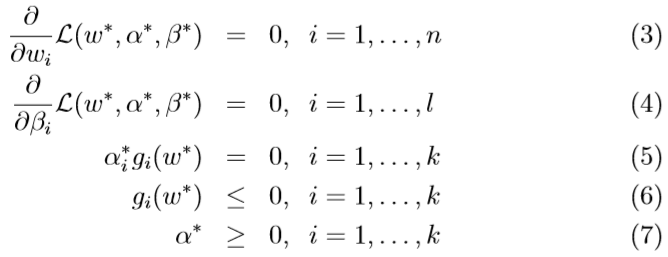
其中，等式(5)被称为KKT对偶互补条件(KKT dual complementarity condition)，\(\alpha_i^*>0\)时等式(5)表明\(g_i(w^*)=0\)，之后会提到，(5)的这一性质表明只有少量的训练样本充当支持向量

SVM目标函数的最优化

首先回顾SVM的原始优化目标：

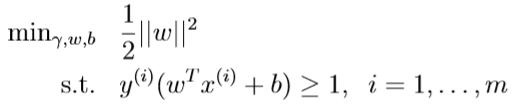
不等式约束条件可以写为：

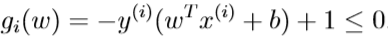
若\(g_i(w)\)的拉格朗日乘子\(\alpha_i^*>0\)，则由KKT条件的等式(5)可得\(g_i(w)=0\)，样本i是最靠近决策边界的点,其几何边界(函数边界)值最小(因为不可能有其他点使得\(y^{(i)}(w^Tx^{(i)}+b)<1\)),这样的样本i被称为支持向量

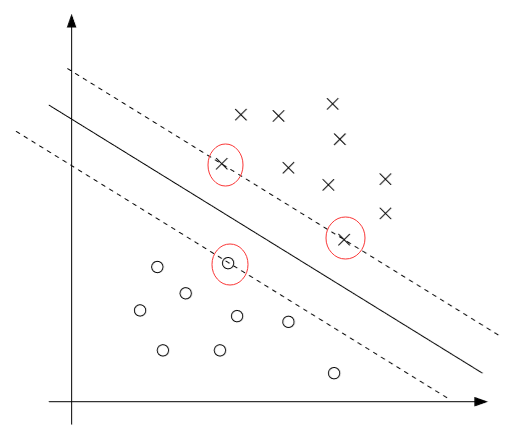
如上图所示，红圈圈出的三个样本到决策边界的函数边界(几何边界)为1，是支持向量，从图中可见，支持向量的个数一般小于训练样本的个数

下面构造广义拉格朗日函数：

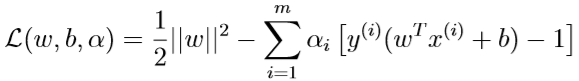
\(w,b\)是要求出最优解的参数，\(\alpha_i\)是拉格朗日乘子。

原始优化问题的对偶问题为：

\[\max_{\alpha:\alpha\geq 0}\theta_{\mathcal D}(\alpha)=\max_{\alpha:\alpha\geq 0}\min_{w,b}\mathcal L(w,b,\alpha) \]

首先在已知\(\alpha\)的前提下求\(\theta_{\mathcal D}(\alpha)\)，这就需要求出\(\arg \min_{w,b}\mathcal L(w,b,\alpha)\).令关于\(w,b\)的函数\(\mathcal L\)对\(w,b\)偏导数分别为0：

\[\frac{\partial \mathcal L(w,b,\alpha)}{\partial b}=-\sum_{i=1}^m\alpha_iy^{(i)}=0 \]

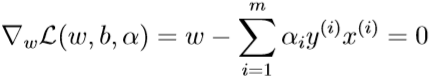
解得：

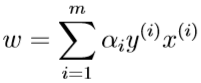
代入\(\mathcal L(w,b,\alpha)\)，得到\(\min_{w,b}\mathcal L(w,b,\alpha)\)的表达式：

\[\min_{w,b}\mathcal L(w,b,\alpha)=\sum_{i=1}^m\alpha_i+\frac 1 2 w^Tw-\sum_{i=1}^m\alpha_i[y^{(i)}((\sum_{j=1}^m(\alpha_jy^{(j)}x^{(j)})^T)x^{(i)}+b)] \]

\[=\sum_{i=1}^m\alpha_i+\frac 1 2 (\sum_{i=1}^m\alpha_iy^{(i)}(x^{(i)})^T)(\sum_{j=1}^m\alpha_jy^{(j)}x^{(j)})-\sum_{i=1}^m\alpha_i[y^{(i)}((\sum_{j=1}^m\alpha_jy^{(j)}(x^{(j)})^Tx^{(i)})+b)] \]

\[=\sum_{i=1}^m\alpha_i+\frac 1 2 \sum_{i=1}^m\sum_{j=1}^m(\alpha_i\alpha_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)})-\sum_{i=1}^m\alpha_i[y^{(i)}(\sum_{j=1}^m\alpha_jy^{(j)}(x^{(i)})^Tx^{(j)})]-b\sum_{i=1}^m\alpha_i y^{(i)} \]

\[=\sum_{i=1}^m\alpha_i+\frac 1 2 \sum_{i=1}^m\sum_{j=1}^m(\alpha_i\alpha_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)})-\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)}-b\sum_{i=1}^m\alpha_i y^{(i)} \]

\[=\sum_{i=1}^m\alpha_i-\frac 1 2 \sum_{i=1}^m\sum_{j=1}^m(\alpha_i\alpha_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)})-b\sum_{i=1}^m\alpha_i y^{(i)} \]

(两个列向量x,y，\(x^Ty=y^Tx\))

其中，\(\sum_{i=1}^m\alpha_iy^{(i)}=0\)，则

\[\mathcal L(w,b,\alpha)=\sum_{i=1}^m\alpha_i-\frac 1 2 \sum_{i=1}^m\sum_{j=1}^m(\alpha_i\alpha_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)}) \]

所以对偶优化问题可以表示为

\[\max_\alpha \min_{w,b}\mathcal L(w,b,\alpha)=\max_\alpha [\sum_{i=1}^m\alpha_i-\frac 1 2 \sum_{i=1}^m\sum_{j=1}^m(\alpha_i\alpha_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)})] \]

\[=\max_\alpha [\sum_{i=1}^m\alpha_i-\frac 1 2 \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy^{(i)}y^{(j)}(x^{(i)}\cdot x^{(j)})] \]

\[\mathrm{s.t.}\ \ \alpha_i\geq 0,i=1,\cdots,m \]

\[\sum_{i=1}^m \alpha_i y^{(i)}=0 \]

(这里将列向量的转置与列向量之积表示成内积形式，方便后面使用核技巧)

该对偶优化问题满足KKT条件，因此求得的最优解\(\alpha^*\)对应于原始优化问题的最优解\(w^*,b^*\)

如果现在已经求出了\(\alpha^*\)，将其代入：

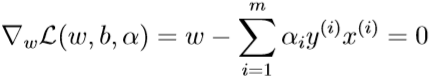
可得\(w^*\)，再考虑求出\(b^*\)的最优解，回顾之前的图：

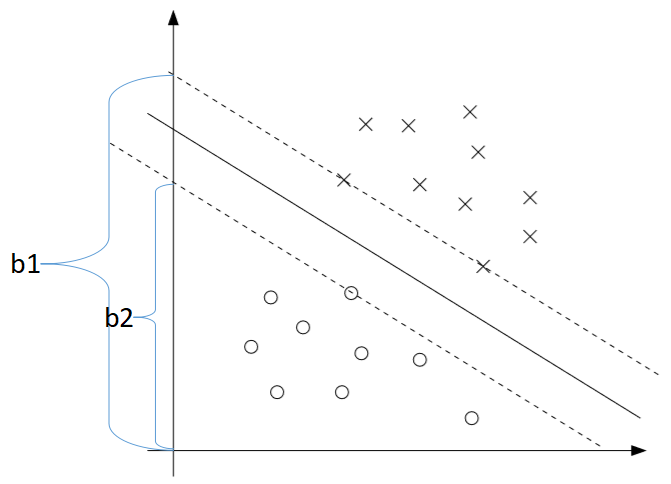
对应于正样本(X)的截距

\[b_1=\min_{i:y^{(i)}=1}(1-w^{*T}x^{(i)}) \]

对应于负样本(O)的截距

\[b_2=\max_{i:y^{(i)}=-1}(-1-w^{*T}x^{(i)}) \]

最优的截距\(b^*\)应取二者的平均值：

\[b^*=\frac 1 2 (b_1+b_2)=-\frac {\min_{i:y^{(i)}=1}w^{*T}x^{(i)}+\max_{i:y^{(i)}=-1}w^{*T}x^{(i)}}{2} \]

在预测输入样本\(x\)的分类时，若\(w^Tx+b\geq 0\)则输出1，否则输出-1，改写\(w^Tx+b\)：

\[w^Tx+b=(\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)})^Tx+b \]

\[=[\sum_{i=1}^m\alpha_iy^{(i)}(x^{(i)})^Tx]+b \]

\[=[\sum_{i=1}^m\alpha_iy^{(i)}(x^{(i)}\cdot x)]+b \]

(这里将列向量的转置与列向量之积表示成内积形式，方便后面使用核技巧)

核技巧

上面介绍的SVM只能适用于线性可分的问题，为了解决线性不可分问题，这样的SVM必须人工提取一些高阶特征。

定义原始的输入值为输入属性(input attributes)，从原始输入值人工构造、提取得到的是输入特征(input features)，输入属性到输入特征的映射\(\phi\)为特征映射(feature mapping)。

例如，原始输入只有一个标量x，人工构造出这样的特征\(x,x^2,x^3\)，则映射$$\phi(x)=(x,x^2,x3)^T$$

对于一个映射\(\phi(x)\)，定义其对应的核函数:

\[K(x,z)=\phi(x)^T\phi(z) \]

其中，x和z是原始的输入属性

如果要用人工构造的高阶特征代替原始的输入属性，只需要确定映射\(\phi\)，并用\(K(x,z)\)代替之前那几个公式里的向量内积即可。

如果已知\(\phi\)，则可以很容易地计算出\(K(x,z)\)，但一般映射得到的输入特征往往维度很高，\(\phi(x)\)很难确定也很难计算，这里可以考虑,跳过求\(\phi(x)\)的过程，直接求解\(K(x,z)\)

例如，若\(x,z\in \mathbb{R}^3,K(x,z)=(x^Tz)^2\)，映射函数可以表示为

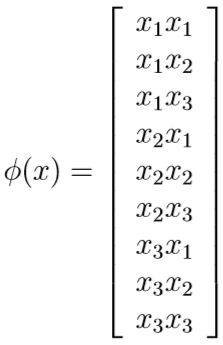
先计算\(\phi(x),\phi(z)\)再计算\(K(x,z)\)，时间复杂度为\(O(n^2)\)，但直接计算\(K(x,z)\)，时间复杂度为\(O(n)\)

如果\(\phi(x),\phi(z)\)很相似，那么\(K(x,z)=\phi(x)^T\phi(z)\)会很大，而二者如果差异很大(接近正交)，则\(K(x,z)\)会很小。所以\(K(x,z)\)可以表示对\(\phi(x),\phi(z)\)(或者说x,z)相似性的度量。

常见的核函数有高斯核(Gaussian kernel)

\[K(x,z)=\exp(-\frac{\|x-z\|^2}{2\sigma^2}) \]

判断核函数K是否是有效的核函数的方法：对于任意的m个向量\(\{x^{(1)},\cdots,x^{(m)}\}\)，对应的核矩阵(kernel matrix)为K，\(K_{i,j}=K(x^{(i)},x^{(j)})\),若K为半正定矩阵，则K是有效的核函数

讨论：正则化与不可分(non-separable)的情况

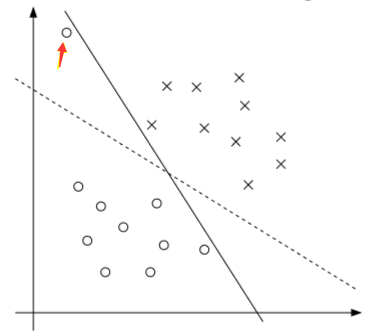
实际场景中，训练集中正负样本之间一般是不可能完美分割开的，即使能完美分割开，由于少量训练样本的干扰，会导致间隔太小，如上图

为了解决这种问题，就要给SVM的优化目标引入正则化

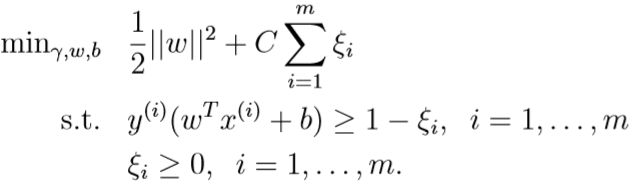
C是惩罚系数。如果\(y^{(i)}(w^Tx^{(i)}+b)\)比1小\(\xi_i\)，要付出额外代价\(C\xi_i\)，若是大于等于1，则不需要额外付出代价，这就允许一些样本不满足原来的约束条件，不满足的程度越大，付出的额外代价越大

重新构造广义拉格朗日函数：

其中,\(\alpha_i,\xi_i\)为不等式约束条件的拉格朗日乘子

类似之前不加正则化时的方法，将原始优化问题转化为对偶优化问题：

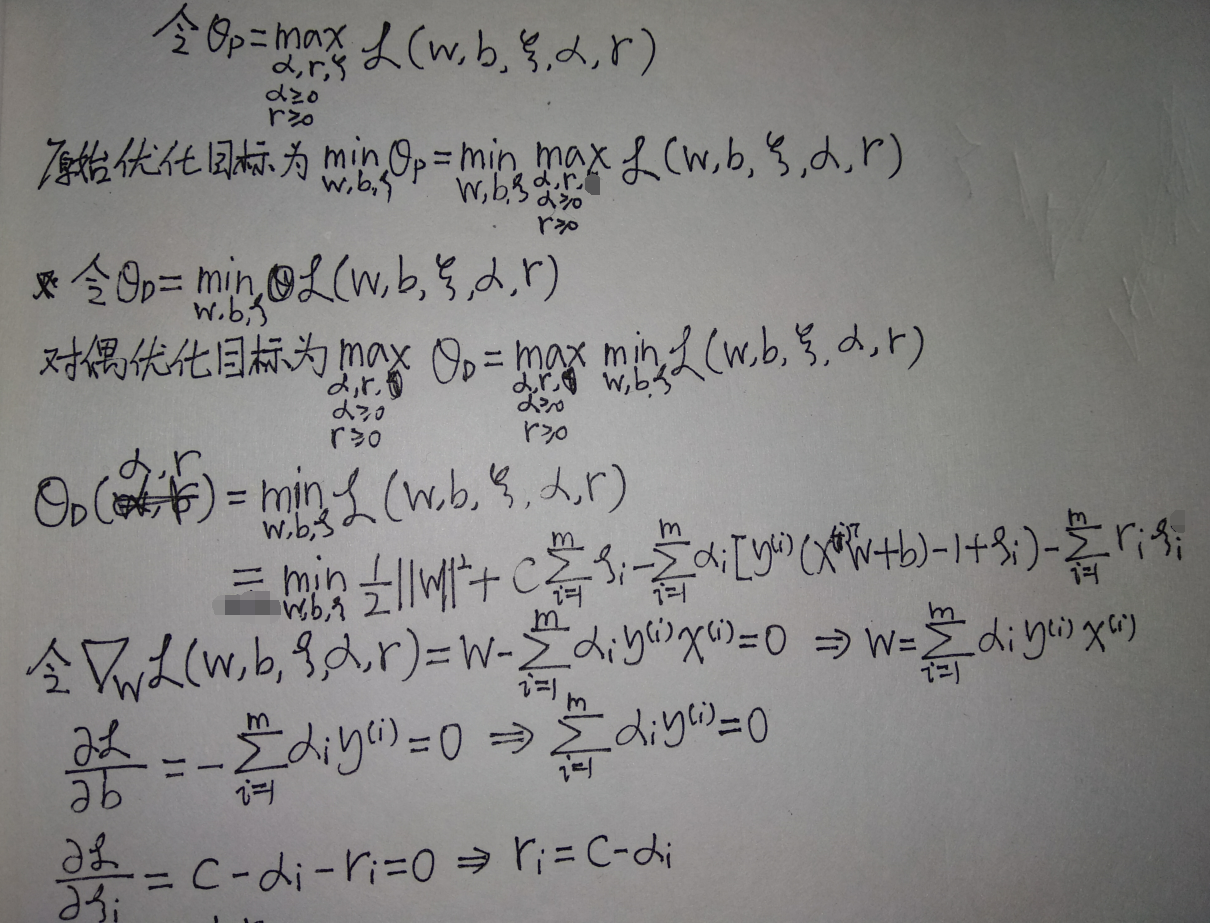
最终的优化目标消去了\(r_i\)，只与\(\alpha\)有关

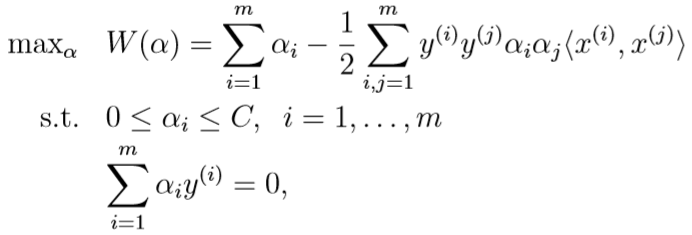
类似不加正则化时的情况，求出该优化问题的最优解\(\alpha^*\)后，就能根据\(w=\sum_{i=1}^m \alpha_i y^{(i)}x^{(i)}\)得到\(w^*\)，然后用\(b^*=\frac 1 2 (b_1+b_2)\)求出\(b^*\)

坐标上升算法、SMO优化算法

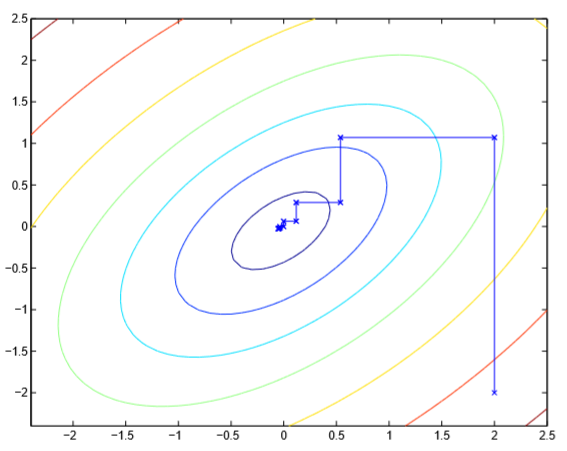
坐标上升算法

考虑最大化无约束条件的函数\(W(\alpha_1,\cdots,\alpha_m)\)，坐标上升算法就是，每次迭代，对m个参数分别更新一次，其中，更新第i个参数时，其他m-1个参数的值保持不变，伪代码如下：

参数取值的更新过程如下：

SMO(Sequential Minimal Optimization)优化算法

对于带正则化的SVM的对偶优化问题

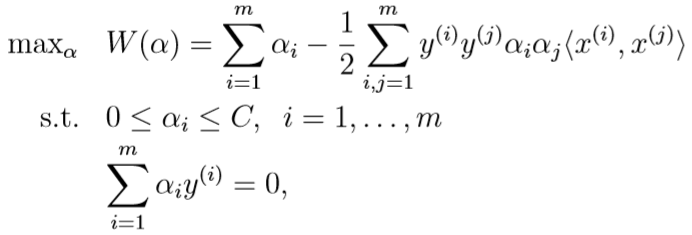
如果采用上面的坐标上升算法，每次只改变一个\(\alpha_i\)的取值，是不可行的，因为其第二个约束条件决定了：

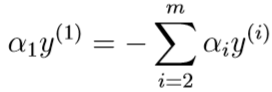
因为\(y^{(i)}\in\{0,1\},(y^{(i)})^2=1\),所以左右同乘\(y^{(1)}\)可得

等式右边是常数，所以只改变一个\(\alpha_1\)是不可行的，只能同时改变两个参数\(\alpha_i,\alpha_j\)的取值。若现在要同时改变两个参数\(\alpha_1,\alpha_2\)，由第二个约束条件可得

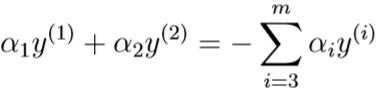
等式右边是常数，可以用\(\zeta\)替代：

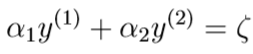
这一线性方程在坐标系中如下图所示，其中红色部分是\((\alpha_1,\alpha_2)\)的合法解构成的线段

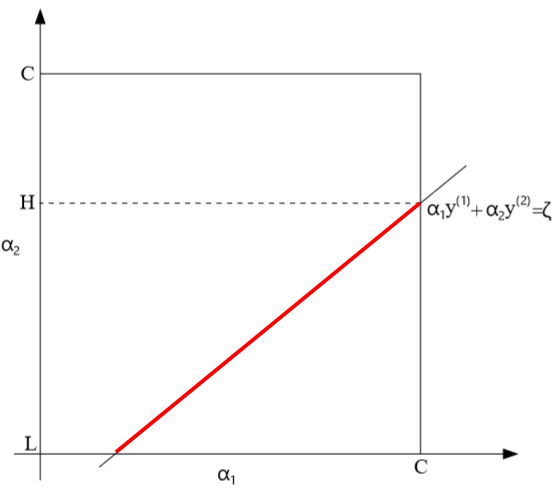
其中，\(0\leq \alpha_1,\alpha_2\leq C\)，这个约束条件在图中是一个矩形区域，决定了\(\alpha_2\)的合法取值区间为\([L,H]\subset [0,C]\)

然后我们把\(\alpha_1\)看作是关于\(\alpha_2\)的函数，\(W(\alpha)\)可以表示为关于\(\alpha_2\)的二次函数\(a\alpha_2^2+b\alpha_2+c\)，当\(\alpha_2\in[L,H]\)时，\(\alpha\)满足对偶优化问题的约束条件。对偶问题的优化目标变为

\[\max_{\alpha_2\in[L,H]} a\alpha_2^2+b\alpha_2+c \]

设\(a_2^{new,unclipped}=\arg \max_{\alpha_2} (a\alpha_2^2+b\alpha_2+c)\)(无约束条件下该二次函数的最优解)，则

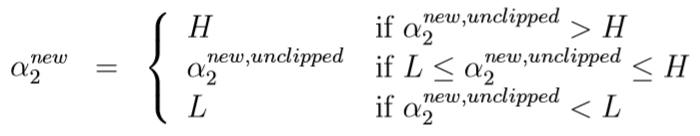
最终SMO算法可以用下面的伪代码描述：