广义线性模型(Generalized Linear Models,GLM)
指数分布族(Exponential Family Distributions)
指数分布族被定义为:
\[p(y;\eta)=b(y)\exp(\eta^TT(y)-a(\eta))
\]
其中\(\eta\)是自然参数(natural parameter);\(T(y)\)是充分统计量(sufficient statistic),一般\(T(y)=y\);\(a(\eta)\)是对数分割函数(log partition function),\(e^{-a(\eta)}\)起着归一化常数(normalization constant)的作用,保证了\(p(y;\eta)\)的积分值为1
伯努利分布、高斯分布都属于指数分布族
伯努利分布与指数分布族
对于伯努利分布:
\[p(y;\phi)=\phi^y(1-\phi)^{1-y}
\]
\[=\phi^y(1-\phi)^{1-y}
\]
\[=\exp(\log(\phi^y(1-\phi)^{1-y}))
\]
\[=\exp(y\log \phi+(1-y)\log(1-\phi))
\]
\[=\exp((\log (\frac \phi {1-\phi}))y+\log(1-\phi))
\]
此时,标量\(\eta=\log (\frac \phi {1-\phi})\),则\(\phi=\frac {e^\eta}{1+e^\eta}\);取
\[b(y)=1
\]
\[T(y)=y
\]
\[a(\eta)=-\log(1-\phi)=-\log(1-\frac {e^\eta}{1+e^\eta})=\log(1+e^\eta)
\]
这表明伯努利分布可以通过指数分布表示
高斯分布与指数分布族
由于\(\sigma^2\)对最终选取的最优的\(\theta\)没有影响,因此这里将其视为常数,不妨取\(\sigma^2=1\)
\[p(y;\mu)=\frac 1 {\sqrt{2\pi}}\exp(-\frac 1 2 (y-\mu)^2)
\]
\[=\frac 1 {\sqrt{2\pi}}\exp(-\frac 1 2 y^2)\exp(\mu y-\frac 1 2 \mu^2)
\]
取
\[b(y)=\frac 1 {\sqrt{2\pi}}\exp(-\frac 1 2 y^2)
\]
\[\eta=\mu
\]
\[T(y)=y
\]
\[a(\eta)=\frac 1 2 \mu^2=\frac 1 2 \eta^2
\]
可见高斯分布也可以通过指数分布表示
构建广义线性模型
任何GLM模型都遵循以下三条假设:
-
- \(y|x;\theta \sim\)指数分布族\((\eta)\),即,给出\(x\),参数\(\theta\),真实输出\(y\)服从某种参数为\(\eta\)的指数分布
-
- 给定\(x\),目的是预测真实输出\(T(y)\),一般情况下\(T(y)=y\),这意味着要求选取恰当的\(\theta\)使得\(h_\theta(x)\)的输出满足\(h_\theta(x)=E[y|x]\)(其中\(E[y|x]\)是给定输入\(x\),输出值的期望),例如在逻辑回归中应有:
\[h_\theta(x)=0\cdot p(y=0|x;\theta)+1\cdot p(y=1|x;\theta)=E[y|x]
\]
-
- 指数分布的参数\(\eta=\theta^Tx\),若\(\eta\)是向量,则\(\eta_i=\theta_i^Tx\),这个假设体现出这个模型是线性的。
从GLM看最小二乘法的假设函数
在最小二乘法中,由变量x决定的目标变量(响应变量)y是连续的,服从高斯分布\(\mathcal{N}(\mu,\sigma^2)\)(\(\mu\)可能是由\(x\)决定的参数),则最小二乘法的假设函数\(h_\theta(x)\)为:
\[h_\theta(x)=E[y|x;\theta]
\]
(假设2)
\[=\mu
\]
(y服从高斯分布,\(\mathcal{N}(\mu,\sigma^2)\),其期望为\(\mu\))
\[=\eta
\]
(在"高斯分布与指数分布族"一节中已推出\(\mu=\eta\))
\[=\theta^Tx
\]
(假设3)
从GLM看逻辑回归的假设函数
在二分类逻辑回归中,目标变量\(y\in\{0,1\}\),服从伯努利分布,\(y|x;\theta\sim \mathrm{Bernoulli(\phi)}\),之前在"伯努利分布与指数分布族"一节中已得出\(\phi=\frac {e^\eta}{1+e^\eta}=\frac {1}{1+e^{-\eta}}\),从而:
\[h_\theta(x)=E[y|x;\theta]
\]
(假设2)
\[=\phi
\]
(\(y|x;\theta\sim\mathrm{Bernoulli(\phi)}\)的期望为\(\phi\))
\[=\frac {1}{1+e^{-\eta}}
\]
\[=\frac {1}{1+e^{-\theta^Tx}}
\]
(假设3)
GLM与Softmax回归
Softmax回归的假设函数
考虑多元分类问题:数据的真实标签\(y\in\{1,2,\cdots,k\}\),不采用多元逻辑回归,直接一次性得到分类结果。
我们用多项式分布(multinomial distribution)建模,该分布由参数\(\phi_1,\cdots,\phi_{k-1}\)决定,为方便描述,令\(\phi_k=1-\sum_{i=1}^{k-1}\phi_i\),注意,它不是参数,参数只有k-1个
另外,\(T(y)\in \mathbb{R}^{k-1}\)
\[T(1)=(1,0,\cdots,0)^T
\]
\[T(2)=(0,1,0,\cdots,0)^T
\]
\[T(k-1)=(0,\cdots,0,1)^T
\]
\[T(k)=(0,\cdots,0)^T
\]
记符号\(1\{True\}=1,1\{False\}=0\),则
\[T(y)_i=1\{y=i\}
\]
从而
\[E[T(y)_i]=P(y=i)=\phi_i
\]
目标变量y的概率分布为:
\[p(y;\phi)=\phi_1^{1\{y=1\}}\cdots\phi_k^{1\{y=k\}}
\]
\[=\phi_1^{1\{y=1\}}\cdots\phi_{k-1}^{1\{y=k-1\}}\phi_k^{1-\sum_{i=1}^{k-1}1\{y=i\}}
\]
\[=\phi_1^{(T(y))_1}\cdots\phi_{k-1}^{(T(y))_{k-1}}\phi_k^{1-\sum_{i=1}^{k-1}{(T(y))_i}}
\]
\[=\exp((T(y))_1\log\phi_1\cdots{(T(y))_{k-1}}\log\phi_{k-1}+(1-\sum_{i=1}^{k-1}{(T(y))_i})\log \phi_k)
\]
\[=\exp((T(y))_1\log{\frac {\phi_1}{\phi_k}}\cdots{(T(y))_{k-1}}\log{\frac {\phi_{k-1}}{\phi_k}}+\log \phi_k)
\]
\[=b(y)\exp(\eta^TT(y)-a(\eta))
\]
其中,
\[\eta=\begin{pmatrix}
\log{\frac {\phi_1}{\phi_k}}\\
\vdots\\
\log{\frac {\phi_{k-1}}{\phi_k}}
\end{pmatrix}\]
\[a(\eta)=-\log\phi_k
\]
\[b(y)=1
\]
可见多项式分布可以用指数分布表示,其中
\[\eta_i=\log{\frac{\phi_i}{\phi_k}}
\]
\[e^{\eta_i}=\frac{\phi_i}{\phi_k}
\]
可得:
\[\phi_k\sum_{i=1}^ke^{\eta_i}=1
\]
\[\phi_k=\frac 1 {\sum_{i=1}^ke^{\eta_i}}
\]
\[\phi_i=\frac {e^{\eta_i}} {\sum_{j=1}^ke^{\eta_j}}
\]
(这一函数从\(\eta\)映射到\(\phi\),称为Softmax函数)
根据之前的假设3,$$\eta_i=\theta_i^Tx$$
可得
\[\phi_i=\frac {e^{\theta_i^Tx}} {\sum_{j=1}^ke^{\theta_j^Tx}}
\]
\[p(y=i|x;\theta)=\phi_i=\frac {e^{\theta_i^Tx}} {\sum_{j=1}^ke^{\theta_j^Tx}}
\]
这被称为Softmax回归,其假设函数
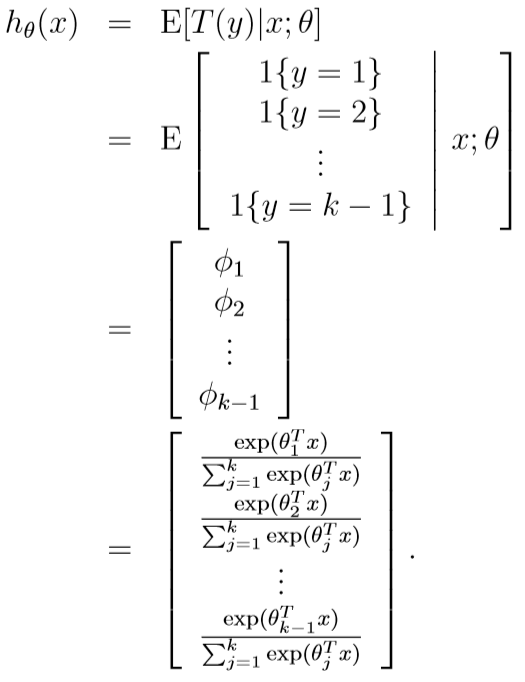
\(p(y=k|x;\theta)\)可以由\(1-\sum_{i=1}^{k-1}p(y=i|x;\theta)=1-\sum_{i=1}^{k-1}\phi_i\)求得
Softmax回归的误差函数
Softmax回归的误差函数也可以通过最大化似然估计得到。
似然估计函数:
\[L(\theta)=\prod_{i=1}^m p(y^{(i)}|x^{(i)};\theta)
\]
对数似然
\[l(\theta)=\sum_{i=1}^m \log(p(y^{(i)}|x^{(i)};\theta))
\]
\[=\sum_{i=1}^m \log(\prod_{l=1}^k (p(y^{(i)}=l|x^{(i)};\theta))^{1\{y^{(i)}=l\}})
\]
\[=\sum_{i=1}^m \log(\prod_{l=1}^k (\frac {e^{\theta_l^Tx^{(i)}}} {\sum_{j=1}^ke^{\theta_j^Tx^{(i)}}})^{1\{y^{(i)}=l\}})
\]
优化目标就是
\[\arg \max_\theta l(\theta)
\]
高斯判别分析模型(Gaussian Discriminant Analysis Model,GDA)
假设现在有一个二分类问题,输入特征向量\(x\)的每个元素都是连续值,则我们可以将样本标签y的分布(evidence)视为参数为\(\phi\)的伯努利分布:
\[y\sim \mathrm{Bernoulli}(\phi)
\]
将\(p(x|y)\)(样本标签为0(1)时,输入特征的分布)视为多元高斯分布:
\[x|y=0\sim \mathcal N (\mu_0,\Sigma)
\]
\[x|y=1\sim \mathcal N (\mu_1,\Sigma)
\]
写出公式:
\[p(y)=\phi^y(1-\phi)^{1-y}
\]
\[p(x|y=0)=\frac 1 {(2\pi)^{\frac n 2}|\Sigma|^{\frac 1 2}}\exp (-\frac 1 2(x-\mu_0)^T\Sigma^{-1}(x-\mu_0))
\]
\[p(x|y=1)=\frac 1 {(2\pi)^{\frac n 2}|\Sigma|^{\frac 1 2}}\exp (-\frac 1 2(x-\mu_1)^T\Sigma^{-1}(x-\mu_1))
\]
注意:这里的多元高斯分布模型,y=0和y=1时的均值\(\mu_0,\mu_1\)不同,但协方差矩阵是完全一样的
由参数\(\phi,\mu_0,\mu_1,\Sigma\)决定的对数似然
\[l(\phi,\mu_0,\mu_1,\Sigma)=\log \prod_{i=1}^m p(x^{(i)},y^{(i)};\phi,\mu_0,\mu_1,\Sigma)
\]
\[=\log \prod_{i=1}^m p(x^{(i)}|y^{(i)};\phi,\mu_0,\mu_1,\Sigma)p(y^{(i)};\phi)
\]
通过最大化对数似然函数可得,
\[\phi=\frac 1 m \sum_{i=1}^m1\{y^{(i)}=1\}
\]
\[\mu_0=\frac {\sum_{i=1}^m 1\{y^{(i)}=0\}x^{(i)}}{\sum_{i=1}^m 1\{y^{(i)}=0\}}
\]
\[\mu_1=\frac {\sum_{i=1}^m 1\{y^{(i)}=1\}x^{(i)}}{\sum_{i=1}^m 1\{y^{(i)}=1\}}
\]
\[\Sigma=\frac 1 m \sum_{i=1}^m (x^{(i)}-\mu_{y^{(i)}})(x^{(i)}-\mu_{y^{(i)}})^T
\]
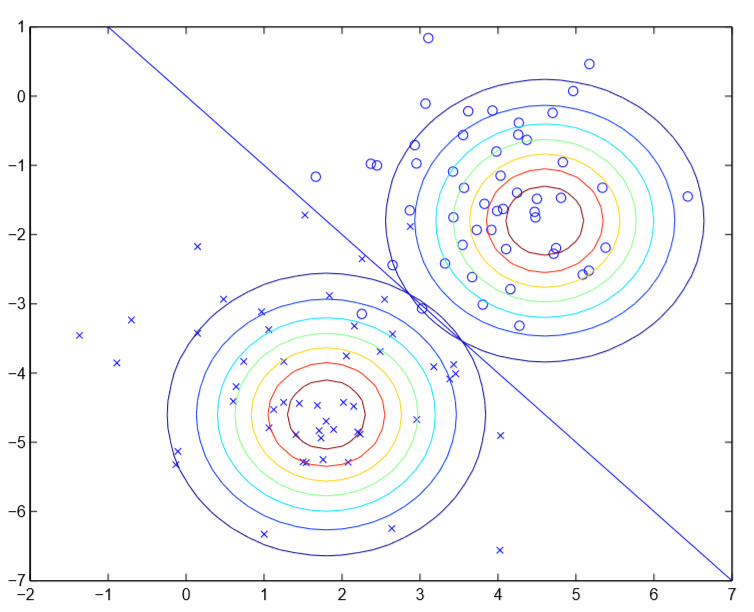
可见图中y=0和1的高斯分布等高线图,除了中心不同以外,其他完全相同。在\(p(y=1|x)>p(y=0|x)\)时,模型输出分类为1,反之为0,使得\(p(y=1|x)=p(y=0|x)=0.5\)的点\(x\)在图中可以构成一条直线(决策边界)
GDA vs. 逻辑回归
若我们将\(p(y=1|x;\phi,\mu_0,\mu_1,\Sigma)\)视为一个关于n+1维列向量x的函数,则
\[p(y=1|x;\phi,\mu_0,\mu_1,\Sigma)=\frac 1 {1+\exp(-\theta^Tx)}
\]
其中\(\theta\)是关于\(\phi,\mu_0,\mu_1,\Sigma\)的函数,上式与逻辑回归的假设函数\(h_\theta(x)=p(y=1|x;\theta)\)是完全一样的
从上面的图可以看出,如果假设\(p(x|y)\)服从多元高斯分布,则可以推出假设\(p(y|x)\)是逻辑回归的假设函数形式;但是如果假设\(p(y|x)\)是逻辑回归的假设函数形式,显然无法推出假设\(p(x|y)\)服从多元高斯分布,决策边界两侧的正负样本分布可以随意,不一定要近似多元高斯分布。
这表明GDA的假设比逻辑回归的假设更强,GDA不仅假设决策边界是线性的,而且假设正样本、负样本服从多元高斯分布,逻辑回归只假设决策边界是线性的
但当正负样本的分布的确满足GDA的假设时,GDA比逻辑回归表现得更高效(asymptotically efficient),即,在训练样本数目很少时,GDA的准确率更高。
反之,由于逻辑回归的假设更弱,因此逻辑回归表现得更鲁棒、受输入数据的分布特性的影响更小,在对非高斯分布(non-Gaussian)的数据时表现更好,因此一般来讲,逻辑回归比GDA用得更多
朴素贝叶斯(Naive Bayes)
GDA中,特征向量x中每个元素都是连续值,现在考虑一种不同的学习算法,其特征向量x中每个元素都是离散值
在垃圾邮件过滤问题中,输入特征向量\(x\)中\(x_i=1\)表示词库中第i个词出现过,反之没有出现过,现在要通过特征向量\(x\)预测邮件是否是垃圾邮件(\(y=0/1\))
现在对\(p(x|y)\)建模,在这个问题中,特征向量\(x\)的维度一般很大(50000),如果采用多项式分布的话,则给定x,得到的结果有\(2^{50000}\)种,则参数向量就是\(2^{50000}-1\)维的,显然不可行。
朴素贝叶斯算法对\(p(x|y)\)作出了一个很强的假设:由\(y\)决定的\(x\),其中任意两个元素\(x_i,x_j\)的取值是相互条件独立(conditionally independent)的,即,若已知\(p(x_i|y)\),则其不会影响\(p(x_j|y)\)的取值。则\(p(x_j|y)=p(x_j|y,x_i)\)(给定\(y\),得到的\(x_j\)的概率,与给定\(y,x_i\),得到的\(x_j\)的概率,完全相同)
\[p(x_1,\cdots,x_n |y)=p(x_1|y)p(x_2|y,x_1)\cdots p(x_n|y,x_1,\cdots,x_{n-1})
\]
(根据概率的性质)
\[=\prod_{i=1}^n p(x_i|y)
\]
(朴素贝叶斯假设)
模型参数
\[\phi_{i|y=1}=p(x_i=1|y=1)
\]
\[\phi_{i|y=0}=p(x_i=1|y=0)
\]
\[\phi_{y}=p(y=1)
\]
极大似然估计
给定训练集\(\{(x^{(i)},y^{(i)})|i=1,\cdots,m\}\),则其似然估计为
\[\mathcal L(\phi_y,\phi_{i|y=0},\phi_{i|y=1})=\prod_{i=1}^m p(x^{(i)},y^{(i)})
\]
最大化该函数,得到参数取值为:
\[\phi_{j|y=1}=\frac {\sum_{i=1}^m1\{x_j^{(i)}=1 \wedge y^{(i)}=1\}}{\sum_{i=1}^m1\{y^{(i)}=1\}}
\]
(标签为1的所有训练样本中,\(x_j^{(i)}=1\)的比例)
\[\phi_{j|y=0}=\frac {\sum_{i=1}^m1\{x_j^{(i)}=1 \wedge y^{(i)}=0\}}{\sum_{i=1}^m1\{y^{(i)}=0\}}
\]
(标签为0的所有训练样本中,\(x_j^{(i)}=1\)的比例)
\[\phi_{y}=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}} {m}
\]
(标签为1的训练样本的比例)
假设函数
\[p(y=1|x)=\frac {p(x|y=1)p(y=1)}{p(x)}
\]
\[=\frac {(\prod_{i=1}^np(x_i|y=1))p(y=1)}{p(x|y=1)p(y=1)+p(x|y=0)p(y=0)}
\]
\[=\frac {(\prod_{i=1}^np(x_i|y=1))p(y=1)}{(\prod_{i=1}^np(x_i|y=1))p(y=1)+(\prod_{i=1}^np(x_i|y=0))p(y=0)}
\]
其中,\(x_i=1\)时\(p(x_i|y=1)=\phi_{i|y=1}\),\(p(x_i|y=0)=\phi_{i|y=0}\);\(x_i=0\)时\(p(x_i|y=1)=1-\phi_{i|y=1}\),\(p(x_i|y=0)=1-\phi_{i|y=0}\)
若\(p(y=1|x)>p(y=0|x)\),输出分类为1,反之输出分类为0
拉普拉斯平滑(Laplace Smoothing)
设词库里第n个词为"NIPS",该词在之前的所有训练样本中都没有出现过,则根据之前的公式,有:
\[\phi_{n|y=1}=\frac {\sum_{i=1}^m1\{x_n^{(i)}=1 \wedge y^{(i)}=1\}}{\sum_{i=1}^m1\{y^{(i)}=1\}}=0
\]
\[\phi_{n|y=0}=\frac {\sum_{i=1}^m1\{x_n^{(i)}=1 \wedge y^{(i)}=0\}}{\sum_{i=1}^m1\{y^{(i)}=0\}}=0
\]
\[p(y=1|x)=\frac {(\prod_{i=1}^np(x_i|y=1))p(y=1)}{(\prod_{i=1}^np(x_i|y=1))p(y=1)+(\prod_{i=1}^np(x_i|y=0))p(y=0)}=\frac 0 0
\]
这个式子是没有意义的,这就无法对输入样本做出预测了
回顾多项式分布,若随机变量\(z\in \{1,2,\cdots,k\}\)服从多项式分布,则多项式分布的参数\(\phi_i=p(z=i)\);给出m个z的观测值\(\{z^{(1)},\cdots,z^{(m)}\}\),极大似然估计后,参数
\[\phi_j=\frac {\sum_{i=1}^m1\{z^{(i)}=j\}} m
\]
(m个观测值中取值为j的比例)
若随机变量z的某些取值j在观测样本中从未出现过,这些\(\phi_j=0\),而拉普拉斯平滑修改了一下上式,解决了这个问题:
\[\phi_j=\frac {\sum_{i=1}^m1\{z^{(i)}=j\}+1} {m+k}
\]
此时仍有\(\sum_{j=1}^k\phi_j=1\),但是即使某个取值j在观测样本中从未出现过,\(\phi_j=\frac 1 {m+k}\neq 0\)
回到朴素贝叶斯算法中:
\[\phi_{j|y=1}=\frac {\sum_{i=1}^m1\{x_j^{(i)}=1 \wedge y^{(i)}=1\}+1}{\sum_{i=1}^m1\{y^{(i)}=1\}+2}
\]
\[\phi_{j|y=0}=\frac {\sum_{i=1}^m1\{x_j^{(i)}=1 \wedge y^{(i)}=0\}+1}{\sum_{i=1}^m1\{y^{(i)}=0\}+2}
\]
\[\phi_{y}=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}} {m}
\]
(一般正样本是存在的,\(\phi_y\)大于0,不必对其公式作修改)
事件模型(Event Model)实现垃圾邮件过滤
在垃圾邮件过滤问题中,之前提到的朴素贝叶斯算法使用的是多元伯努利事件模型(multi-variate Bernoulli event model),这个模型有如下假设:
下面介绍一种新的模型:多项式事件模型,首先约定一些符号:
\(x_i\)表示邮件中第i个单词,\(x_i\in\{1,\cdots,|V|\}\),\(|V|\)是词库的大小,于是一封由n个单词组成的邮件可以用n维向量\((x_1,\cdots,x_n)\)表示(注意,不同的邮件的n可能不同),比如词库里第一个单词为A,第35000个单词为NIPS,则"A NIPS"可以用向量\(\{1,35000\}^T\)表示。
在多项式事件模型中,有如下假设:
模型参数
\[\phi_y=p(y)
\]
对于邮件中第j个单词\(x_j\),有
\[\phi_{i|y=1}=p(x_j=i|y=1)
\]
\[\phi_{i|y=0}=p(x_j=i|y=0)
\]
注意这两个参数与j无关,即最终随机选择的\(x_j\)是与其在邮件中的位置j无关的,即对于任意的j,概率分布\(p(x_j|y)\)是完全相同的
现在给出训练集\(\{(x^{(i)},y^{(i)});i=1,\cdots,m\}\),其中\(x^{(i)}=(x_1^{(i)},\cdots,x_{n_i}^{(i)})\),\(n_i\)是第i个训练样本的单词个数
则模型对训练集的似然性为:
\[\mathcal L(\phi,\phi_{i|y=0},\phi_{i|y=1})=\prod_{i=1}^m p(x^{(i)},y^{(i)})
\]
\[=\prod_{i=1}^m p(x^{(i)}|y^{(i)})p(y^{(i)})
\]
\[=\prod_{i=1}^m (\prod_{j=1}^{n_i} p(x_j^{(i)}|y^{(i)};\phi_{i|y=0},\phi_{i|y=1})))p(y^{(i)};\phi_y)
\]
通过极大似然估计可以得到参数的取值:
\[\phi_{k|y=1}=\frac {\sum_{i=1}^m\sum_{j=1}^{n_i}1\{x_j^{(i)}=k\wedge y^{(i)}=1\}}{\sum_{i=1}^m1\{y^{(i)}=1\}n_i}
\]
(词库编号为k的单词,在所有垃圾邮件中出现过的次数,除以,所有垃圾邮件的单词总数)
\[\phi_{k|y=0}=\frac {\sum_{i=1}^m\sum_{j=1}^{n_i}1\{x_j^{(i)}=k\wedge y^{(i)}=0\}}{\sum_{i=1}^m1\{y^{(i)}=0\}n_i}
\]
(词库编号为k的单词,在所有非垃圾邮件中出现过的次数,除以,所有非垃圾邮件的单词总数)
\[\phi_y=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}}{m}
\]
(垃圾邮件在所有邮件中的比例)
设一封邮件有n个单词:\(x=\{x_1,\cdots,x_n\}\),则其为垃圾邮件的概率
\[p(y=1|x)=\frac {p(x=\{x_1,\cdots,x_n\}|y=1)p(y=1)}{p(x=\{x_1,\cdots,x_n\})}
\]
\[=\frac {(\prod_{i=1}^n\phi_{x_i|y=1})\phi_{y}}{p(x=\{x_1,\cdots,x_n\}|y=1)p(y=1)+p(x=\{x_1,\cdots,x_n\}|y=0)p(y=0)}
\]
\[=\frac {(\prod_{i=1}^n\phi_{x_i|y=1})\phi_{y}}{(\prod_{i=1}^n\phi_{x_i|y=1})\phi_y+(\prod_{i=1}^n\phi_{x_i|y=0})(1-\phi_y)}
\]
如果加入拉普拉斯平滑的话,参数变为:
\[\phi_{k|y=1}=\frac {\sum_{i=1}^m\sum_{j=1}^{n_i}1\{x_j^{(i)}=k\wedge y^{(i)}=1\}+1}{\sum_{i=1}^m1\{y^{(i)}=1\}n_i+|V|}
\]
\[\phi_{k|y=0}=\frac {\sum_{i=1}^m\sum_{j=1}^{n_i}1\{x_j^{(i)}=k\wedge y^{(i)}=0\}+1}{\sum_{i=1}^m1\{y^{(i)}=0\}n_i+|V|}
\]
\[\phi_y=\frac{\sum_{i=1}^m1\{y^{(i)}=1\}}{m}
\]



