线性回归的Normal Equations
令全体训练样本构成的矩阵为
\[X=\begin{pmatrix}(x^{(1)})^T\\\vdots\\(x^{(m)})^T\end{pmatrix}
\]
对应的真实值
\[y=\begin{pmatrix}y^{(1)}\\\vdots\\y^{(m)}\end{pmatrix}
\]
参数
\[\theta=(\theta_0,\theta_1,\cdots,\theta_n)^T
\]
则有
\[X\theta=\begin{pmatrix}(x^{(1)})^T\theta\\\vdots\\(x^{(m)})^T\theta\end{pmatrix}
=\begin{pmatrix}h_\theta(x^{(1)})\\\vdots\\h_\theta(x^{(m)})\end{pmatrix}\]
\[\frac 1 2 \|X\theta-y\|^2=\frac 1 2 (X\theta-y)^T(X\theta-y)=\frac 1 2 \sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2=J(\theta)
\]
则使得\(J(\theta)\)最小的点,一定是极小值点,此时\(\frac {\partial J(\theta)}{\partial \theta_i}=0,\ \ i=0,\cdots,n\)
矩阵求导求解参数
-
- (矩阵的迹的性质)令\(A,B,C\)为n阶方阵,则\(\mathrm{tr}(AB)=\mathrm{tr}(BA)\),\(\mathrm{tr}(ABC)=\mathrm{tr}(CAB)=\mathrm{tr}(BCA)\),以此类推
设\(A\in \mathbb{R}^{m\times n}\),\(f(A)\in \mathbb{R}\),\(f:\mathbb{R}^{m\times n}\to \mathbb{R}\),则\(f(A)\)对A的梯度为:
\[\nabla_A f(A)=
\begin {pmatrix}
\frac{\partial f}{\partial A_{1,1}}&\cdots&\frac{\partial f}{\partial A_{1,n}}\\
\vdots & \ddots & \vdots\\
\frac{\partial f}{\partial A_{m,1}}&\cdots & \frac{\partial f}{\partial A_{m,n}}
\end{pmatrix}\]
下面不加证明地给出几个公式:
-
Formula 1.$$\nabla_A\mathrm{tr}(AB)=B^T$$
-
Formula 2.$$\nabla_A\mathrm{tr}(ABATC)=CAB+CTAB^T$$
-
Formula 3.$$\nabla_{AT}f(A)=(\nabla_{A}f(A))T$$
则
\[\nabla_\theta J(\theta)=\nabla_\theta [\frac 1 2 (X\theta-y)^T(X\theta-y)]
\]
\[=\frac 1 2 \nabla_\theta [(X\theta-y)^T(X\theta-y)]
\]
\[=\frac 1 2 \nabla_\theta [(\theta^T X^T-y^T)(X\theta-y)]
\]
\[=\frac 1 2 \nabla_\theta (\theta^T X^T X\theta-\theta^T X^T y-y^TX\theta+y^Ty)
\]
(注意这里nabla算子后面的是一个实数,\(\mathrm{tr}a=a\),所以可以对整个式子直接加上tr)
\[=\frac 1 2 \nabla_\theta \mathrm{tr}(\theta^T X^T X\theta-\theta^T X^T y-y^TX\theta+y^Ty)
\]
\[=\frac 1 2 \nabla_\theta [\mathrm{tr}(\theta^T X^T X\theta)-\mathrm{tr}(\theta^T X^T y)-\mathrm{tr}(y^TX\theta)]
\]
(由于\(y^Ty\)与\(\theta\)无关,因此可以消掉)
\[=\frac 1 2 \nabla_\theta [\mathrm{tr}(\theta^T X^T X\theta)-\mathrm{tr}(\theta^T X^T y)-\mathrm{tr}(\theta y^T X)]
\]
\[=\frac 1 2 \nabla_\theta [\mathrm{tr}(\theta^T X^T X\theta)-2\mathrm{tr}(\theta y^T X)]
\]
\[=\frac 1 2 \nabla_\theta [\mathrm{tr}(\theta^T X^T X\theta)-2(\theta y^T X)]
\]
(\((\theta y^T X)\)是实数,实数a有:\(\mathrm{tr}(a)=a\))
\[=\frac 1 2 \nabla_\theta [\mathrm{tr}(\theta \theta^T X^T X)-2(\theta y^T X)]
\]
\[=\frac 1 2 \nabla_\theta [\mathrm{tr}(\theta I \theta^T X^T X)-2(\theta y^T X)]
\]
\[=\frac 1 2 [X^TX\theta+X^TX\theta-2\nabla_\theta (\theta y^T X)]
\]
(使用公式2,令\(A=\theta,B=I,C=X^TX\))
\[=X^TX\theta-\nabla_\theta (\theta y^T X)
\]
\[=X^TX\theta-X^Ty=0
\]
(使用公式1)
从而可得Normal Equations:
\[X^TX\theta=X^Ty
\]
\[\theta=(X^TX)^{-1}X^Ty
\]
局部加权线性回归
局部加强线性回归是一种非参数的学习算法,可以很好地拟合一些常规线性回归模型无法拟合的数据(常规线性回归模型需要构造复杂的高阶特征)。其
缺点是每次输入一个样本,都要重新用整个训练集训练一次模型。
若当前需要查询输入向量为\(x=(1,x_1,\cdots,x_n)\)时的预测输出,则构建一个线性回归模型:\(h_\theta=\theta^Tx\),但是,这个模型的误差函数有所变化:
\[J(\theta)=\sum_{i=1}^mw^{(i)}(y^{(i)}-\theta^Tx^{(i)})^2
\]
其中,
\[w^{(i)}=\exp(-\frac{\|x^{(i)}-x\|^2}{2\tau^2})
\]
表明训练样本点\(x^{(i)}\)与\(x\)差异性越大,\(w^{(i)}\)越小,和式中\(w^{(i)}(y^{(i)}-\theta^Tx^{(i)})^2\)这一项对\(J(\theta)\)的影响就越小
注意:\(w^{(i)}\)看似与高斯分布很像,但是并非高斯分布,因为其下限负无穷,上限正无穷的反常积分,值不一定为1
这个误差函数使得最终拟合出的\(h_\theta(x)\)在输入样本\(x\)附近时的输出值接近真实输出值。
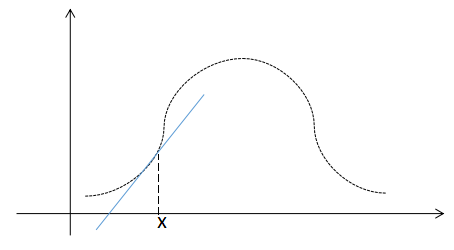
由于局部加权线性回归没有在原始特征基础上构造高阶特征,其假设函数是线性的,所以最终在给定训练样本集(图中曲线)和输入数据\(x\)时,拟合出的\(h_\theta(x)\)如图中蓝线所示,输入样本距离\(x\)越近,其预测输出与真实输出越接近
概率角度解释线性回归与逻辑回归的误差函数
概率学的极大似然估计可以解释,为什么线性回归采用均方误差函数,而逻辑回归采用交叉熵误差函数
线性回归:均方差误差函数
首先假设第i个训练数据的真实输出\(y^{(i)}\)与输入\(x\)有如下关系:
\[y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)}
\]
其中,\(\epsilon^{(i)}\)是第i个训练数据预测输出与真实输出之间的误差
假设对于所有的训练样本i,\(\epsilon^{(i)}\)之间是相互独立的(IID,independently and identically distributed)。
另外假设\(\epsilon^{(i)}\)满足高斯分布:\(\epsilon^{(i)}\sim \mathcal N (0,\sigma^2)\),换言之,其概率分布(即\(\epsilon^{(i)}\)在不同取值下的出现概率\(p\))为
\[p(\epsilon^{(i)})=\frac 1 {\sqrt{2\pi}\sigma}\exp(-\frac {(\epsilon^{(i)})^2}{2\sigma^2})
\]
也可以换一种表述方法:
\[p(y^{(i)}|x^{(i)};\theta)=\frac 1 {\sqrt{2\pi}\sigma}\exp(-\frac {(y^{(i)}-h_\theta^{(i)})^2}{2\sigma^2})
\]
\[p(y^{(i)}|x^{(i)};\theta)=\frac 1 {\sqrt{2\pi}\sigma}\exp(-\frac {(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})
\]
\(p(y^{(i)}|x^{(i)};\theta)\)表示在固定参数\(\theta\)下,受随机变量\(x^{(i)}\)决定的\(y^{(i)}\)的概率分布(即在不同\(x^{(i)}\)取值下的\(y^{(i)}\)出现的概率)
现在考虑给定全部训练样本的\(x^{(i)}\)构成的矩阵\(X=(x^{(1)},\cdots,x^{(m)})^T\),以及全部训练样本的真实输出\(y=(y^{(1)},\cdots,y^{(m)})^T\)
我们可以用下面这个式子表示模型在给定输入X时,正确输出y的概率:
\[P(y|X;\theta)=\prod_{i=1}^mp(y^{(i)}|x^{(i)};\theta)
\]
这就是似然估计:\(L(\theta)=P(y|X;\theta)\),线性回归的优化目标便是:
\[\arg \max_\theta L(\theta)
\]
令对数似然为:
\[l(\theta)=\log(L(\theta))=\sum_{i=1}^m \log(p(y^{(i)}|x^{(i)};\theta))
\]
\[=\sum_{i=1}^m \log(\frac 1 {\sqrt{2\pi}\sigma}\exp(-\frac {(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}))
\]
\[=m\log(\frac 1 {\sqrt{2\pi}\sigma})+\sum_{i=1}^m (-\frac {(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2})
\]
优化目标等价于:
\[\arg\max_\theta l(\theta)
\]
进一步,等价于:
\[\arg\min_\theta \sum_{i=1}^m \frac {(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}
\]
其中,\(\sigma\)是常数,消掉,即可得到:
\[\arg\min_\theta \frac 1 2 \sum_{i=1}^m (y^{(i)}-\theta^Tx^{(i)})^2
\]
这就解释了为何线性回归的损失函数为均方差了
逻辑回归:交叉熵误差函数
由于逻辑回归的假设函数可以表示为\(h_\theta(x)=P(y=1|x;\theta)\),从而
\[p(y^{(i)}=1|x^{(i)};\theta)=h_\theta(x^{(i)})
\]
(\(y^{(i)}=1\)的概率分布,即,给定输入\(x^{(i)}\),真实分类为1,分类正确的概率)
\[p(y^{(i)}=0|x^{(i)};\theta)=1-h_\theta(x^{(i)})
\]
(\(y^{(i)}=0\)的概率分布,即,给定输入\(x^{(i)}\),真实分类为0,分类正确的概率,该式可以视作一个伯努利分布)
\[p(y^{(i)}|x^{(i)};\theta)=[h_\theta(x^{(i)})]^{y^{(i)}}[1-h_\theta(x^{(i)})]^{1-y^{(i)}}
\]
(分类正确的概率分布,即,给定输入\(x^{(i)}\),分类正确的概率)
此时,其似然估计为
\[L(\theta)=\prod_{i=1}^m p(y^{(i)}|x^{(i)};\theta)
\]
对数似然为:
\[l(\theta)=\sum_{i=1}^m \log (p(y^{(i)}|x^{(i)};\theta))
\]
\[=\sum_{i=1}^m y^{(i)}\log (h_\theta(x^{(i)}))+(1-y^{(i)})\log (1-h_\theta(x^{(i)}))
\]
所以逻辑回归的优化目标为
\[\arg \max_{\theta}L(\theta)
\]
等价于
\[\arg \max_{\theta}l(\theta)
\]
等价于
\[\arg \max_{\theta}\sum_{i=1}^m y^{(i)}\log (h_\theta(x^{(i)}))+(1-y^{(i)})\log (1-h_\theta(x^{(i)}))
\]
等价于
\[\arg \min_{\theta}\sum_{i=1}^m [-y^{(i)}\log (h_\theta(x^{(i)}))-(1-y^{(i)})\log (1-h_\theta(x^{(i)}))]
\]
这就解释了为什么逻辑回归的误差函数是交叉熵了
牛顿法求解参数
牛顿法求单调函数零点
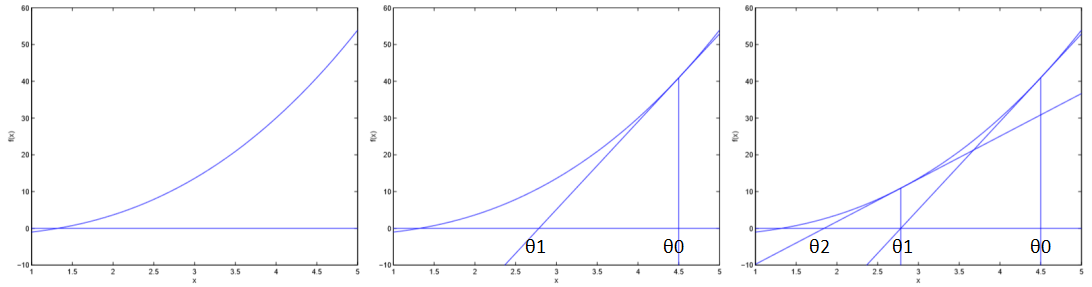
如图,设函数\(f(\theta)\)在某一区间内单调递增,求\(f(\theta)\)在该区间内的一个零点。
首先随机初始化\(\theta^0\),之后每次作\(f(\theta)\)在\((\theta^i,f(\theta^i))\)这一点的切线,切线交x轴于\(\theta^{i+1}\),以此类推,如上图所示
容易看出,
\[f'(\theta^i)=\frac {f(\theta^{i})}{\theta^{i}-\theta^{i+1}}
\]
从而得到
\[\theta^{i+1}=\theta^i-\frac {f(\theta^i)}{f'(\theta^i)}
\]
于是迭代过程可以表示为:
Repeat{
\(\theta:=\theta-\frac {f(\theta)}{f'(\theta)}\)
}
牛顿法最优化一元函数
牛顿法也可以最优化一元函数\(l(\theta)\),一元函数\(l(\theta)\)最大时\(l'(\theta)=0\),因此可以通过用牛顿法寻找\(l'(\theta)\)的零点来找到最优点
Repeat{
\(\theta:=\theta-\frac {l'(\theta)}{l''(\theta)}\)
}
牛顿法最优化损失函数
损失函数的优化目标是使得\(l(\theta)\)取到最大值,此时\(\nabla_\theta l(\theta)=0\),此时需要将上面的方法扩展到n+1元函数\(l(\theta)(\theta \in\mathbb R ^{n+1})\)上
Repeat{
\(\theta:=\theta-H^{-1}\nabla_\theta l(\theta)\)
}
其中,Hessian矩阵\(H\in \mathbb R^{(n+1)\times (n+1)}\)
\[(H)_{i,j}=\frac {\partial^2l}{\partial \theta_i\partial \theta_j}
\]
当参数n比较小的时候,牛顿法的收敛速度明显快于批量梯度下降法,但n过大时,每次迭代都要重新计算一次hessian矩阵及其逆,牛顿法更慢



