机器学习(Andrew Ng)学习笔记(第16~18章)

高斯分布实现异常检测

单变量高斯分布实现异常检测

模型描述

在单变量高斯分布中，对于m组、n种特征的数据，假设其所有特征都是相互独立的，\(P(x|\mu;\sigma^2)\)是数据x正常的概率，那么

\[P(x|\mu;\sigma^2)=P(x_1|\mu_1;\sigma_1^2)\cdots P(x_n|\mu_n;\sigma_n^2) \]

其中

\[P(x_i|\mu_i;\sigma_i^2)=\frac 1 {\sqrt{2\pi}\sigma_i}\exp(-\frac {(x_i-\mu_i)^2}{2\sigma^2}) \]

异常检测过程中，需要确定一个阈值\(t\)，\(P(x|\mu;\sigma^2)>t\)则表明数据点是正常的，反之则为异常。

参数求解

\[\mu_t=\frac 1 m \sum_{i=1}^m x_t^{(i)} \]

\[\sigma_t^2=\frac 1 m \sum_{i=1}^m (x_t^{(i)}-\mu_t)^2 \]

注意，训练过程中，允许训练集中出现少量异常点

特征转换

数据点的某些特征可能不是完美的高斯分布曲线，为了接近高斯分布，可以用对数函数、幂函数等使该特征的分布曲线接近高斯分布

选取阈值的评价标准

假设初始有10000组正常数据点(可能其中包含少量异常数据点)，20个已知的异常点，首先将这些数据按60%,20%,20%比例划分为训练集、交叉验证集、测试集

• 训练集：6000组正常点

• 交叉验证集：2000组正常点，10组异常点

• 测试集：2000组正常点，10组异常点

注意：这里的训练集、交叉验证集、测试集中的数据是完全不重复的

在选取阈值的过程中，一般使用F1 Score作为评价标准：

\[Precision=\frac {TP}{TP+FP} \]

\[Recall=\frac {TP}{TP+FN} \]

\[F_1=2\frac {Precision·Recall}{Precision+Recall} \]

用训练集训练好模型后，首先从小到大枚举阈值，对于每种阈值，使用交叉验证集计算F1 Score，然后选F1 Score最大的阈值作为最终阈值。

最后，用测试集的F1 Score来评价模型在真实环境中的性能。

多变量高斯分布实现异常检测

在单变量高斯分布中，有假设：所有特征都是相互独立的。然而在实际生活中，许多特征之间是互相相关的

例如机房里CPU的耗电量与负载是正相关的，不能单一从CPU耗电量或负载来评价CPU是否异常。然而，若CPU耗电量与负载的比值明显增大，则CPU是异常的。

这时，可以考虑对原始数据构造新的特征：CPU耗电量/负载，再使用单变量高斯分布建模。然而手动构造特征费时费力，于是可以考虑采用多变量高斯分布模型。

模型描述

多变量高斯分布模型中，有假设：一些变量之间存在有相关性

\[P(x|\mu;\Sigma)=\frac 1 {(2\pi)^{\frac n 2}\sqrt{\det(\Sigma)}}\exp(-\frac 1 2 (x-\mu)^T\Sigma^{-1}(x-\mu)) \]

其中，\(\mu=(\mu_1,\cdots,\mu_n)^T=\frac 1 m \sum_{i=1}^m x^{(i)}\)表示n个特征的均值。\(\Sigma\)是x均值归一化后的协方差矩阵：

\[\Sigma=\frac 1 m \sum_{i=1}^m(x^{(i)}-\mu)(x^{(i)}-\mu)^T \]

类似单变量高斯分布模型，这里也要选取一个阈值\(t\)，\(P(x|\mu;\Sigma)>t\)则表明数据点是正常的，反之则为异常。

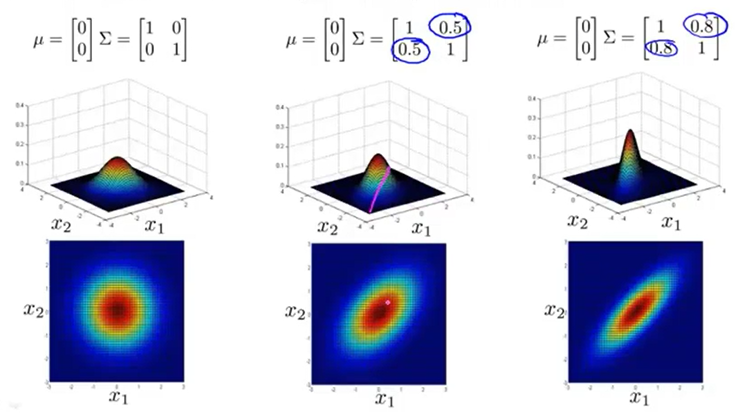
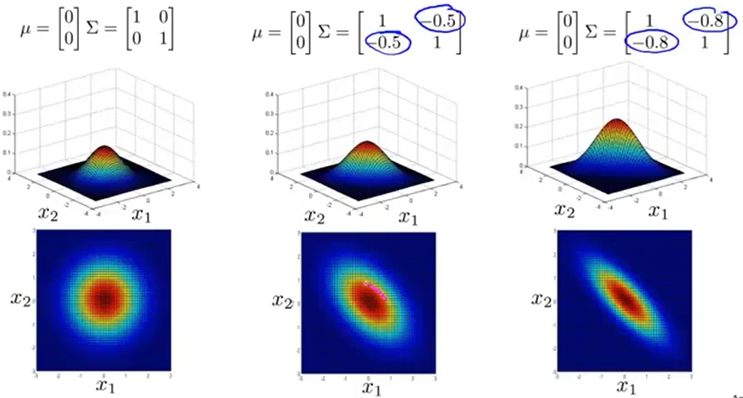
从以上对比中可以看出协方差矩阵对多变量高斯分布的影响。协方差矩阵中第i行第j列元素的绝对值越大，表明特征i和特征j的相关性越大；当协方差矩阵为对角阵时，高斯分布是轴对称的，此时与单变量高斯分布一样

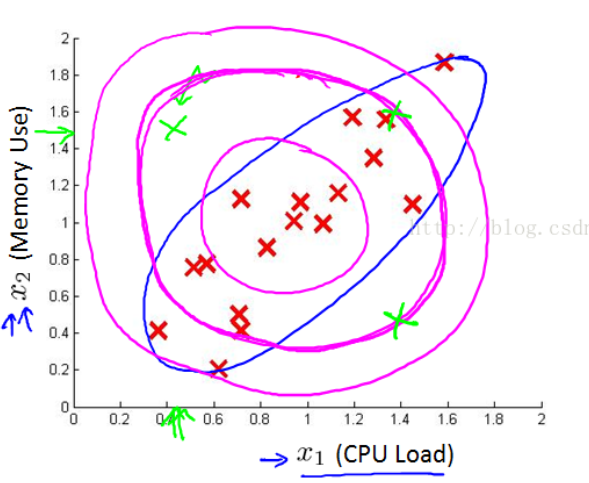
由于单变量高斯分布永远是轴对称的(上图粉色)，而多变量高斯分布的等高线对称轴与坐标轴可以有夹角(上图蓝色)，因此在上图这样的数据点分布情况下，多变量高斯分布可以更好的拟合。

单变量高斯分布 vs. 多变量高斯分布

当特征数量n比较小时，可以直接使用多变量高斯分布，节约大量手动提取特征的时间

当特征数量n非常大时，不能使用多变量高斯分布(此时计算协方差矩阵等运算量太大)，只能考虑手动提取特征，使用单变量高斯分布。

推荐系统

问题描述

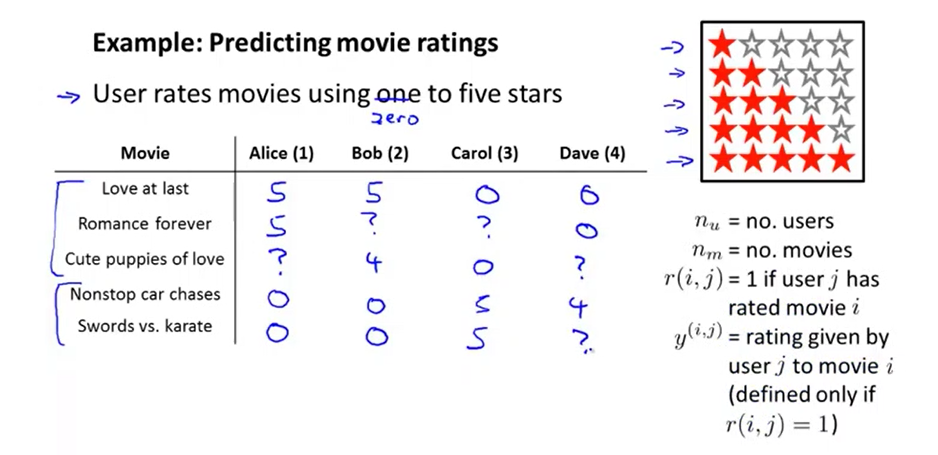
如上图，现有\(n_u\)个用户，\(n_m\)个电影，其中一些用户看过了一些电影，给它们打了分，分数为0~5。\(R(i,j)=1\)表示用户j看过并给电影i打了分，\(y^{(i,j)}\)为用户j对电影i的评分

基于内容的推荐算法

假设现在用\(n_f\)种特征来描述每个电影的内容。每个电影已有一个向量\(x^{(i)}=(1,x_1^{(i)},\cdots,x_{n_f}^{(i)})\)，那么我们可以设法对每个用户求出一个参数\(\theta^{(j)}=(\theta_0^{(j)},\cdots,\theta_{n_f}^{(j)})\)来表示每个用户对电影内容的喜好程度。则用户i对电影j的评分可以用以下模型估计：

\[y^{(i,j)}=\theta^{(j)T}x^{(i)} \]

这是一个线性回归模型：

\[\arg\min_{\theta^{(1)},\cdots,\theta^{(n_u)}}\frac 1 2 \sum_{i,j;R(i,j)=1}(\theta^{(j)T}x^{(i)}-y^{(i,j)})^2+\frac \lambda 2 \sum_{j=1}^{n_u}\sum_{k=1}^{n_f}(\theta_k^{(j)})^2 \]

协同过滤算法

实际上，描述每个电影特征的向量\(x^{(i)}\)并非已知的，协同过滤算法，其实就是在上面的优化目标里，把\(x^{(i)}\)也当成了需要求解的参数：

\[\arg\min_{\theta^{(1)},\cdots,\theta^{(n_u)};x^{(1)},\cdots,x^{(n_m)}}\frac 1 2 \sum_{i,j;R(i,j)=1}(\theta^{(j)T}x^{(i)}-y^{(i,j)})^2+\frac \lambda 2 \sum_{j=1}^{n_u}\sum_{k=1}^{n_f}(\theta_k^{(j)})^2+\sum_{i=1}^{n_m}\sum_{k=1}^{n_f}(x_k^{(i)})^2 \]

然后直接用梯度下降求解参数：

\[\frac {\partial J}{\partial x_k^{(i)}}=\sum_{j:R(i,j)=1}(\theta^{(j)T}x^{(i)}-y^{(i,j)})\theta_k^{(j)}+\lambda x_k^{(i)} \]

\[\frac {\partial J}{\partial \theta_k^{(j)}}=\sum_{i:R(i,j)=1}(\theta^{(j)T}x^{(i)}-y^{(i,j)})x_k^{(i)}+\lambda\theta_k^{(j)} \]

低秩矩阵向量化

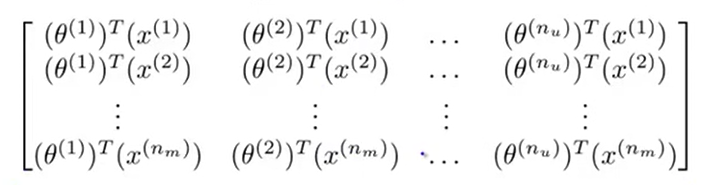
我们用协同过滤算法求出所有参数\(\theta^{(j)},x^{(i)}\)后，用这些参数预测出的用户打分矩阵\(Y=(y^{(i,j)})_{n_m\times n_u}\)，由线性代数知识易知\(r(A)=1\)，且：

\[Y=\begin{pmatrix}x^{(1)T}\\ \vdots\\ x^{(n_m)T}\end{pmatrix}(\theta^{(1)},\cdots,\theta^{(n_u)}) \]

均值归一化

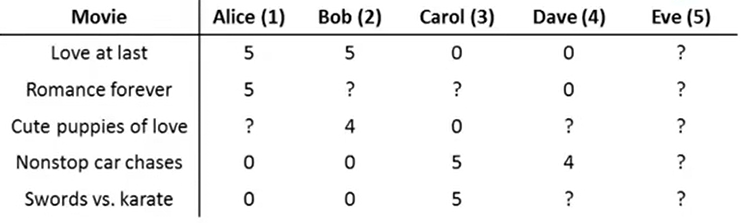
实际上，往往会有一些用户(假设为用户j)没有对任何电影作过打分，此时，若初始时这些没打过分的\(y^{(i,j)}=0\)，受优化目标里正则化项和损失函数部分的影响，最终\(\theta^{(j)}=0\)，使得对于任意的电影\(x^{(i)},\theta^{(j)T}x^{(i)}=0\)，这样得到的预测结果是没有意义的。

均值归一化，即首先求得每个电影i的打分平均值

\[\mu^{(i)}=\frac {\sum_{j;R(i,j)=1}y^{(i,j)}}{\sum_{j;R(i,j)=1}1} \]

然后，\(\forall i,j(R(i,j)=1)\)，\(y^{(i,j)}:=y^{(i,j)}-\mu^{(i)}\)

再完成协同过滤算法，最终预测出的打分，加上对应的均值即可。这样，若用户j没有对任何电影打过分，也能得到一个预测结果：\((\mu^{(1)},\cdots,\mu^{(n_m)})\)。

大规模机器学习

随机梯度下降

之前实现的所有梯度下降算法都属于批量梯度下降(batch gradient descend,BGD)，因为每一次梯度下降都要遍历一遍所有数据，速度太慢。

而在随机梯度下降(stochastic gradient descend)中，首先对所有数据random shuffle，然后依次遍历每个数据\(x^{(i)}\)，依次求出

\[\frac {\partial J(\theta,x^{(i)})}{\partial \theta_t} \]

每遍历一个数据，就用这组偏导数梯度下降一次。

在随机梯度下降算法中，由于每次梯度下降都是朝着单个数据点损失函数下降最快的方向移动，是各自为政，因此随机梯度下降算法表现不稳定，但是速度比批量梯度下降快很多。

Mini-batch随机梯度下降

Mini-batch随机梯度下降(mini-batch stochastic gradient descend)介于随机梯度下降和批量梯度下降之间，首先对所有数据random shuffle，然后每次迭代时，遍历mini-batch size个数据\(x^{(i)},\cdots,x^{(i+b-1)}\)，求出

\[\frac 1 b \sum_{j=i}^{i+b-1}\frac {\partial J(\theta,x^{(j)})}{\partial \theta_t} \]

然后用这组偏导数梯度下降一次。

由于这种梯度下降，每次下降是朝着使一组mini-batch的损失函数之和下降最快的方向移动的，所以比随机梯度下降更稳定；由于每次迭代只访问了mini-batch个数据，所以比批量梯度下降速度更快。

batch-size的大小，一般介于2到100之间

在线学习

在网站中，一般会源源不断地实时产生一系列训练样本给学习模型，而非预先一次性全部提供给学习模型。因此需要使用在线学习。

在线学习里，每次给出一个全新的样本\(x\)，然后用

\[\frac {\partial J(\theta,x)}{\partial \theta_t} \]

来更新全部参数

在线学习还可以随着用户偏好的缓慢变化而不断改变参数

Map Reduce

在梯度下降中，每次迭代需要求出

\[\frac 1 m \sum_{i=1}^m\frac {\partial J(\theta,x^{(i)})}{\partial \theta_t} \]

Map Reduce就是在每次迭代中，将和式拆成若干大小相同的部分\(\sum_{i=t}^{t+b-1}\frac {\partial J(\theta,x^{(i)})}{\partial \theta_t}\)，每一部分交给一个计算单元计算，全部计算单元计算完成后将结果回传给中心汇总，这样做可以将梯度下降过程并行化，从而提高运算速度。

应用举例：照片OCR

OCR Pipeline

OCR Pipeline:

• 1.文字区域检测

• 2.字符分割

• 3.字符分类

滑动窗口

为了检测到文字区域，首先训练一个分类器检测固定大小a*b的图片中是否包含文字。然后用不同大小(比例仍为a:b)的滑动窗口，从照片左上方向右移动，扫描一行，然后略向下移动，重新从左到右扫描一行，以此类推，最终可以得到若干个包含文字的窗口区域，用灰度图表示照片中每个区域包含文字的概率。再用膨胀运算对这个灰度图处理，便可提取出所有文字区域。

再训练一个分类器检测固定大小a*b的图片中是否存在两个文字分割的地方。然后用固定大小(比例为a:b)的滑动窗口从左到右扫描，确定出所有字符分割处，便可实现字符分割

获得更多数据

为了提高模型准确率，一般需要获得更多的数据。可以人造新的数据，或者在原有数据基础上扩充数据(本例中可以考虑添加噪声、仿射变换等做法)，但扩充数据的方法必须保证，新的数据的特点是有可能在实际环境中出现的。

确定机器学习模型的瓶颈

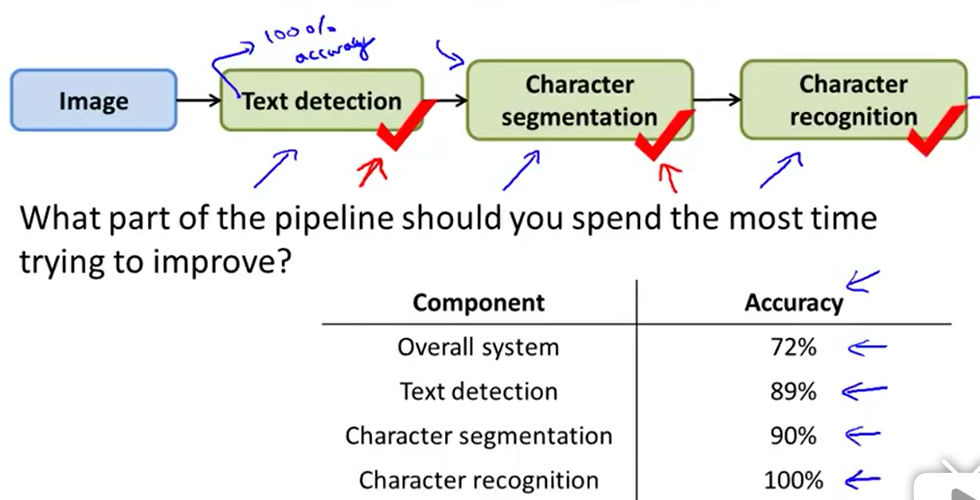
为了确定下一步优化模型中的哪个部分，对整个模型准确率提升最大，可以这样操作：

• 1.画出模型的工作流程

• 2.从第一个部件(图例中是文字检测)开始，用人工替换该部件，保证这一部分准确率为100%，然后记录替换后整个模型的性能

• 3.观察在替换哪个部件后，准确率提升幅度最大(图例中是文字检测)，就首先优化这一部分