MIT线性代数公开课学习笔记第16~20课

十六、投影矩阵和最小二乘

给出\(n\)组\(m-1\)个自变量的数据点(用\(n\times m\)大小的矩阵\(A\)表示，其中第一列均为1，代表常数项)，以及它们的真实取值(用n维列向量\(b\)表示)，现在需要用一个\(m-1\)元未知数的线性方程来拟合这组数据点。可以用非齐次线性方程组\(AX=b\)表示。

一般来说这个方程组是无解的，即\(b\notin C(A)\)，我们需要找到一个近似的\(\hat b,\hat X\)，使得\(A\hat X=\hat b\)。其中\(b_i\)是第\(i\)个数据点的真实取值，\(\hat b_i\)是第\(i\)个数据点通过拟合直线的近似取值，如下图所示：

在第十五课已经讲过，最小二乘法的损失函数是均方差函数，即：

\[\mathrm{minimize}\ \ \sum_{i=1}^m(b_i-\hat b_i)^2 \]

换言之：

\[\mathrm{minimize}\ \ \|b-\hat b\|^2 \]

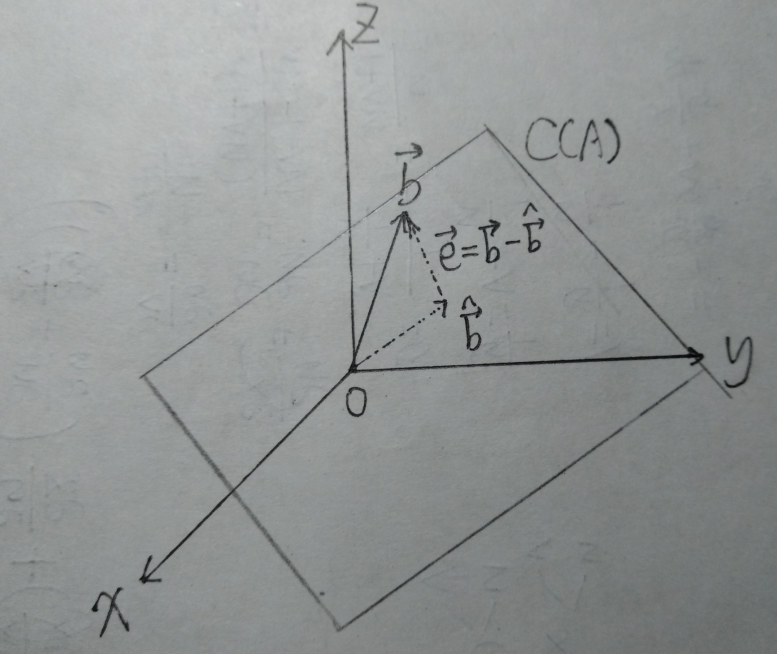
为直观起见，这里的\(\mathrm{dim}C(A)=2\)，则\(b\)投影到\(C(A)\)上的向量\(\hat b\)如图所示，显然\(e=b-\hat b,e\perp C(A)\)，因此此时\(\|e\|=\|b-\hat b\|\)是最小的。

根据第十五节的知识，我们可以令投影矩阵\(P=A(A^TA)^{-1}A^T\)，则：

\[\hat b=Pb=A(A^TA)^{-1}A^Tb \]

\[A\hat X=\hat b \]

上式左右同时左乘\(A^T\)：

\[A^TA\hat X=A^TA(A^TA)^{-1}A^Tb=A^Tb \]

根据这个非齐次线性方程组便可以解出\(\hat X\)，也就能得到这个拟合的直线方程了。

十七、正交矩阵和Gram-Schmidt正交化

正交矩阵和Gram-Schmidt正交化在国内的各类线代教材中都有出现，这里不做过多赘述。

这里值得一提的是，前\(t-1\)个线性无关向量\(\alpha_1\cdots \alpha_{t-1}\)已正交化为\(\beta_1\cdots \beta_{t-1}\)，正交化第\(t\)个向量\(\alpha t\)的过程，就是将其投射到\(C(\beta_1\cdots \beta_{t-1})\)这个空间中，然后获得误差向量的过程。

如上图，若已获得两个正交化的向量\(\beta_1,\beta_2\)，则首先将\(\alpha_3\)投射到\(C(\beta_1,\beta_2)\)得到\(\mathrm{Prj}_{C(\beta_1,\beta_2)}\alpha_3\)

则

\[\beta_3=\alpha_3-\mathrm{Prj}_{C(\beta_1,\beta_2)}\alpha_3=\alpha_3-\mathrm{Prj}_{\beta_1}\alpha_3-\mathrm{Prj}_{\beta_2}\alpha_3 \]

由十五课的投影相关的内容可得

\[\beta_3=\alpha_3-(\alpha_3,\beta_1)\frac{\beta_1}{\|\beta_1\|}-(\alpha_3,\beta_2)\frac{\beta_2}{\|\beta_2\|} \]

十八、行列式性质

国内线代教材包含了此课中的所有内容，此处不作过多赘述。

十九、行列式公式

根据行列式的性质，将三阶行列式按第一行拆分，如下图：

然后对每个行列式，将其按第二行拆分，以此类推，最终可以得到：

类似地，对于\(n\)阶行列式\(\mathrm{det}(a_{i,j})_{n\times n}\)而言，可以将其拆分为

\[\sum(-1)^x\mathrm{Permutation}\{1,2,\cdots,n\} \]

其中\(\{i,j,\cdots,l\}\)表示的是\(a_{1,i}a_{2,j}\cdots a_{n,l}\),\(x\)是序列\(\{i,j,\cdots,l\}\)的逆序对个数，\(\mathrm{Permutation}\{1,2,\cdots,n\}\)表示的是1到n的全排列

如果我们把其中含\(a_{i,j}\)的项全部提出来，就能得到\(a_{i,j}\)对应的代数余子式\(A_{i,j}\)

二十、克拉默法则

国内线代教材包含了克拉默法则相关的内容，此处不作过多赘述。

值得一提的是二阶(三阶)行列式的值与面积(体积)的关系。

对于一个二阶矩阵A

\[A=\begin{pmatrix}a & b\\c & d\end{pmatrix} \]

而言，\(|\mathrm{det}(A)|\)就是如下平行四边形的面积：

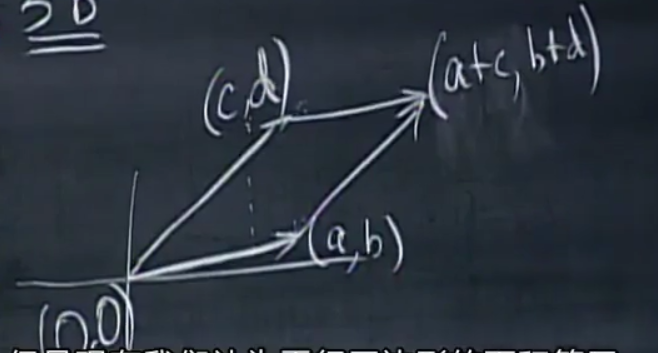
实际上这和叉积是完全相同的：

\[|det(A)|=|ad-bc|=|\{a,b\}\times \{c,d\}| \]

对于一个三阶矩阵A

\[A=\begin{pmatrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{pmatrix} \]

而言，\(|\mathrm{det}A|\)就是如下图所示的平行六面体的体积

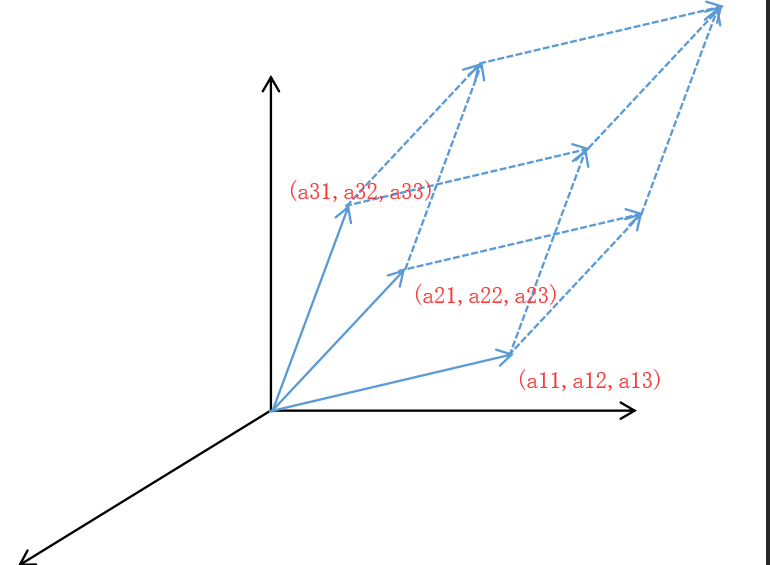
这符合混合积的定义：

\[V=|(\{a_{1,1},a_{1,2},a_{1,3}\}\times \{a_{2,1},a_{2,2},a_{2,3}\})·\{a_{3,1},a_{3,2},a_{3,3}\}| \]

而且二阶(三阶)行列式的性质也有几何意义。如对于三阶行列式A的某一行乘以2得到A'，则A'=2A，相当于是对应的向量长度乘2，则该平行六面体体积也乘2