MIT线性代数公开课学习笔记第6~10课(列空间和零空间,求解Ax=0,求解Ax=b,线性相关性、基、维数,四个基本子空间)
六、列空间和零空间
本节课介绍了两种构建线性子空间的方法:
1、列空间(矩阵的列向量组的线性组合构成的集合)
2、零空间(齐次线性方程组的所有解构成的集合)
1、向量空间的进一步讨论
在第五节课我们已经知道,\(\mathbb{R}^3\)内任何过原点的直线或平面上的所有向量构成一个向量空间。
考虑一条过原点的直线上所有向量构成的向量空间\(L\)和一个过原点的平面上所有向量构成的向量空间\(P\),如下图所示:

对于集合\(V=P\cup L\)而言,它不是一个向量空间,因为任取非零向量\(\alpha\in P,\beta\in L,\alpha+\beta\notin V\),这在几何上看是非常直观的。
对于集合\(V=P\cap L\)而言,它是一个向量空间,因为任取非零向量\(\alpha\in (P\cap L),\beta\in (P\cap L)\),\(\alpha+\beta\in P,\alpha+\beta\in L\),从而\(\alpha+\beta\in (P\cap L)\)
2、矩阵列空间的构造方法
考虑构造\(3\times 2\)矩阵\(A\)的列空间\(C(A)\),或者说通过\(A\)的两个三维列向量构造\(\mathbb{R}^3\)的一个子空间\(C(A)\),其中
\(A\)的列空间\(C(A)\)为\(A\)的两个三维列向量通过所有的线性组合产生的向量构成的集合。
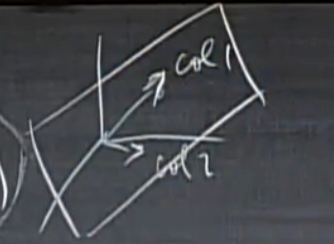
从几何角度看,这就是\(\mathbb{R}^3\)空间中,两个列向量所在的平面(显然该平面过原点)上的所有向量构成的集合。
如果这里的两个列向量是线性相关的,显然构造出来的列空间是过原点的一条直线上的所有向量构成的集合。
3、矩阵列空间的维度

\(Ax=b\)有解,当且仅当\(b\)是\(A\)的若干个列向量的线性组合,或者说\(b\)属于\(A\)的列空间
\(A\)的列空间\(C(A)\)的维度\(\mathrm{dim} C(A)\)=\(r(A)\)(\(A\)的列向量的秩),因为对于A的列向量构成的向量组而言,其中的一个极大线性无关组的线性组合足以构成\(\mathrm{dim}C(A)\),其他向量均可由这个极大线性无关组线性表示,它们不会对最终的列空间产生任何贡献。
\(A\)的列向量组的任一个极大线性无关组均能作为\(\mathrm{dim}C(A)\)的一组基
4、矩阵零空间
对于一个大小为\(n\times m\)的矩阵\(A\),其对应的齐次线性方程组\(Ax=0\)的所有解构成的集合就是矩阵\(A\)的零空间(the null space)\(N(A)\),其任意一个基础解系均能作为\(N(A)\)的一组基。
考虑\(Ax=0\)的两组解\(x_1,x_2\in N(A)\),\(A(x_1+x_2)=Ax_1+Ax_2=0\),\(A(kx_1)=kAx_1=0\),因此零空间对于加法和数乘运算是封闭的。
然而\(Ax=b(b\neq 0)\)的所有解构成的集合不是一个线性空间,因为\(A\cdot 0\neq b\),而线性空间必须包含零向量(或者说,因为当\(Ax_1=b,Ax_2=b\)时,\(A(x_1+x_2)=2b\neq b\))。实际上,\(Ax=b(b\neq 0)\)的所有解构成的集合是不过原点的一个超平面(在\(\mathbb{R}^3\)中是不过原点的直线或平面)。
七、求解Ax=0:主变量、特解
对于一个\(n\times m\)矩阵\(A\),求解\(Ax=0\)的过程如下:
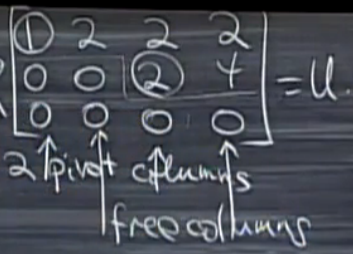
- (1)通过初等行变换将\(A\)变成上阶梯型矩阵\(U\),其中,\(U\)每一行第一个非零元素称为主元(pivot)(如图中被圈上的元素)。\(A\)的秩(rank)就是\(U\)中主元的个数。含有主元的列被称为主列(pivot column),不含有主元的列被称为自由列(free column)。
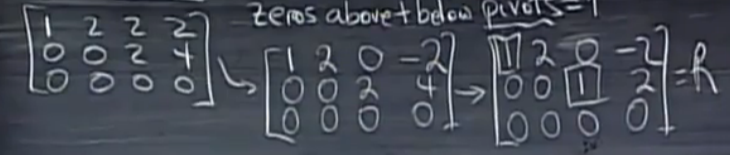
-
(2)将\(U\)化为行简化阶梯形矩阵\(R\)(reduced row echelon form),\(R\)中每个主列除主元外其他元素均为0,且每个主元均为1。首先从最后一行开始,用该行\(i\)对前\(i-1\)行作初等行变换以消去主列上除主元外的其他元素(如图中第一步所示)。然后对每一行乘以一个系数,使得该行的主元变为1(如图中第二步所示)。
-
(3)设共有\(t\)个自由列(显然\(t=m-r(A)\),也就是\(m\)个未知数减去\(r(A)\)个主列对应的未知数),分别让每个自由列对应的未知数取1,其余自由列对应未知数取0,把这组值代入方程组中,回代得到\(Ax=0\)的一个特解\(x_i\),以此类推,得到\(Ax=0\)的一个基础解系\(\{x_1,x_2,\cdots ,x_t\}\)
-
(4)\(Ax=0\)的通解就是其基础解系\(\{x_1,x_2,\cdots ,x_t\}\)的线性组合构成的集合。或者说是基础解系中这\(t\)个线性无关的向量线性组合构成的一个线性空间。
考虑一个\(n\times m\)的行简化阶梯形矩阵\(R\),不失一般性,设\(R=\begin{pmatrix}I_{r(A)} & F_{r(A)\times (m-r(A))} \\ 0 & 0\end{pmatrix}\),则
因此\(\begin{pmatrix}-F_{r(A)\times (m-r(A))}\\I_{(m-r(A))}\end{pmatrix}\)的每个列向量是原方程组的一个特解,而且显然这些列向量是线性无关的,因此它们构成了这个方程组的一个基础解系。换言之,该矩阵的列空间就是\(A\)的零空间。
八、求解Ax=b:可解性和解的结构
1、Ax=b有解的条件
非齐次线性方程组\(Ax=b\)有解,当且仅当:
(1)\(b\)可以由\(A\)的列向量组线性表示,或者说\(b\in C(A)\)
或者,
(2)对于\(A\)的行向量组的任意一个得到零向量的线性组合,对\(b\)按这个线性组合其中各个元素,得到的是0
2、Ax=b的解的结构
\(Ax=b\)的解=\(Ax=0\)的通解(\(A\)的零空间\(N(A)\))+\(Ax=b\)的一个特解\(x_p\)(particular solution)

考虑\(\mathbb{R}^4\)空间中的一个非齐次线性方程组的通解\(x_c\),其对应齐次线性方程组基础解系含两个列向量(\(\mathrm{dim}N(A)=2\))
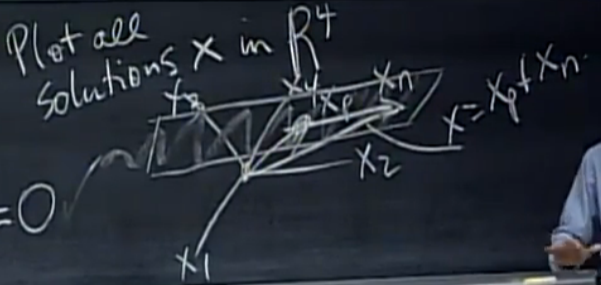
从几何角度看,\(N(A)\)是一个二维平面,将这个平面平移至过向量\(x_p\)的终点,\(x_c\)是起点为原点,终点在平移过后的\(N(A)\)平面上的所有向量。
3、Ax=b与A的秩之间的关系
设\(A\)为\(n\times m\)矩阵。
(1)A的列秩=m,\(n>m\)
此时方程组无自由变量(\(A\)的零空间\(N(A)=\{0\}\),\(\mathrm{dim}N(A)=0\)),行简化阶梯形矩阵\(R=\begin{pmatrix}I \\ 0 \end{pmatrix}\)。
通过消元得到\(m\)个主元,若\(Ax=b\)有解,则只能有唯一解;否则\(Ax=b\)无解。
(2)A的行秩=n,\(n<m\)
最终得到的行简化阶梯形矩阵\(R\)中每一行不全为0,有\(n\)个主元。
因此\(\forall b\in \mathbb{R}^n,Ax=b\)均有无穷多解。
(3)\(n=m=r(A)\)
此时\(A\)的行简化阶梯形矩阵\(R=I_n\),且\(A\)可逆,\(\forall b\in \mathbb{R}^n\),\(Ax=b\)均有解
(4)\(r(A)<n,r(A)<m\)
此时\(\mathrm{dim}N(A)\geq 1\),且行简化阶梯形矩阵中有全零行,因此\(Ax=b\)要么无解,要么有无穷多解。
九、线性相关性、基、维数
1、线性相关、线性无关
国内线代教材中都有线性相关与线性无关的定义,这里不再赘述。
需要注意的是,任何一个包含零向量的向量组都是线性相关的(可以让零向量前的系数取任意非零常数,其他向量系数全部取0)
\(n\)维向量构成的线性无关组中包含的向量个数最多为\(n\)个。对于任意包含\(m\)个向量的向量组\(\alpha_1,\alpha_2,\cdots,\alpha_m\),
该齐次线性方程组的系数矩阵大小为\(n\times m(n < m)\),所以必有自由变量,该方程一定有非零解,所以该向量组必然是线性相关的。
\(\begin{pmatrix}\alpha_1,\alpha_2,\cdots,\alpha_m\end{pmatrix}X=0\)的解空间只有零向量,则这个向量组是线性无关的,反之则这个向量组是线性相关的。
2、生成空间
若干个向量的生成空间是这些向量线性组合得到的所有向量构成的集合。
3、矩阵的秩、主元个数、列空间维度之间的关系
矩阵的秩=主元个数=列空间维度
4、列空间的基
矩阵A的列空间的基是A的列向量组里的任意一个极大线性无关组。
5、零空间的基
矩阵A的零空间的基是齐次线性方程组\(AX=0\)的任意一个基础解系。
6、总结
对于\(n\times m\)的矩阵\(A\)而言,
十、四个基本子空间
本节课介绍了\(n\times m\)的矩阵\(A\)的四种基本子空间:
-
(1)列空间\(C(A)\)
-
(2)零空间\(N(A)\)
-
(3)行空间\(C(A^T)\)(\(A\)的行向量的所有线性组合构成的集合)
-
(4)\(A^T\)的零空间(左零空间)\(N(A^T)\)
其中,\(C(A) \subset \mathbb{R}^n\),\(N(A) \subset \mathbb{R}^m\),\(C(A^T) \subset \mathbb{R}^m\),\(N(A^T) \subset \mathbb{R}^n\)
1、四个基本子空间的维度
\(\mathrm{dim}C(A)=\mathrm{dim}C(A^T)=r(A)\)
\(\mathrm{dim}N(A)=m-r(A),\mathrm{dim}N(A^T)=n-r(A)\)
2、四个基本子空间的基
\(C(A)\)的基就是\(A\)的任意一组主列(pivot columns)
注意:\(A\)的行简化阶梯形矩阵\(R\)的列空间\(C(R)\neq C(A)\),但它们的行空间相同,即\(C(R^T)=C(A^T)\),因为对\(A\)作初等行变换仍是对这些行向量作线性组合
由此可以得到,行空间\(C(A^T)\)的基是\(R\)的前\(r(A)\)个非零行向量
\(N(A)\)的基就是\(AX=0\)的任意一组基础解系
对于左零空间而言,其中任意一个列向量满足\(A^TY=0\),左右同时转置得\(Y^TA=0\),即根据左零空间中的任意一个向量来线性组合\(A\)的行向量可以得到零向量。
\(A\)通过初等行变换变为行简化阶梯形矩阵\(R\)的过程,可以用\(n\)阶可逆方阵\(P\)表示:\(PA=R\),那么\(R\)的最后\(n-r(A)\)个零行对应于,根据\(P\)的最后\(n-r(A)\)行中某一行线性组合\(A\)的行向量。因此:
\(\mathrm{dim}N(A^T)=n-r(A)\)
3、矩阵空间
课程的最后提及了矩阵空间\(\mathbb{R}^{n\times n}\),\(\mathbb{R}^{n\times n}\)是所有n阶实方阵构成的集合,该集合满足加法与数乘的封闭性、线性空间的八条运算律。
矩阵空间的子空间:
-
(1)所有n阶上三角方阵构成的集合
-
(2)所有n阶对称方阵构成的集合
-
(3)所有n阶对角阵构成的集合
很显然(3)是包含于(1)或(2)的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号