MIT线性代数公开课学习笔记第1~5课(方程组的几何解释,矩阵消元,乘法和逆矩阵,LU分解,转置-置换-向量空间)

一、方程组的几何解释

行图像(Row Picture)与列图像(Column Picture)

设\(A\)为\(n\times m\)的矩阵，\(x\)为\(m\)维的列向量，\(b\)为\(n\)维的列向量。考虑如下的等式：

\[Ax=b \]

课程提出了行图像(Row Picture)与列图像(Column Picture)的概念。

在行图像中，\(A\)里第\(i\)行元素\((A_{i,1},A_{i,2},\cdots,A_{i,m})\)与\(b\)的第\(i\)维元素\(b_i\)构成了一个方程

\[A_{i,1}x_1+A_{i,2}x_2+\cdots+A_{i,m}x_m=b_i \]

由于\(x\)中有\(m\)个未知数，因此方程可用\(m\)维空间里的超平面表示(在二维空间中是直线，在三维空间中是平面)。

由于\((x_1,x_2,\cdots,x_m)\)是\((A,b)\)代表的\(n\)个方程构成的方程组的解，因此它可视为是\(m\)维空间里\(n\)个超平面的共同交点的坐标。

在列图像中，\(A\)可视作\(m\)个\(n\)维列向量构成的矩阵\((\alpha_1,\alpha_2,\cdots,\alpha_m)\)，则：

\[Ax=\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_mx_m=b \]

即用\((x_1,x_2,\cdots,x_m)\)来线性组合向量\(\alpha_1,\alpha_2,\cdots,\alpha_m\)从而得到列向量\(b\)

需要注意的是，当\(m=n\)时，只有这\(n\)个列向量线性无关时，对于任意的\(b\)，都能由这些列向量线性表示。

二、矩阵消元

对于\(n\times m\)矩阵\(A\)，其消元的一般步骤为：

对\(A\)作\(t\)次初等行变换，每次行变换可用一个\(n\)阶初等方阵\(E_i\)表示，最终得到行阶梯形矩阵\(U\)，该步骤可用\(PA=U\)表示，其中\(P=E_1E_2 \cdots E_t,|P|=|E_1||E_2|\cdots |E_t|\neq 0\)，即\(P\)为一个可逆方阵

最终得到的矩阵\(U\)可以通过相反的初等行变换变回原来的\(A\)。

\(A=P^{-1}U=(E_1E_2\cdots E_t)^{-1}U=E_t^{-1}E_{t-1}^{-1}\cdots E_1^{-1}U\)

三、乘法和逆矩阵

1、矩阵乘法的四种表示法

矩阵乘法的第一种表示法(常规方法,the regular way)：

对于\(n\times m\)矩阵\(A\)和\(m\times k\)矩阵\(B\)，定义其乘法\(C=AB\)，\(C\)为\(n\times k\)矩阵。其中，

\[c_{i,j}=\sum_{t=1}^m a_{i,t}b_{t,j} \]

我们也可这样表述：
若对\(A\)按行分块为\(\begin{pmatrix}\alpha_1\\ \alpha_2\\ \vdots \\ \alpha_n\end{pmatrix}\)，对\(B\)按列分块为\(\begin{pmatrix}\beta_1,\beta_2,\cdots,\beta_k\end{pmatrix}\)，则\(C=AB\)也可这样表示：

\[C= \begin{pmatrix} \alpha_1\beta_1 & \alpha_1\beta_2 & \cdots & \alpha_1\beta_k\\ \alpha_2\beta_1 & \alpha_2\beta_2 & \cdots & \alpha_2\beta_k\\ \vdots & \vdots & \ddots & \vdots \\ \alpha_n\beta_1 & \alpha_n\beta_2 & \cdots & \alpha_n\beta_k\\ \end{pmatrix} \]

即\(C\)中\((i,j)\)对应元素是\(A\)的第\(i\)行行向量与\(B\)的第\(j\)列列向量的点积

矩阵乘法的第二种表示法(列方法，the column way)：

若对\(B\)按列分块为\(\begin{pmatrix}\beta_1,\beta_2,\cdots,\beta_k\end{pmatrix}\)，对\(C\)按列分块为\(\begin{pmatrix}\gamma_1,\gamma_2,\cdots,\gamma_k\end{pmatrix}\)，则\(C=AB\)也可这样表示：

\[\gamma_i=A\beta_i \]

即\(C\)中第\(i\)列是\(A\)与\(B\)中第\(i\)列列向量的乘积。
换言之，\(C\)中第\(i\)列的列向量是\(A\)的\(m\)个列向量分别按\(\beta_i\)中每个元素加权相加的线性组合

矩阵乘法的第三种表示法(行方法，the row way)：

若对\(A\)按行分块为\(\begin{pmatrix}\alpha_1\\ \alpha_2\\ \vdots \\ \alpha_n\end{pmatrix}\)，对\(B\)按行分块为\(\begin{pmatrix}\beta_1\\ \beta_2\\ \vdots \\ \beta_m\end{pmatrix}\)，对\(C\)按行分块为\(\begin{pmatrix}\gamma_1\\ \gamma_2\\ \vdots \\ \gamma_n\end{pmatrix}\)，则\(C=AB\)也可这样表示：
\(\gamma_i=\alpha_{i,1}\beta_1+\alpha_{i,2}\beta_2+\cdots+\alpha_{i,m}\beta_m\)
即\(C\)中第\(i\)行是\(B\)中\(m\)个行向量分别按\(A\)中第\(i\)行的各元素加权相加的线性组合

矩阵乘法的第四种表示法：

若对\(A\)按列分块为\(\begin{pmatrix}\alpha_1 & \alpha_2 & \cdots & \alpha_m\end{pmatrix}\)，对\(B\)按行分块为\(\begin{pmatrix}\beta_1\\ \beta_2\\ \vdots \\ \beta_m\end{pmatrix}\)，则\(C=\sum_{i=1}^m \alpha_i\beta_i\)

2、矩阵分块

高校线代教材中都有这一知识点，这里不再赘述

3、矩阵求逆

若\(BA=I\)，称\(B\)为\(A\)的左逆矩阵(Left inverse matrix)，若\(AB=I\)，称\(B\)为\(A\)的右逆矩阵(Right inverse matrix)。

若\(A\)为方阵且可逆，则\(A\)的左逆矩阵与右逆矩阵相同，称之为\(A^{-1}\)
若\(A\)不是方阵，则\(A\)的左逆矩阵与右逆矩阵一定不同(因为此时左逆矩阵与右逆矩阵不同型)

可逆矩阵(Invertible matrix)又称为非奇异矩阵(Nonsingular matrix)，其对应行列式不为零。

方阵\(A\)不可逆时，无法找到一个方阵\(B\)，使得\(AB=I\)，或者说使得\(A\)的\(n\)个列向量通过线性组合可以得到\(I\)中每一个列向量。

从几何角度来说，由于\(A\)的\(n\)个列向量是线性相关的，所以这些列向量无法通过线性组合得到\(n\)维空间的所有向量，只能表示\(n\)维空间中某个\(m\)维(\(m< n\))超平面上的向量，也就无法表示单位阵\(I\)中某一列的列向量(这一表述不是非常严谨，仅供感性参考)。

也可这样表述，当\(A\)不可逆时，\(A\)中\(n\)个列向量线性相关，它们可通过线性组合得到零向量。换言之，方程\(Ax=0\)有非零解\(x\neq 0\)，若此时\(A^{-1}\)存在，则\(x=A^{-1}Ax=A^{-1}0=0\)，矛盾。因此\(A^{-1}\)不存在。

4、高斯-约当(Gauss-Jordan)法求矩阵的逆

课程在讲矩阵求逆时顺带提及了这一知识点。

考虑可逆方阵\(A\)：

• (1)将\(A\)与单位阵\(I\)排成矩阵\(M=\begin{pmatrix} A & I\end{pmatrix}\)

• (2)对该矩阵作若干次初等行变换，变为\(M'=\begin{pmatrix} I & I'\end{pmatrix}\)

• (3)此时\(A^{-1}=I'\)

高斯-约当法的原理很简单，对\(M\)作\(t\)次初等行变换可视为对\(M\)左乘一个可逆方阵\(P=E_1E_2\cdots E_t\)，使得\(PA=I\)，则\(P=A^{-1}\)，\(M'=PM=\begin{pmatrix} PA & PI\end{pmatrix}=\begin{pmatrix} I & A^{-1}\end{pmatrix}\)

BTW:高斯-约当法也可直接用于对线性方程组\(Ax=b\)求解(其中\(A\)是可逆方阵)，差别只是把\(M\)右边的\(I\)改为\(b\)，最终得到的\(M'\)右边的列向量就是解向量\(x\)

四、A的LU分解

1、A的LU分解

LU分解是最基本的矩阵分解方法。即使用一个下三角方阵\(L\)(Lower triangulear matrix)和一个上三角矩阵\(U\)(Upper triangular matrix)的乘积\(LU\)表示方阵\(A\)。

LU分解的步骤如下：

• (1)对\(A\)作\(n-1\)回合的初等行变换，第\(i\)回合用\(A\)的第\(i\)行将\(A\)的第\(i\)列中第\(i+1,\cdots ,n\)行元素全部清零，这些步骤可以用若干个下三角的初等方阵\(E_1,\cdots ,E_t\)表示

• (2)令\(P=E_1E_2\cdots E_t,PA=U\)

• (3)\(A=P^{-1}U\)，\(P^{-1}=E_t^{-1}E_{t-1}^{-1}\cdots E_1^{-1}\)也是一个下三角方阵(下三角方阵的逆阵也是下三角方阵)，\(L=P^{-1}\)

2、LU分解算法的时间复杂度分析

考虑方阵

\[A= \begin{pmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n,1} & a_{n,2} & \cdots & a_{n,n} \end{pmatrix}\]

将其消元至上三角矩阵\(U\)步骤如下：

• (1)分别用第一行对第\(2\cdots n\)行作初等行变换，消去第\(2\cdots n\)行的第一列(这里假设\(a_{1,1}\neq 0\)，若\(a_{1,1}=0\)则无法继续进行LU分解)，得到：

\[A'= \begin{pmatrix} a'_{1,1} & a'_{1,2} & \cdots & a'_{1,n}\\ 0 & a'_{2,2} & \cdots & a'_{2,n}\\ \vdots & \vdots & \ddots & \vdots\\ 0 & a'_{n,2} & \cdots & a'_{n,n} \end{pmatrix}\]

该消元过程中，最多需要做\(n-1\)次初等行变换，每次初等行变换要做\(n\)次运算。

• (2)类似地，分别用第二行对第\(3\cdots n-1\)行作初等行变换，消去第\(3\cdots n-1\)行的第二列，该消元过程中，最多需要做\(n-2\)次初等行变换，每次初等行变换要做\(n-1\)次运算。

以此类推，将\(A\)变换为\(U\)需要做的运算次数是：

\(n(n-1)+(n-1)(n-2)+\cdots+1\)

因此\(LU\)分解的时间复杂度是\(O(n^3)\)

实际上运算次数接近于\(\frac 1 3 n^3\)，因为上面的和式可以近似看作积分\(\int_0^n x^2 dx=\frac 1 3 n^3\)

五、转置-置换-向量空间R

1、置换矩阵

置换矩阵是把每一行重新排列过的单位阵。\(n\)阶的置换矩阵共有\(n!\)种(也就是\(n\)阶单位阵\(n\)个行向量全排列的个数)

置换矩阵都是可逆的，而且具有一个很好的性质：\(P^{-1}=P^T\)

2、转置矩阵

国内教材中都有转置矩阵的概念，这里不再赘述。

3、对称矩阵

国内教材中都有对称矩阵的概念，这里不再赘述。

需要注意的是，对于任意一个\(n\times m\)矩阵\(R\)，我们都能通过它构造出一个对称矩阵\(A=RR^T\)。

\[A^T=(RR^T)^T=(R^T)^TR^T=RR^T=A \]

所以\(A\)是对称矩阵。

4、向量空间

向量有最基本的两种运算：

• (1)加法：给出两个向量\(\alpha,\beta\)，向量\(\gamma=\alpha+\beta\)

• (2)数乘：用一个标量\(k\)(scalar)数乘一个向量

向量空间\(V\)是由\(k\)维向量构成的非空集合，该集合中定义了加法和数乘两种运算。这两种运算满足八条运算规则(参见居余马版线性代数P175)，且\(V\)对这两种运算封闭(即运算结果仍属于\(V\))，或者说\(V\)对\(V\)中元素的线性组合是封闭的。

需注意的是，任意一个向量空间\(V\)均包含零向量(若不包含零向量，则用标量0数乘\(V\)中任何一个向量得到零向量，而零向量不属于\(V\)，则\(V\)不是封闭的，从而\(V\)不是向量空间)

全体\(n\)维实向量构成的集合\(\mathbb{R}^n\)都是向量空间。

5、向量子空间

对于一个向量空间\(V\)，若其的一个非空子集\(V'\subset V,V'\)也构成一个向量空间，则称\(V'\)是\(V\)的一个向量子空间。

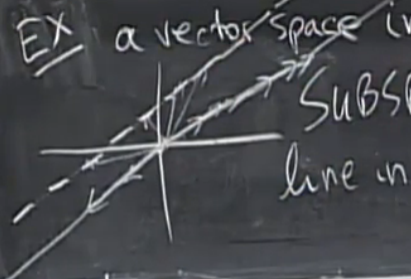
设图中平面上不过原点的虚线为\(L_1\)，过原点的直线为\(L_2\)
对于向量空间\(\mathbb{R}^2\)而言，所有终点在\(L_2\)上的向量构成的集合是\(\mathbb{R}^2\)的子空间，而所有终点在\(L_1\)上的向量构成的集合不是\(\mathbb{R}^2\)的子空间(因为其中任意一个向量数乘0得到的零向量不属于该集合)

向量空间\(\mathbb{R}^2\)有三种子空间：

• (1)\(\mathbb{R}^2\)

• (2)对于任意一条过原点的直线\(L\)，终点在\(L\)上的向量构成的集合

• (3)零向量

\(\mathbb{R}^3\)则有四种子空间：

• (1)\(\mathbb{R}^3\)

• (2)对于任意一条过原点的直线\(L\)，终点在\(L\)上的向量构成的集合

• (3)对于任意一条过原点的平面\(P\)，终点在\(P\)上的向量构成的集合

• (4)零向量

(2)和(3)从几何角度看是非常直观的。

6、矩阵列空间的构造方法

考虑构造\(3\times 2\)矩阵\(A\)的列空间\(C(A)\)，或者说通过\(A\)的两个三维列向量构造\(\mathbb{R}^3\)的一个子空间\(C(A)\)，其中

\[A= \begin{pmatrix} 1 & 3\\ 2 & 3\\ 4 & 1 \end{pmatrix}\]

\(C(A)\)为\(A\)的两个三维列向量通过所有的线性组合产生的向量构成的集合。

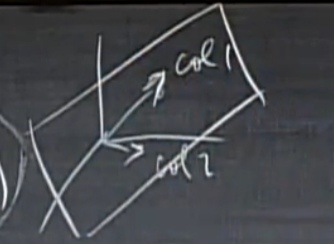
从几何角度看，这就是\(\mathbb{R}^3\)空间中，两个列向量所在的平面(显然该平面过原点)上的所有向量构成的集合。

如果这里的两个列向量是线性相关的，显然构造出来的列空间是过原点的一条直线上的所有向量构成的集合。