15. 时间空间效率的平衡（4）

题一：【丑数】

 把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

 分析：自己写了一个，算法复杂度太大了——写一个判断是否是丑数的函数，然后依次判断

public class Solution {
    public int GetUglyNumber_Solution(int index) {
        if(index<=0) return 0;
        int count=1;//计数
        int res = 1;
        while(count<=index){
            if(isUgly(res)){
                if(count==index) return res;
                count++;
                res++;
            }else{
                res++;
            }
        }
        return 0;
    }
    public boolean isUgly(int num){
        if(num==1) return true;
        int res = num;
        while(num!=0){
            if(num%2==0){
                num = num/2;
            }else if(num%3==0){
                num = num/3;
            }else if(num%5==0){
                num = num/5;
            }else{
                return false;
            }
            if(num==1) return true;
        }
        return false;
    }
}

分析：DP

import java.lang.Math;
public class Solution {
    public int GetUglyNumber_Solution(int index) {
        if(index<=0) return 0;
        if(index<7) return index;
        //后面的丑数是有前一个丑数乘以2，3，5中的一个得来。因此可以用动态规划去解
        int t2=0,t3=0,t5=0;
        int[] dp = new int[index];
        dp[0] = 1;
        for(int i=1;i<index;i++){
            dp[i] = Math.min(dp[t2]*2,Math.min(dp[t3]*3,dp[t5]*5));
            if(dp[i]==dp[t2]*2) t2++;
            if(dp[i]==dp[t3]*3) t3++;
            if(dp[i]==dp[t5]*5) t5++;
        }
        return dp[index-1];
    }
}

 

题二：【第一个只出现一次的字符位置】

 在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）。

分析：只能暴力解决；65～90为26个大写英文字母，97～122号为26个小写英文字母；

 

public class Solution {
    public int FirstNotRepeatingChar(String str) {
        if(str==null||str.length()==0) return -1;
        int[] count = new int[123];//默认是0
        for(int i=0;i<str.length();i++){
            count[str.charAt(i)]++;
        }
        for(int i=0;i<str.length();i++){
            if(count[str.charAt(i)]==1){
                return i;
            }
        }
        return 0;
    }
}

 

 

 

题三：【数组中的逆序对】

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

【输入描述】题目保证输入的数组中没有的相同的数字，数据范围：对于%50的数据,size<=10^4；对于%75的数据,size<=10^5；对于%100的数据,size<=2*10^5；

【示例】输入：1,2,3,4,5,6,7,0     输出：7

分析：暴力解决时间复杂度太高O(N^2)；采用分治的思想，将数组不断一分为二，再合并排序，在合并排序的过程中，判断是否是逆序对。

 

 归并排序：【图解】 　　　　　　　　　　　　　　　　　　　　　　　　　　【合并】

 

 

 

 

 

 

 

 

 

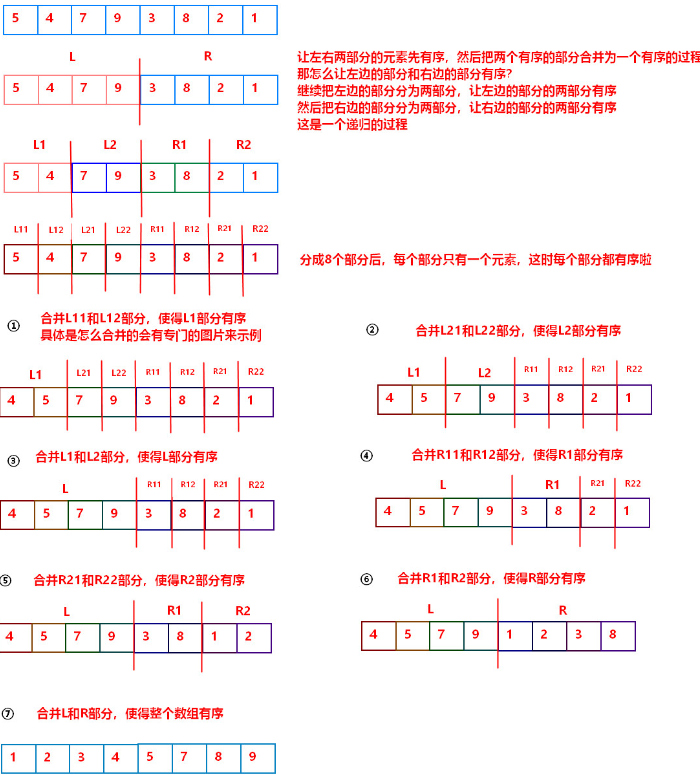
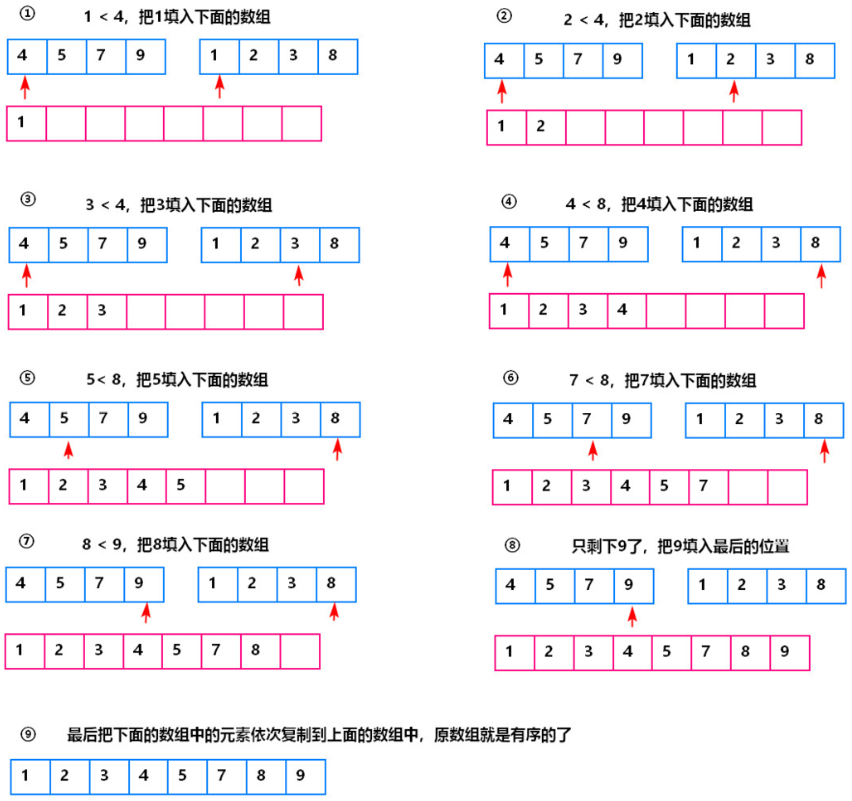
题

 

 

 

 

 

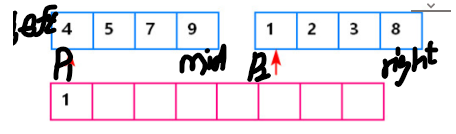
 【注意】： count=count+mid-p1+1；//当左边有序小数组p1指向的元素大于p2指向的元素，这就说明p1~mid范围内的元素（有序，mid-p1+1）都大于p2指向的元素，所以有mid-p1+1个逆序对。例如下图，array[p1]=4  >  array[p2]=1,这就是说p1~mid，即4、5、7、9都大于1，有mid-p1+1=3-0+1=4个。

public class Solution {
    private int count=0;//计数
    private final int k = 1000000007;
    public int InversePairs(int [] array) {
        mergeSort(array,0,array.length-1);
        return count;
    }
    //分解
    public void mergeSort(int[] array, int left, int right){
        if(left>=right) return;
        int mid = (left+right)/2;
        mergeSort(array,left,mid);
        mergeSort(array,mid+1,right);
        merge(array,left,mid,right);
    }
    //合并
    public void merge(int[] array, int left, int mid, int right){
       //建立两个指针P1，P2
        int p1 = left;//第一个分数组开头
        int p2 = mid+1;//第二个分数组开头
        int i=0;
        int[] temp = new int[right-left+1];
        while(p1<=mid&&p2<=right){
            if(array[p1]<=array[p2]){
                temp[i++] = array[p1++];
            }else{
                temp[i++] = array[p2++];
                count = (count+mid-p1+1)%k;
            }
        }
        while(p1<=mid){
            temp[i++]=array[p1++];
        }
        while(p2<=right){
            temp[i++]=array[p2++];
        }
        for(int j=0;j<temp.length;j++){
            array[left+j]=temp[j];
        }
    }
}

 

四：【两个链表的第一个公共结点】

 输入两个链表，找出它们的第一个公共结点。

分析：公共节点，即两个结点相同（p1.val=p2.val并且p1.next=p2.next）。因此，如果有公共节点，那么就会有相同的尾部。

 

 

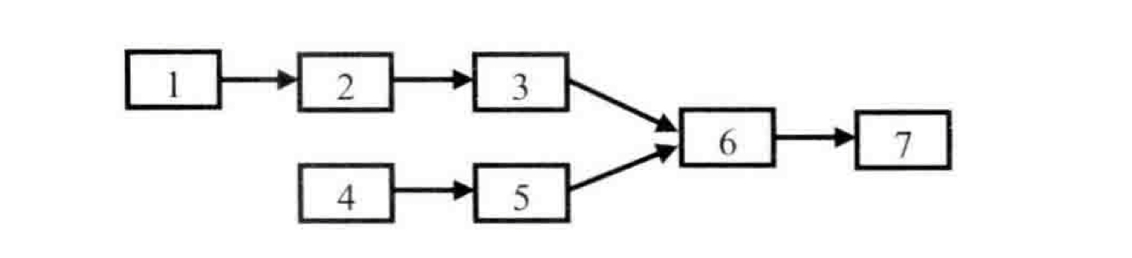
法一：暴力，循环嵌套 O(m*n)；m是pHead1长度，n是pHead2长度。

法二：从尾部向后遍历，遍历的最后一个公共节点就是我们想要的，但是题目中给的是单向链表，先进后出=》使用队列存放公共节点，当p1!=p2时，则两个队列头（相等）就是我们想要的。时间和空间复杂度都是O(m+n)。

法三：首先遍历两个链表的长度，计算长的比短的长多少（k），先让长的链表先走k步，然后再同时遍历两个链表找到公共节点。时间复杂度O(m) ，m是较长链表的长度，空间复杂度O(1)。

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        if(pHead1==null||pHead2==null) return null;
        int i = 0;//第一个链表长度
        int j = 0;//第二个链表长度
        ListNode head1 = pHead1;
        ListNode head2 = pHead2;
        //计算两链表长度
        while(head1!=null){
            i++;
            head1=head1.next;
        }
        while(head2!=null){
            j++;
            head2=head2.next;
        }
        if((i-j)>=0){
            return fingCommonNode(pHead1,pHead2,i-j);
        }else{
            return fingCommonNode(pHead2,pHead1,j-i);
        }
    }
    public ListNode fingCommonNode(ListNode pHead1, ListNode pHead2, int k){
        while(k>0){
            pHead1 = pHead1.next;
            k--;
        }
        while(pHead1!=null){
            if(pHead1==pHead2) return pHead1;
            pHead1=pHead1.next;
            pHead2=pHead2.next;
        }
        return null;
    }
}